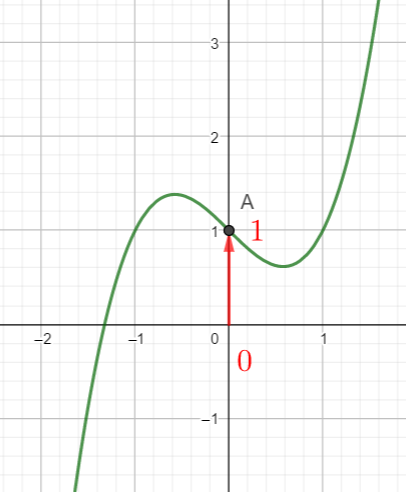
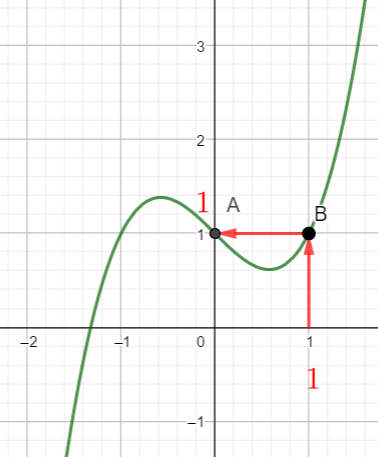
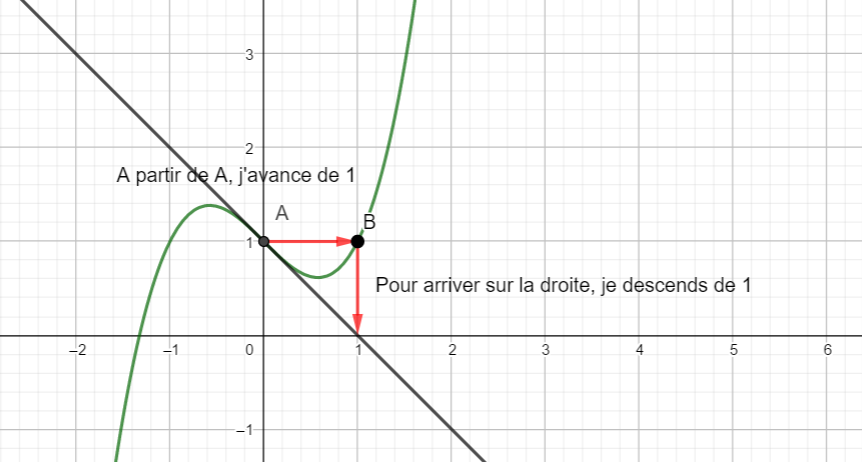
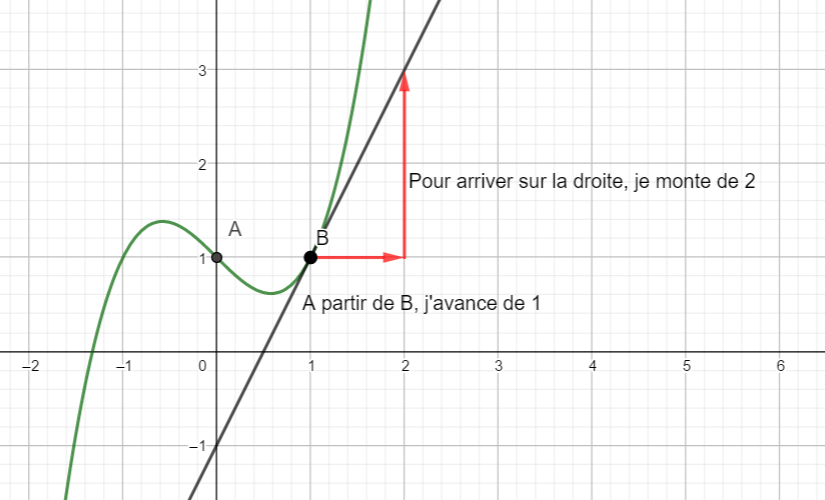
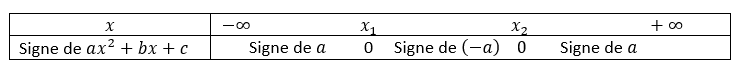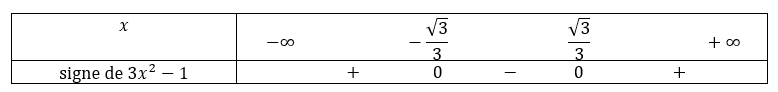Exercice niveau 1ère type évaluation fin d’année sur les fonctions sur la page Facebook

ANALYSE, Dérivation, Exercices type dérivation, Niveau première

Dans la figure ci-dessous, on a tracé $C_f$ , la courbe représentative d’une fonction $f$ définie et
dérivable sur $\mathbf{R}$ ainsi que les tangentes à $C_f$ aux points $A$ d’abscisse $0$ et $B$ d’abscisse $1$ .

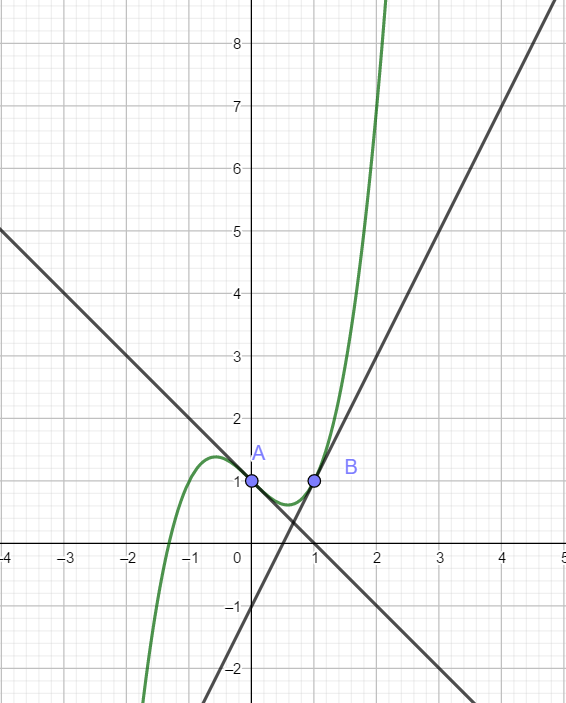
Compléter le tableau de valeurs ci-dessous à l’aide de la courbe ci-dessus.

$x$	$0$	$1$
$f(x)$
$f'(x)$

On admet que la fonction 𝑓 est définie sur $\mathbf{R}$ par :
$f(x)=x^3-x+1$ .
2. a. Calculer $f'(x)$ .

b. Résoudre dans $\mathbf{R}$ l’équation : $f'(x) \geq 0$ .

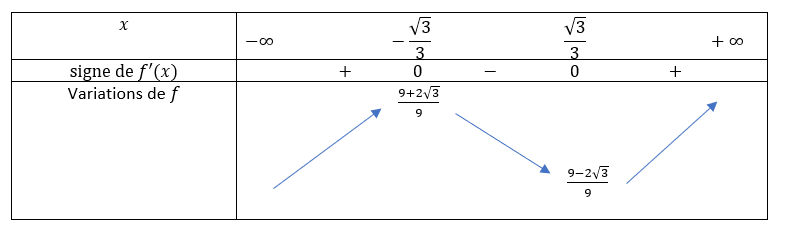
3. Dresser le tableau de variations de la fonction $f$ sur $\mathbf{R}$ .

4. Le point $C(1;5)$ appartient-il à la tangente à la courbe représentative de 𝑓 au point
d’abscisse $-1$ ?

$f(x)$ est	$f'(x)$ se calcule ainsi :
une somme $u+v$	$u’+v’$
le produit d’une constante $k$ par une fonction $u$ c’est-à-dire $ku$	$k\times u’$
un produit de deux fonctions $u\times v$	$u’\times v+u\times v’$
l’inverse d’une fonction $\frac{1}{u}$	$-\frac{u’}{u^2}$
un quotient $\frac{u}{v}$	$\frac{u’\times v-u\times v’}{v^2}$

Fonction	$f(x)$	Dérivable sur…	$f'(x)$
constante	$f(x)=k$	$\mathbf{R}$	$f'(x)=0$
identité	$f(x)=x$	$\mathbf{R}$	$f'(x)=1$
carré	$f(x)=x^2$	$\mathbf{R}$	$f'(x)=2x$
cube	$f(x)=x^3$	$\mathbf{R}$	$f'(x)=3x^2$
inverse	$f(x)=\frac{1}{x}$	$\left]-\infty;0\right[\cup\left]0;+\infty\right[$	$f'(x)=-\frac{1}{x^2}$
racine carrée	$f(x)=\sqrt{x}$	$]0;+\infty[$	$f'(x)=\frac{1}{2\sqrt{x}}$