Vous pouvez revoir ce qui a été fait l’an passé en cliquant sur Spécialité 1ère puis ALGEBRE puis Les suites dans la page d’accueil de Math’O Karé.
Sommaire
Activité d’approche pour les limites de suites
suite n°1
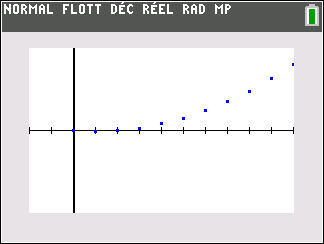
soit (u_n) la suite définie sur \mathbf{N} par u_n=3n-1.
On s’intéresse au comportement de la suite (u_n) lorsque les valeurs de n deviennent très grandes.
Voici deux façons d’observer le comportement de la suite (u_n) à l’aide de la calculatrice TI-83 Premium CE Python.
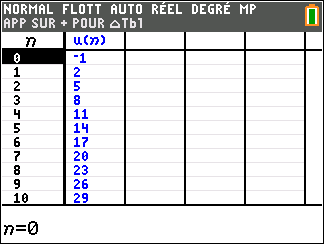
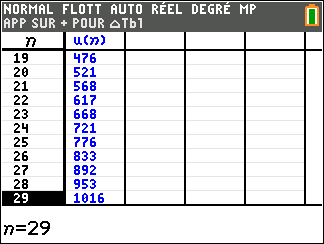
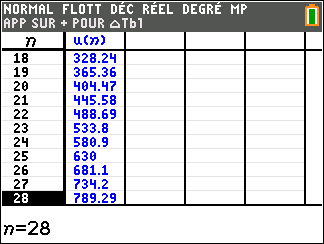
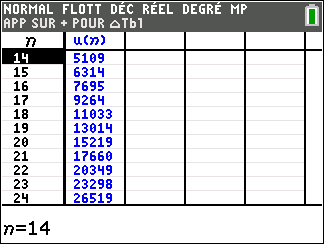
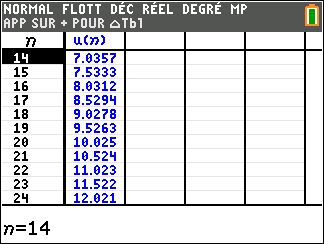
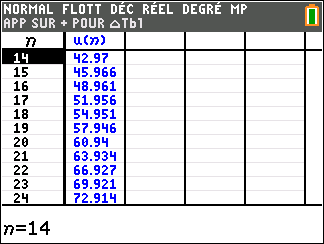
Pour étudier le comportement de la suite (u_n) lorsque les valeurs de n deviennent très grandes, il faudrait descendre dans le tableau mais c’est long. Mieux vaut utiliser une feuille Excel comme c’est proposé plus bas.
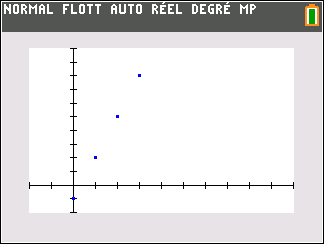
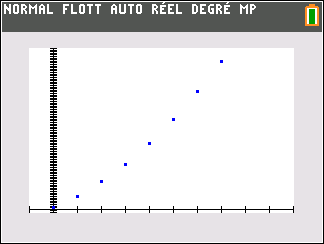
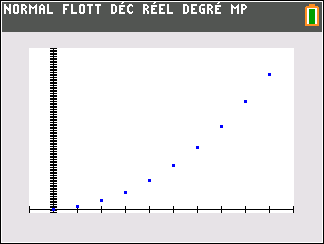
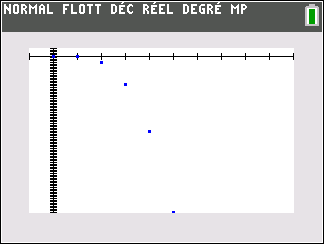
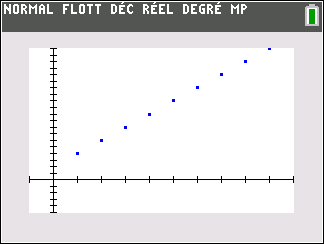
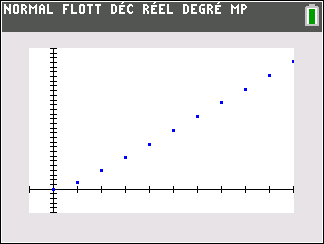
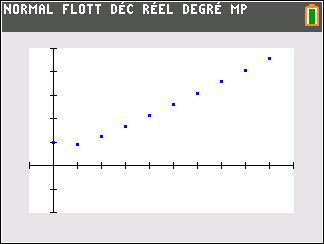
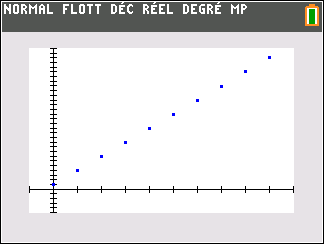
Le nuage de points de coordonnées (n;u_n) ci-dessus ne permet pas vraiment de faire une conjecture. Il faudrait pouvoir observer pour des grandes valeurs de n.
Mieux vaut utiliser le nuage de points Excel comme c’est proposé plus bas
En utilisant une feuille de calcul Excel, on peut générer les termes de la suite plus rapidement qu’avec la calculatrice et observer ce qui se passe pour de grandes valeurs de n
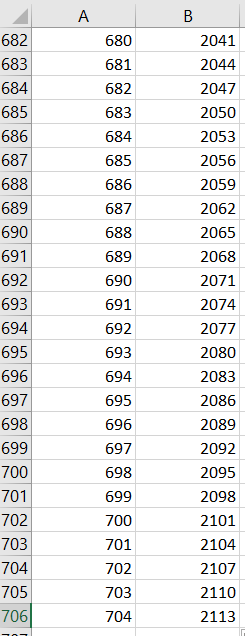
En lisant le tableau ci-dessus, il semble que quand les n dans la colonne de gauche deviennent de plus en plus grands, les (u_n) dans la colonne de droite deviennent aussi de plus en plus grands.
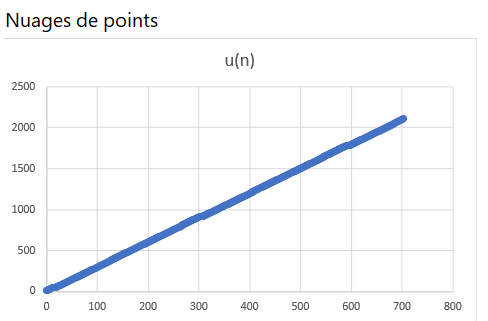
En observant le nuage de points de coordonnées (n;u_n) ci-dessus, il semble que quand les n deviennent de plus en plus grands, les (u_n) deviennent aussi de plus en plus grands.
On écrit \lim_{n \to {+\infty}} u_n = +\infty
suite n°2
soit (u_n) la suite définie sur \mathbf{N} par u_n=-2n+5.
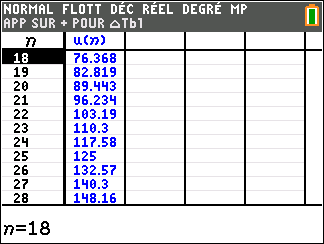
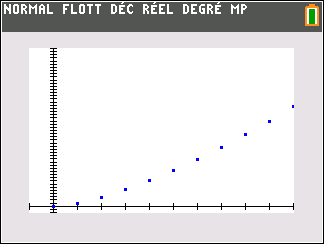
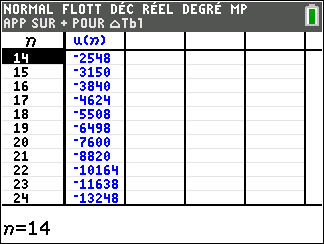
Voici deux façons de la représenter à l’aide de la calculatrice TI-83 Premium CE Python.

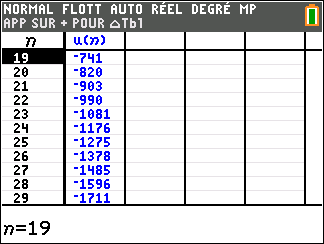
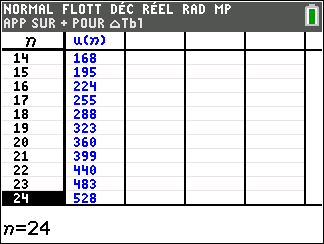
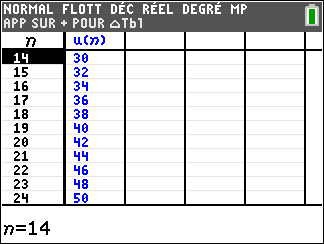
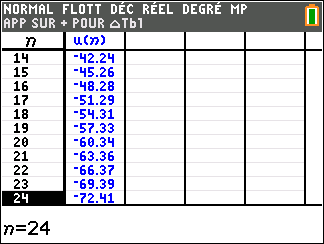
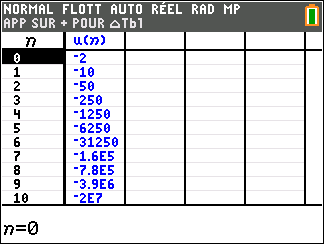
Pour étudier le comportement de la suite (u_n) lorsque les valeurs de n deviennent très grandes, il faudrait descendre dans le tableau mais c’est long. Mieux vaut utiliser une feuille Excel comme c’est proposé plus bas.
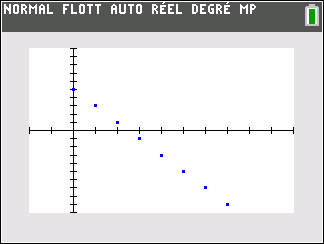
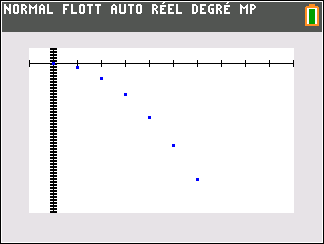
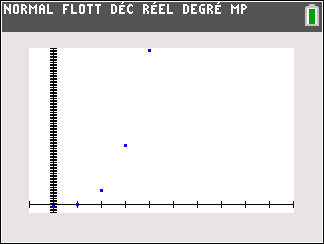
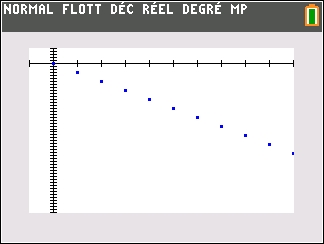
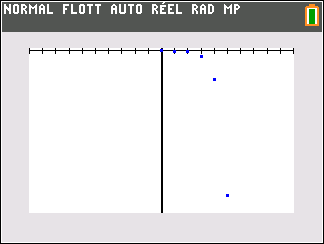
Le nuage de points de coordonnées (n;u_n) ci-dessus ne permet pas vraiment de faire une conjecture. Il faudrait pouvoir observer pour des grandes valeurs de n.
Mieux vaut utiliser le nuage de points Excel comme c’est proposé plus bas
En utilisant une feuille de calcul Excel, on peut générer les termes de la suite plus rapidement qu’avec la calculatrice et observer ce qui se passe pour de grandes valeurs de n

En lisant le tableau ci-dessus, il semble que quand les n dans la colonne de gauche deviennent de plus en plus grands, les (u_n) dans la colonne de droite deviennent aussi de plus en plus petits.
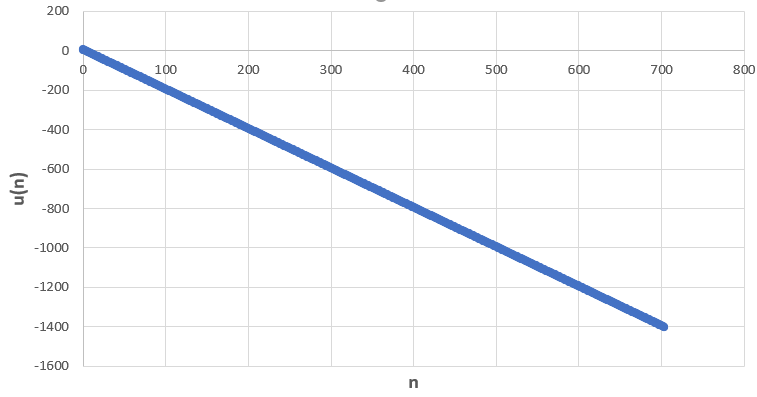
En observant le nuage de points de coordonnées (n;u_n) ci-dessus, il semble que quand les n deviennent de plus en plus grands, les (u_n) deviennent aussi de plus en plus petits.
On écrit \lim_{n \to {+\infty}} u_n = -\infty
suite n°3 : soit (u_n) la suite définie sur \mathbf{N}^{*} par u_n=\frac{1}{n}+2.
Voici deux façons de la représenter à l’aide de la calculatrice TI-83 Premium CE Python.
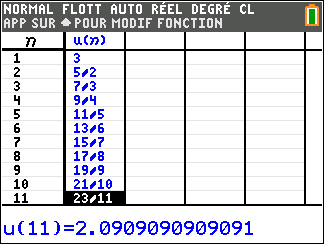
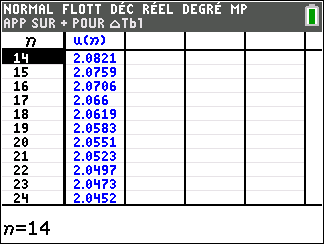
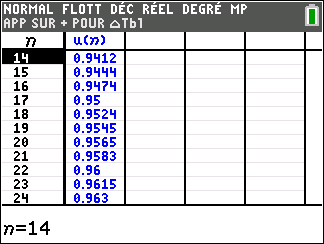
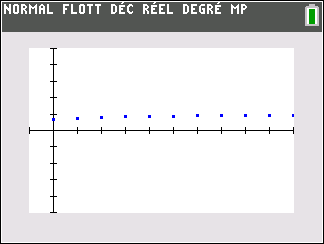
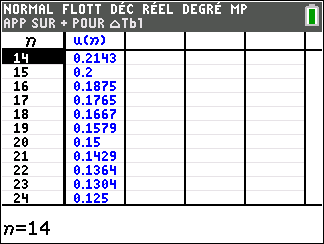
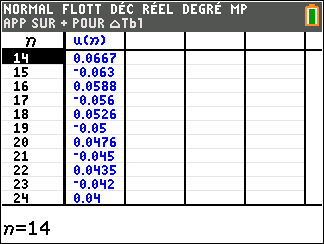
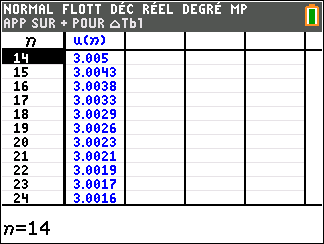
Pour étudier le comportement de la suite (u_n) lorsque les valeurs de n deviennent très grandes, il faudrait descendre dans le tableau . On observe que les valeurs de (u_n) semblent rapidement se rapprocher de la valeur 2.
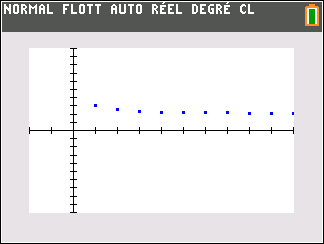
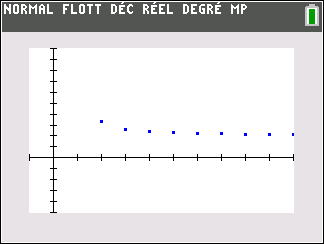
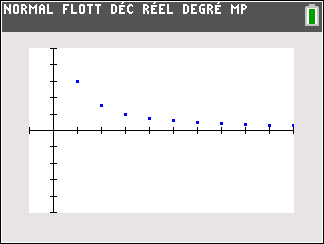
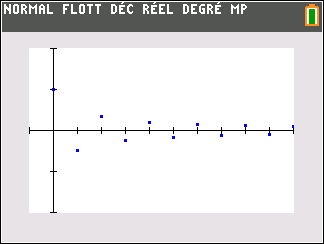
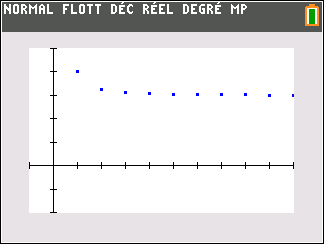
Le nuage de points de coordonnées (n;u_n) ci-dessus ne permet de faire une conjecture. Il semble que les valeurs de u_n se rapprochent assez vite de la valeur 2.
On écrit \lim_{n \to {+\infty}} u_n = 2
suite n°4 : soit (u_n) la suite définie sur \mathbf{N} par u_n=(-1)^n.
Voici deux façons de la représenter à l’aide de la calculatrice TI-83 Premium CE Python.
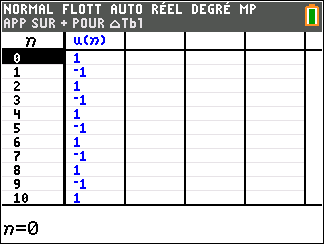
Pour étudier le comportement de la suite (u_n) lorsque les valeurs de n deviennent très grandes, il faudrait descendre dans le tableau . On observe que les valeurs de (u_n) ne se rapprochent pas d’une valeur.
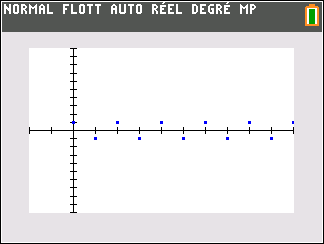
Le nuage de points de coordonnées (n;u_n) ci-dessus permet de dire que les valeurs de u_n ne se rapprochent pas d’une valeur donnée.
On dit que la suite u_n n’admet pas de limite.
Propriétés : limites des suites de référence
Propriété n°1 (admise)
Les suites de terme général \frac{1}{n} , \frac{1}{n^2} , \frac{1}{n^3} ,…, \frac{1}{n^k} ( k entier naturel) et \frac{1}{\sqrt{n}} tendent vers 0 quand n tend vers +\infty .
Définition
On dit qu’une suite de terme général u_n est convergente lorsqu’elle admet une limite finie l quand n tend vers +\infty ( c’est le cas des suites de la propriété n°1)
Illustration avec le mode graph de la TI-83
la suite de terme général \frac{1}{n}
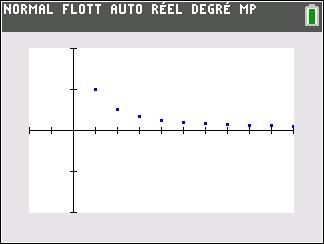
\lim_{n \to {+\infty}} \frac{1}{n} = 0
la suite de terme général \frac{1}{n^2}
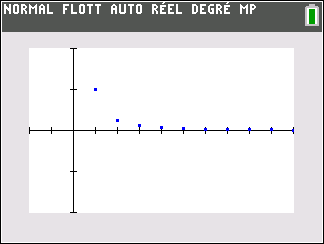
\lim_{n \to {+\infty}} \frac{1}{n^2} = 0
la suite de terme général \frac{1}{n^3}
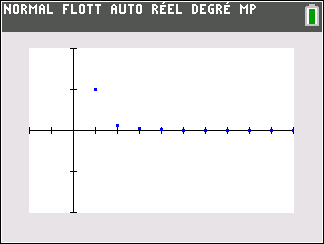
\lim_{n \to {+\infty}} \frac{1}{n^3} = 0
la suite de terme général \frac{1}{\sqrt{n}}
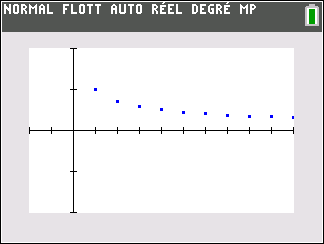
\lim_{n \to {+\infty}} \frac{1}{\sqrt{n}}= 0
Propriété n°2 (admise)
Les suites de terme général n, n^2, n^3,…, n^k ( k entier naturel) et \sqrt{n} tendent vers +\infty quand n tend vers +\infty .
Définition
On dit qu’une suite de terme général u_n est divergente lorsqu’elle n’est pas convergente. C’est le cas quand la suite admet une limite infinie ou quand la suite n’admet pas de limite.
Illustration avec le mode graph de la TI-83
la suite de terme général n
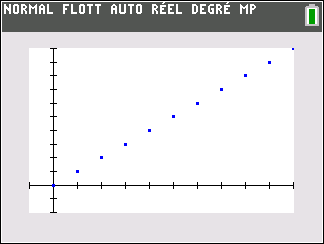
\lim_{n \to {+\infty}} n = +\infty
la suite de terme général n^2
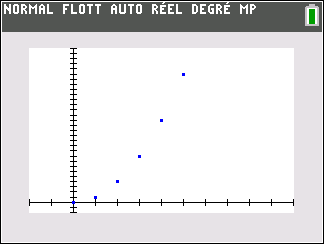
\lim_{n \to {+\infty}} n^2 = +\infty
la suite de terme général n^3
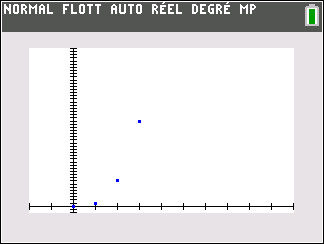
\lim_{n \to {+\infty}} n^3 = +\infty
Propriétés : limites et opérations
Dans les tableaux ci-dessous, les lettres l et l’ représentent des nombres réels.
| \lim_{n\to{+\infty}}u_n= | l | l | l | +\infty | -\infty | +\infty |
| \lim_{n\to{+\infty}}v_n= | l’ | +\infty | -\infty | +\infty | -\infty | -\infty |
| \lim_{n\to{+\infty}}u_n+v_n= | l+l’ | +\infty | -\infty | +\infty | -\infty | Forme indéterminée |
Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.
| \lim_{n\to{+\infty}} u_n= | l | l\ne0 | \infty | 0 |
| \lim_{n\to{+\infty}} v_n= | l’ | \infty | \infty | \infty |
| \lim_{n\to{+\infty}} u_nv_n= | l\times l’ | \infty | \infty | Forme indéterminée |
Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.
Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer la règle des signes pour conclure.
| \lim_{n\to{+\infty}}u_n= | l | l\ne0 | l | \infty | \infty | 0 |
| \lim_{n\to{+\infty}}v_n= | l’\ne0 | 0 | \infty | l | \infty | 0 |
| \lim_{n\to{+\infty}}\frac{u_n}{v_n}= | \frac{l}{l’} | \infty | 0 | \infty | Forme indéterminée | Forme indéterminée |
Remarque
quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .
Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer la règle des signes pour conclure.
Exercice n°1 (le terme général est une somme )
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=n^2+6n+1
2. u_n=-2n^2-n
3.u_n=n^2+\sqrt{n}
4.u_n=n^2-2n
Exercice n°2 ( le terme général est un produit )
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=n\sqrt{n}
2. u_n=n^2(1-n)
3.u_n=(-2n^2-1)(1-n)
4.u_n=2n^2(\frac{1}{n}+\frac{1}{n^2})
Exercice n°3 ( le terme général est un quotient )
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{2+\frac{1}{n}}{1-\frac{1}{n^2}} pour n\geq 2
2. u_n=\frac{2+n}{3-n} pour n\geq 4
3.u_n=\frac{3n}{n^2+1} pour n\geq 1
4.u_n=\frac{2n^2}{n+1} pour n\in \mathbf{N}
Propriétés : limites et comparaisons
Propriété n°3
Soient deux suites (u_n) et (v_n) telles qu’à partir d’un certain rang, u_n\leq v_n,
Si \lim_{n \to {+\infty}}u_n=+\infty alors \lim_{n \to {+\infty}}v_n=+\infty
Si \lim_{n \to {+\infty}}v_n=-\infty alors \lim_{n \to {+\infty}}u_n=-\infty
Exercice n°4
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=-\frac{n}{2}+\sqrt{n^2+1} pour n\in \mathbf{N}. On montrera que u_n\geq \frac{n}{2}.
2. u_n=3n+cos(n) pour n\in \mathbf{N}. On montrera que u_n\geq 3n-1.
3.u_n=-3n-sin(n) pour n\in \mathbf{N}. On montrera que u_n\leq 1-3n.
Propriété n°4
Soient deux suites (u_n) et (v_n) qui convergent respectivement vers l et l’.
On suppose qu’à partir d’un certain rang, u_n\leq v_n.
Alors l \leq l’
Théorème des gendarmes
Soient trois suites (u_n), (v_n) et (w_n) telles qu’à partir d’un certain rang, u_n\leq v_n\leq w_n.
Si les suites (u_n) et (w_n) convergent vers l alors la suite (v_n) converge vers l.
Exercice n°5
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{(-1)^n}{n+1} pour n\in \mathbf{N}. On montrera que \frac{-1}{n+1}\leq u_n\leq \frac{1}{n+1}.
2. u_n=3+\frac{cos(n)}{n^2} pour n\geq 1. On montrera que 3-\frac{1}{n^2}\leq u_n\leq 3+\frac{1}{n^2}.
Suites géométriques, suites monotones.
Suites du type q^n
Propriété n°5
Soit q un nombre réel.
- Si q \leq -1 alors la suite (q^n) diverge et n’admet pas de limite.
- Si -1<q<1 alors la suite (q^n) converge vers 0.
- Si q =1 alors la suite (q^n) converge vers 1.
- Si q >1 alors la suite (q^n) diverge vers +\infty.
Exercice n°6
Déterminer la limite de la suite (u_n) dans chaque cas lorsque c’est possible.
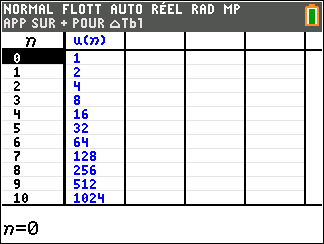
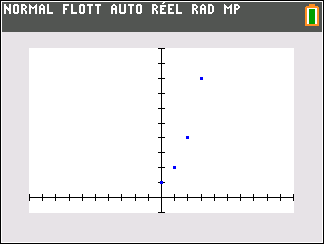
- (u_n) est une suite géométrique de raison 2 et de premier terme u_0=1.
2. (u_n) est une suite géométrique de raison 5 et de premier terme u_0=-2
3.(u_n) est une suite géométrique de raison 0.1 et de premier terme u_0=5
4.(u_n) est une suite géométrique de raison -2 et de premier terme u_0=3
Suites monotones
Propriété n°6
- Toute suite croissante majorée converge.
- Toute suite décroissante minorée converge.
- Toute suite croissante non majorée diverge vers +\infty.
- Toute suite décroissante non minorée diverge vers -\infty.
Exercice n°7
Soit la suite (u_n) définie par u_n=\frac{n}{n+1} pour n\in \mathbf{N}.
- Montrer que u_n est majorée par 1.
2. Montrer que (u_n) est croissante.
3. En déduire que la suite (u_n) converge.
Exercice n°8
Soit la suite (u_n) définie par u_n=\frac{-2n+1}{n+3} pour n\in \mathbf{N}.
- Montrer que u_n est minorée par -2.
2. Montrer que (u_n) est décroissante.
Comme \frac{-2n+1}{n+3} est négatif à partir du rang 1, on ne peut pas appliquer la méthode n°2 vue en première. C’est à dire comparer \frac{u_{n+1}}{u_n} à 1.
3. En déduire que la suite (u_n) converge.