On s’intéresse à une population de tortues vivant sur une île et dont le nombre d’individus diminue de façon inquiétante.
Au début de l’an 2000, on comptait 300 tortues. Une étude a permis de modéliser ce nombre de
tortues par la suite (u_n) définie par : u_0=0.3 et u_{n+1}=0.9u_{n}(1-u_n)
où pour tout entier naturel n, u_n représente le nombre de tortues, en milliers, au début de l’année 2000+n.
Partie A : avec un tableur.
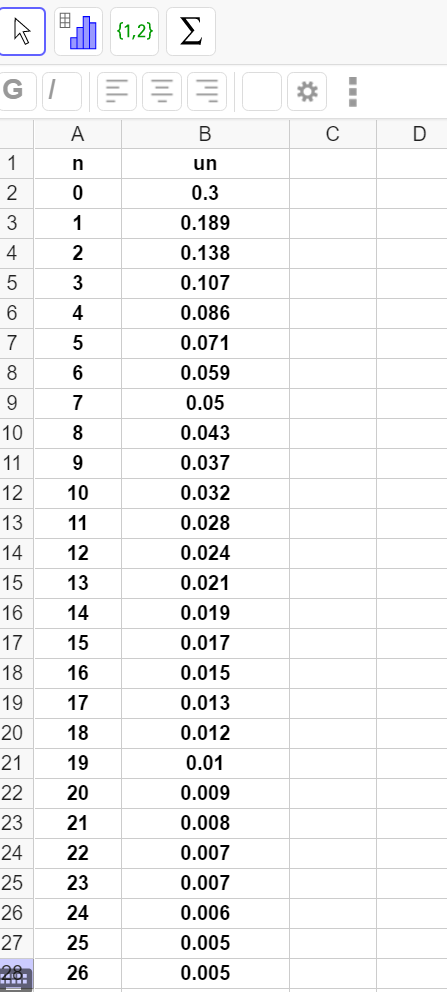
- Saisir la bonne formule dans la cellule B3 et la copier vers le bas pour générer les termes de la suite (u_n).
2. A l’aide du tableur obtenu à la question précédente, conjecturer la limite de la suite (u_n).
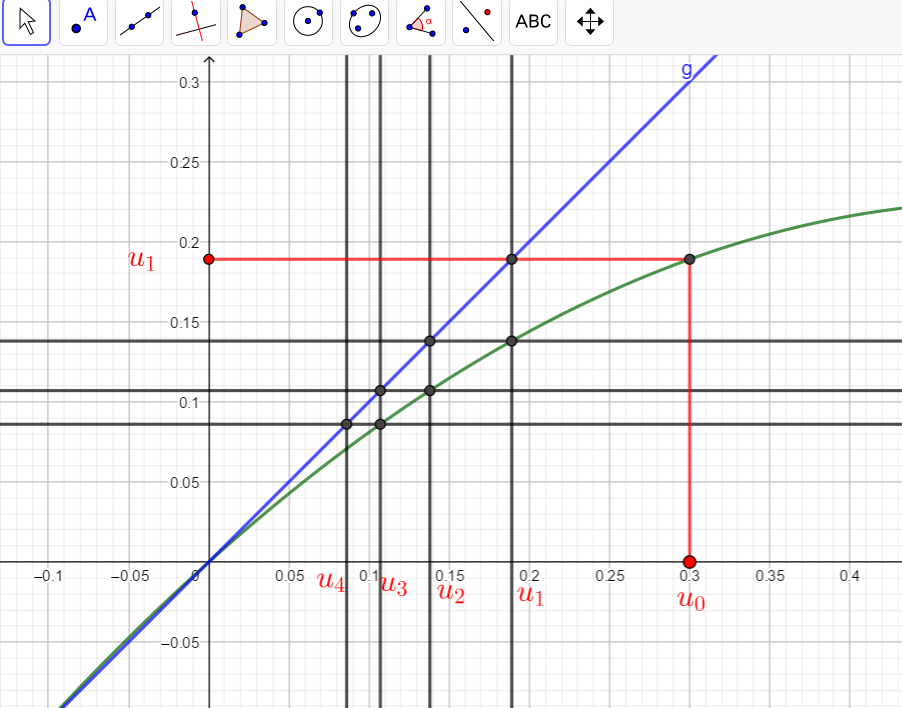
Partie B : avec la courbe de la fonction f(x)=0.9x(1-x) et la droite d’équation y=x.
- Placer de façon géométrique à l’aide des courbes ci-dessous, les termes u_{1}, u_{2}, u_{3} et u_{4} sur l’axe des abscisses.
Partie C : avec le calcul.
- On admet que, pour tout entier naturel n, u_{n} et 1-u_{n} appartiennent à l’intervalle ]0;1[.
Montrer que, pour tout entier naturel n, 0< u_{n+1}< 0.9 u_n.
2. Montrer que, pour tout entier naturel n, 0\leq u_{n}\leq 0.3\times 0.9^n.
3. Déterminer la limite de la suite (u_n). Que peut-on en conclure sur l’avenir de cette population de tortues ?