Sommaire
Exercice n°1 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=2n^2+n+5
2. u_n=-n^2-3n
3.u_n=2n^2+3\sqrt{n}
4.u_n=-n^2+2n
Exercice n°2 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=n^2\sqrt{n}
2. u_n=n^3(1-2n)
3.u_n=(-n^2+1)(1-2n)
4.u_n=n^2(\frac{2}{n}-\frac{3}{n^2})
Exercice n°3 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{4+\frac{1}{n}}{2-\frac{1}{n^2}} pour n\geq 1
2. u_n=\frac{6+n}{2+n} pour n\in \mathbf{N}
3.u_n=\frac{n}{n^3+1} pour n\in \mathbf{N}
4.u_n=\frac{5n^2}{2n+1} pour n\in \mathbf{N}
Exercice n°4 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{n}{2}-\sqrt{n^2+1} pour n\in \mathbf{N}. On montrera que u_n\leq – \frac{n}{2}.
2. u_n=2n+cos(n) pour n\in \mathbf{N}. On montrera que u_n\geq 2n+1.
3.u_n=-n^2+sin(n) pour n\in \mathbf{N}. On montrera que u_n\leq -n^2+1.
Exercice n°5 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{(-1)^n}{n^2} pour n\in \mathbf{N}. On montrera que \frac{-1}{n^2}\leq u_n\leq \frac{1}{n^2}.
2. u_n=2-\frac{sin(n)}{n} pour n\geq 1. On montrera que 2-\frac{1}{n}\leq u_n\leq 2+\frac{1}{n}.
Exercice n°6 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas.
- u_n=\frac{(-1)^n}{n+1} pour n\in \mathbf{N}. On montrera que \frac{-1}{n+1}\leq u_n\leq \frac{1}{n+1}.
2. u_n=3+\frac{cos(n)}{n^2} pour n\geq 1. On montrera que 3-\frac{1}{n^2}\leq u_n\leq 3+\frac{1}{n^2}.
Exercice n°7 (calcul de limites)
Déterminer la limite de la suite (u_n) dans chaque cas lorsque c’est possible.
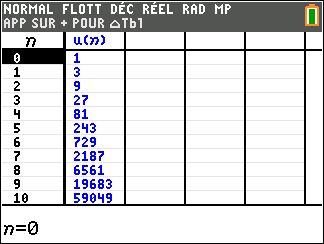
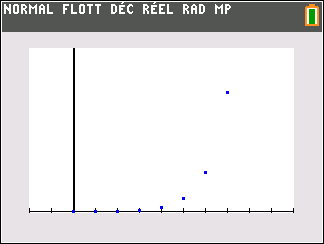
- (u_n) est une suite géométrique de raison 3 et de premier terme u_0=1.
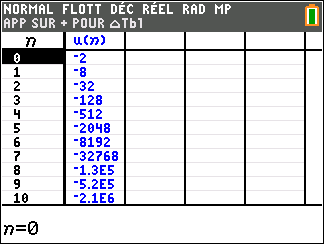
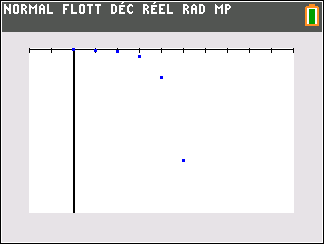
2. (u_n) est une suite géométrique de raison 4 et de premier terme u_0=-2
3.(u_n) est une suite géométrique de raison 0.2 et de premier terme u_0=10
4.(u_n) est une suite géométrique de raison -3 et de premier terme u_0=2
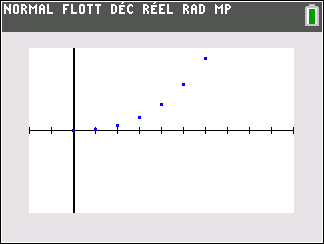
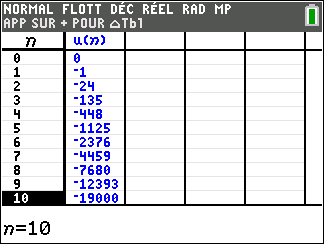
Exercice n°8 (algorithme, tableur, calcul de limites)
Actuellement le taux de mortalité des abeilles est de 30 % par an en moyenne en France.
Un apiculteur possède 200 colonies et compte-tenu du taux de mortalité, il décide de rajouter 42 colonies chaque année pour essayer de stabiliser sa production.
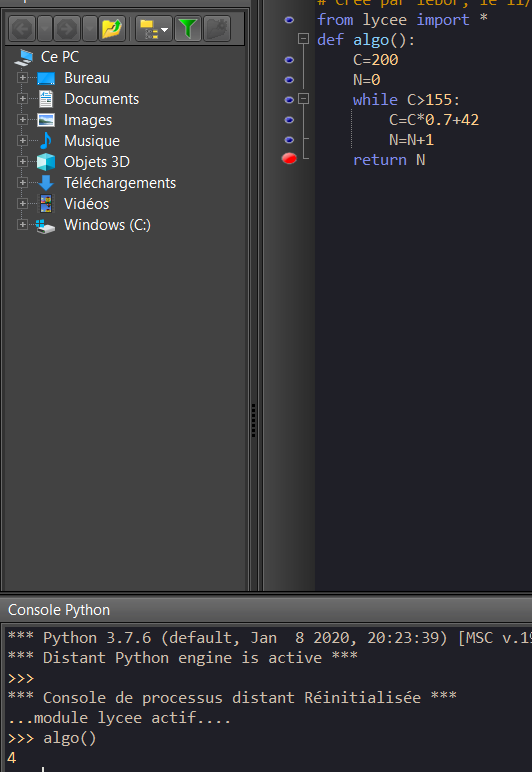
- On donne le programme suivant écrit en langage Python :

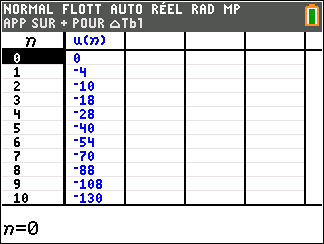
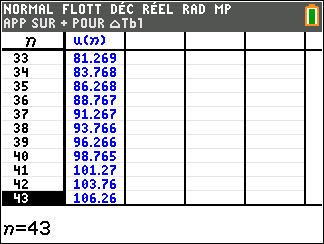
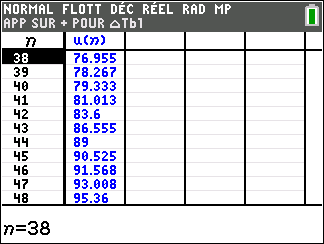
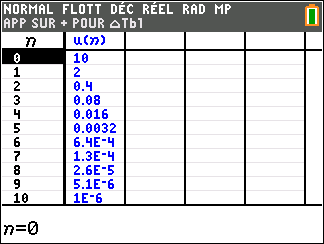
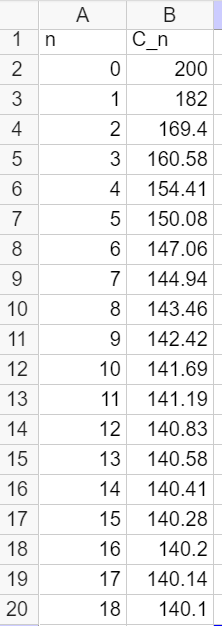
a. Faire tourner le programme à la main et compléter le tableau ci-dessous ( arrondir les valeurs C à l’unité près )

b. Quelle est la valeur de N renvoyée par le programme ? Interpréter ce résultat dans le contexte de l’exercice.
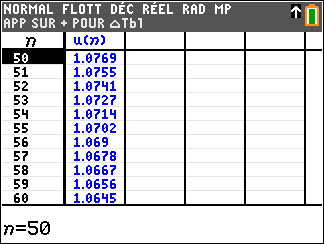
On note C_n le nombre de colonies d’abeilles au début de la nième année .
On a alors C_0=200.
On admet que pour tout entier n,
C_{n+1}=0.7C_n+42.
2. La suite C_n est-elle arithmétique ? La suite C_n est-elle géométrique ?
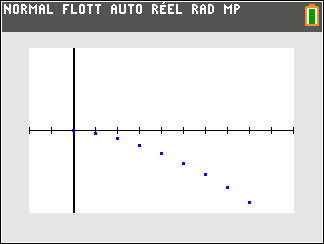
3. On admet que C_n=60\times 0.7^n+140. L’apiculteur pourra-t-il espérer atteindre les 150 colonies dans le futur ? Vous pourrez utiliser la page géogébra ci-dessous en saisissant la bonne formule dans la cellule B2.
4. Calculer lim_{n\to +\infty}C_n. Interpréter le résultat dans le cadre de l’exercice.
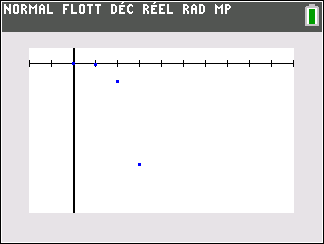
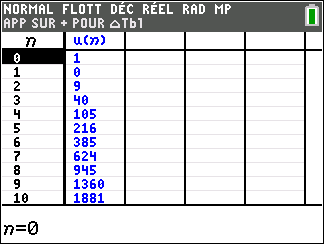
Exercice n°9 (suite géométrique, calcul de limites)
Dans un laboratoire, on cultive des bactéries artificielles.
Le premier jour de l’étude, la culture compte 6000 cellules.
Un test mené sur cette culture prouve que 15 % des cellules disparaissent chaque jour. On décide alors d’ajouter 3000 cellules chaque jour dans la culture.
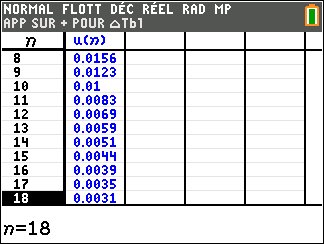
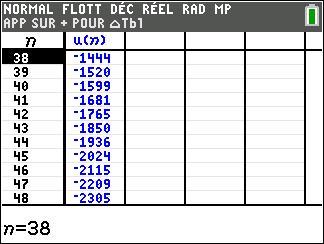
On note u_n le nombre de bactéries présentes dans la culture le jour n. On a alors u_0=6000.
1.a.Calculer u_{1} et u_{2}.
1.b. Montrer que la suite u_n n’est ni géométrique, ni arithmétique.
On admet dans la suite de l’exercice que u_{n+1}=0.85\times u_n+3000
2. On considère la suite v_n définie par v_{n}=u_n-20000.
a. Calculer v_0 et démontrer que la suite (v_n) est géométrique de raison 0.85 .
b. Pour tout entier naturel n, exprimer v_n en fonction de n puis montrer que u_n=-14000\times 0.85^n+20000
3. Est-il correct d’affirmer que le nombre de bactéries contenues dans la culture aura triplé au bout de 4 semaines ?
4. Calculer lim_{n\to +\infty} u_n. Interpréter le résultat dans le contexte de l’exercice.
Exercice n°10 (algorithme, suite géométrique, calcul de limites)
Un pays compte 300 loups en 2017. On estime que la population des loups croit naturellement au
rythme de 12 % par an. Pour réguler la population des loups. le gouvernement autorise les chasseurs
à tuer un quota de 18 loups par an.
On modélise la population par une suite (u_n) le terme u_n représentant le nombre de loups de ce pays
en 2017+n.
- a. Avec ce modèle vérifier que le nombre de loups de ce pays en 2018 sera de 318.
b. Justifier que, pour tout entier n \in \mathbf{N} , u_{n+1}=1.12u_n-18.
2. Recopier et compléter l’algorithme suivant pour qu’il détermine au bout de combien d’années
la population de loups aura doublé.
N ← 0
U ← 300
Tant que ………………… faire
U ← ···
N ← ···
Fin Tant que
3. On définit la suite (v_n) par : v_n=u_n-150 pour tout n\in\mathbf{N}.
a. Montrer que la suite (v_n) est une suite géométrique de raison 1.12.
Préciser son terme initial.
b. Exprimer, pour tout n\in\mathbf{N}, v_n en fonction de n.
En déduire u_n en fonction de n.
c. Quelle est la limite de la suite (u_n)? Justifier.
Que peut-on en déduire ?
Exercice n°11 : ( tableur, démonstration par récurrence, suite croissante, calcul de limites)
On considère deux suites (u_n) et (v_n) :
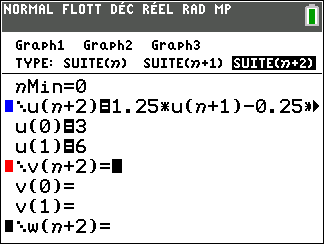
• la suite (u_n) définie par u_0=1et pour tout entier naturel n , u_{n+1}=2u_n-n+3
• la suite (v_n) définie, pour tout entier naturel n, par v_n=2^n
Partie A : Conjectures
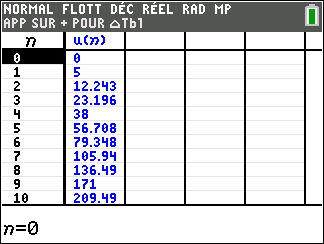
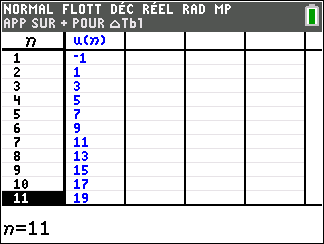
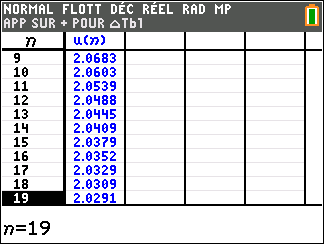
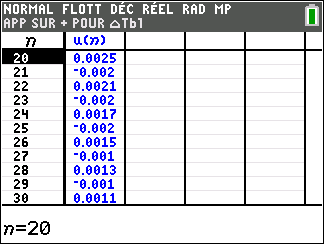
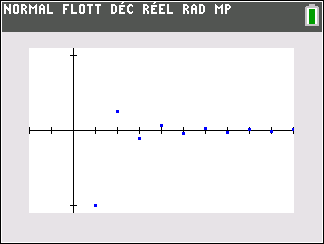
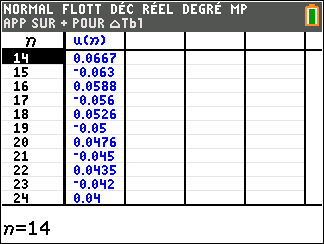
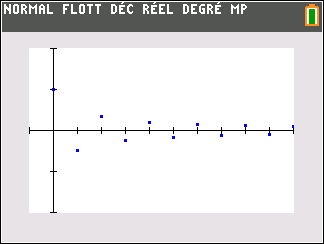
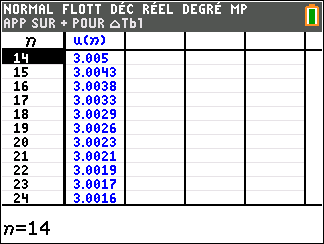
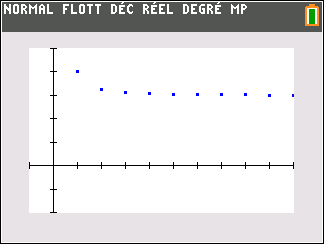
1. Dans la fenêtre active Géogébra ci-dessous, saisir les formules adéquates dans les cellules B3, C2 et D2 et les tirer vers le bas pour générer les termes des trois suites (u_n) , (v_n) et (\frac{u_n}{v_n}).
2. Conjecturer les limites des suites (u_n) et (\frac{u_n}{v_n})
Partie B : Étude de la suite (u_n)
1. Démontrer par récurrence que, pour tout entier naturel n, on a
u_n=3\times 2^n+n-2.
2. Déterminer la limite de la suite (u_n).
Partie C: Étude de la suite (\frac{u_n}{v_n})
1. Démontrer que la suite (\frac{u_n}{v_n}) est décroissante à partir du rang 3.
2. On admet que, pour tout entier n supérieur ou égal à 4, on a : 0<\frac{n}{2^n}\leq \frac{1}{n}.
Déterminer la limite de la suite (\frac{u_n}{v_n}).
Exercice n°12 : ( algorithme, démonstration par récurrence, suite croissante, calcul de limites)
Un biologiste souhaite étudier l’évolution de la population d’une espèce animale dans une réserve.
Cette population est estimée à 12 000 individus en 2016. Les contraintes du milieu naturel font que la population ne peut pas dépasser les 60 000 individus.
Partie A : un premier modèle.
Dans une première approche, le biologiste estime que la population croît de 5 % par an.
L’évolution annuelle de la population est ainsi modélisée par une suite (v_n) où v_n représente le nombre d’individus, exprimé en milliers, en 2016+n. On a donc v_0=12.
1. Déterminer la nature de la suite (v_n) et donner l’expression de v_n en fonction de n.
2. Ce modèle répond-il aux contraintes du milieu naturel ?
Partie B : un second modèle
Le biologiste modélise ensuite l’évolution annuelle de la population par une suite (u_n) définie
par u_0=12 et, pour tout entier naturel n , u_{n+1}=-\frac{1.1}{605}u_n^2+1.1u_n
1. On considère la fonction g définie sur \mathbf{R} par
g(x)=-\frac{1.1}{605}x^2+1.1x
a. Justifier que g est croissante sur [0; 60].
b. Résoudre dans \mathbf{R} l’équation g(x)=x.
2. On remarquera que u_{n+1}=g(u_n).
a. Calculer la valeur arrondie à 10^{-3} de u_1. Interpréter
b. Démontrer par récurrence que, pour tout entier naturel n , 0\leq u_n\leq 55.
c. Démontrer que la suite (u_n) est croissante.
d. En déduire la convergence de la suite (u_n).
e. On admet que la limite l de la suite (u_n) vérifie g(l)=l. En déduire sa valeur et l’interpréter dans le contexte de l’exercice
3. Le biologiste souhaite déterminer le nombre d’années au bout duquel la population dépassera les 50 000 individus avec ce second modèle.
Il utilise l’algorithme suivant.
n un entier naturel
u un nombre réel
n prend la valeur 0
u prend la valeur 12
Tant Que . . . . . . . . . . . . . . . . . . . .
u prend la valeur . . . . . . . . . . . . . .
n prend la valeur . . . . . . . . . . . . . .
Fin Tant Que
Afficher . . . . . . . . . . . . . . . . . . . . .
Recopier et compléter cet algorithme afin qu’il affiche en sortie le plus petit entier k tel que
u_k>50.
Exercice n°13 : ( démonstration par récurrence, suite croissante, calcul de limites, représenter graphiquement des termes de suites)
Soit f la fonction définie sur l’intervalle [0; 4] par f(x)=\frac{2+3x}{4+x}
Partie A
On considère la suite (u_n) définie par : u_0=3 et pour tout entier naturel n , u_{n+1}=f(u_n).
On admet que cette suite est bien définie.
1. Calculer u_1.
2. Montrer que la fonction f est croissante sur l’intervalle [0; 4].
3. Montrer par récurrence que pour tout entier naturel n , 1\leq u_{n+1}\leq u_{n}\leq 3.
4. a. En déduire que la suite (u_n) est convergente.
4. b. On admet que la limite l de (u_n) vérifie l=\frac{2+3l}{4+l}. Calculer l.
Partie B
On considère la suite (v_n) définie par :
v_0=0.1 et pour tout entier naturel n, v_{n+1}=f(v_n).
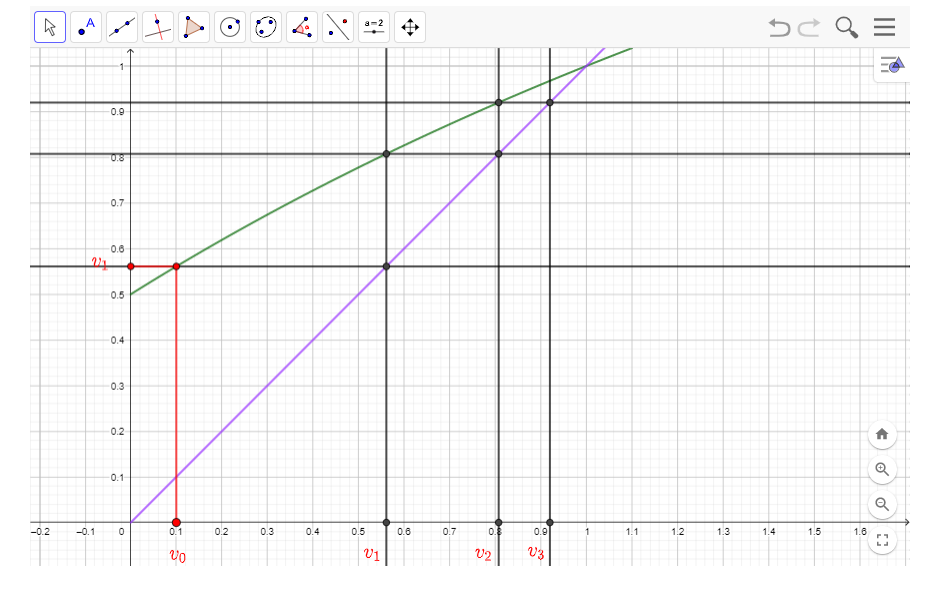
1. Dans la fenêtre active Géogébra ci-dessous on a représenté la courbe représentative de la fonction f en vert et une partie de la droite D d’équation y=x en violet.
Placer sur l’axe des abscisses par construction géométrique les termes v_1, v_2 et v_3.
Quelle conjecture peut-on formuler sur le sens de variation et le comportement de la suite (v_n) quand n tend vers l’infini ?
2. a. Montrer que pour tout entier naturel n , 1-v_{n+1}=\frac{2}{4+v_n}(1-v_n).
b. On admet que pour tout entier naturel n, v_n\geq 0. Montrer alors que 0\leq \frac{1}{4+v_n} \leq \frac{1}{4}.
c. Montrer par récurrence que pour tout entier naturel n , 0\leq 1-v_n\leq (\frac{1}{2})^n.
3. En déduire la limite de la suite (v_n).
Exercice n°14
( démonstration par récurrence, suite croissante, calcul de limites, représenter graphiquement des termes de suites)
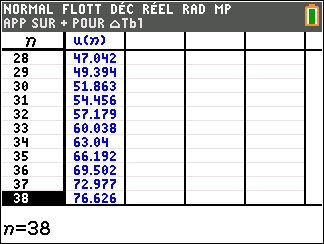
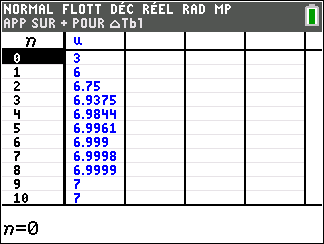
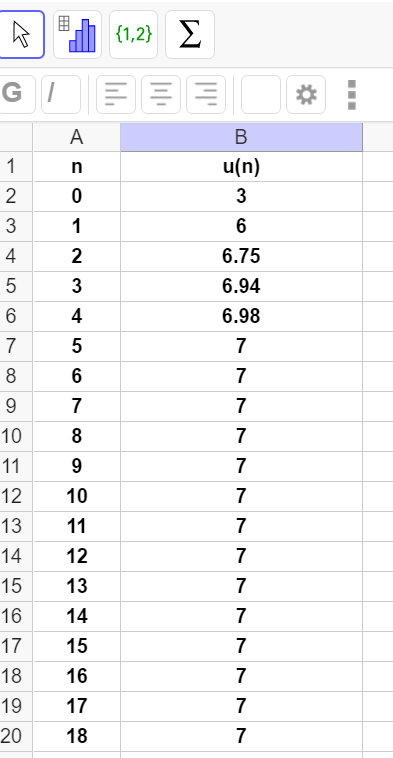
Soit (u_n) la suite définie par u_0=3, u_1=6 et, pour tout entier naturel n:
u_{n+2}=\frac{5}{4}u_{n+1}-\frac{1}{4}u_{n}.
Le but de cet exercice est d’étudier la limite éventuelle de la suite (u_n).
Partie A :
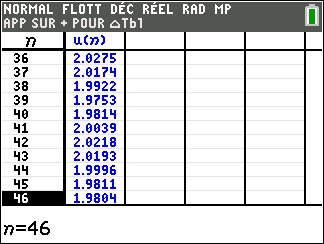
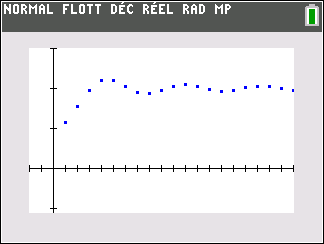
1. On souhaite calculer les valeurs des premiers termes de la suite (u_n). Utiliser le tableur de la fenêtre Géogébra ci-dessous. Pour cela copier la formule adéquate dans la cellule B4 et tirer vers le bas.
2. Que peut-on conjecturer pour la convergence de la suite (u_n) ?
Partie B : Étude de la suite (u_n)
On considère les suites (v_n) et (w_n) définies pour tout entier naturel n par :
v_n=u_{n+1}-\frac{1}{4}u_n et w_n=u_{n}-7.
1. a. Démontrer que (v_n) est une suite constante.
b. En déduire que, pour tout entier naturel n , u_{n+1}=\frac{1}{4}u_n+\frac{21}{4}.
2. a. En utilisant le résultat de la question 1. b. montrer par récurrence que, pour tout
entier naturel n , u_n<u_{n+1}<15.
b. En déduire que la suite (u_n) est convergente
3. a. Démontrer que (w_n) est une suite géométrique dont on précisera le premier terme et la raison.
b. En déduire que, pour tout entier naturel n , u_n=7-(\frac{1}{4})^{n-1}.
c. Calculer la limite de la suite (u_n).