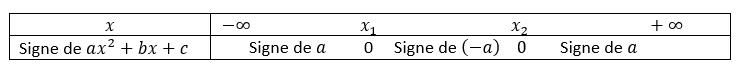Sommaire
Convexité d’une fonction
Définition : sécante
Soient deux points A et B situés sur la courbe représentative d’une fonction f alors la droite (AB) est appelée sécante.
Définitions : convexe et concave
Soit une fonction f et C_f sa courbe représentative dans un repère.
- f est convexe sur un intervalle I si pour tout x\in I , C_f est en-dessous de ses sécantes.
- f est concave sur un intervalle I si pour tout x\in I , C_f est au-dessus de ses sécantes.
Exemple n°1
La fonction carré définie sur \mathbf{R} est convexe. Pour s’en convaincre, on peut déplacer les points A et B sur la courbe et constater que la courbe C_f est en-dessous de ses sécantes.
Pour cela, cliquer sur le premier onglet en haut à gauche ( la flèche) et en sélectionnant Déplacer dans le menu déroulant. Ensuite dans le repère placer la flèche sur un des deux points et le bouger.
Exemple n°2
La fonction cube définie sur \mathbf{R} est convexe sur [0;+\infty[ et concave sur ]-\infty;0]. Pour s’en convaincre, on peut déplacer les points A et B sur la courbe ( à droite de l’axe des ordonnées) et constater que la courbe C_f est en-dessous de ses sécantes et au-dessus de ses sécantes à gauche de l’axe des ordonnées.
Pour cela, cliquer sur le premier onglet en haut à gauche ( la flèche) et en sélectionnant Déplacer dans le menu déroulant. Ensuite dans le repère placer la flèche sur un des deux points et le bouger.
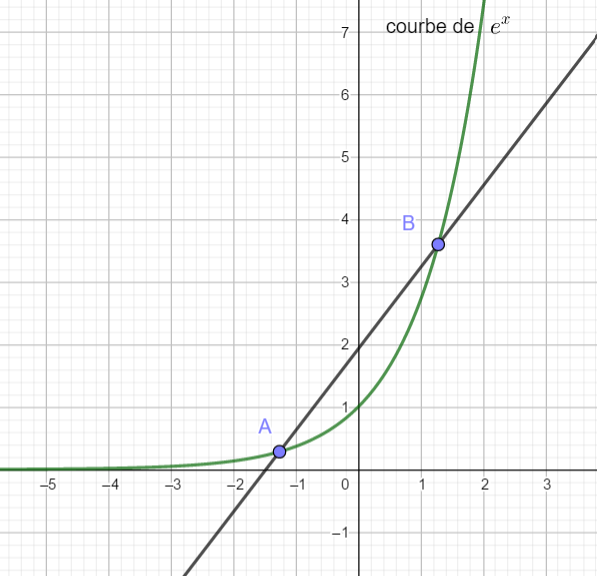
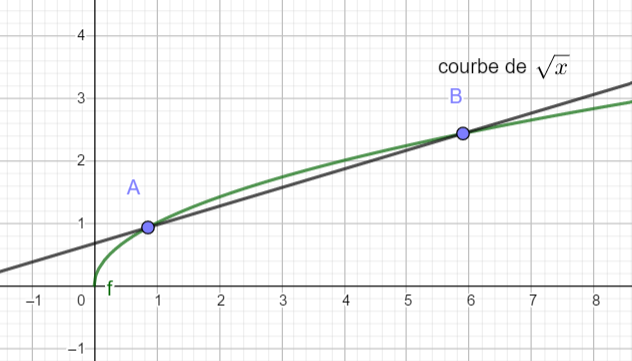
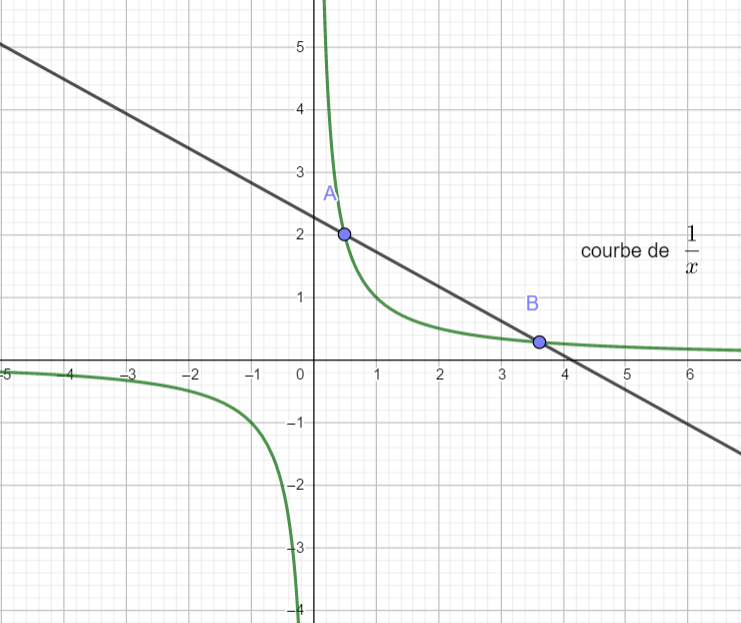
Exercice n°1
A l’aide des trois graphiques ci-dessous déterminer si les fonctions sont concaves ou convexes. Si la concavité change, préciser les intervalles où f est concave et où f est convexe.
Propriétés : inégalités
- Si f est convexe sur un intervalle I si pour tout x\in I , pour tout y\in I et pour tout t\in I [0;1] , on a :
f(tx+(1-t)y)\leq tf(x)+(1-t)f(y).
- Si f est concave sur un intervalle I si pour tout x\in I , pour tout y\in I et pour tout t\in I [0;1] , on a :
f(tx+(1-t)y)\geq tf(x)+(1-t)f(y).
Exercice n°2
En utilisant le fait que la fonction carré est convexe sur \mathbf{R} , démontrer que si a et b sont strictements positifs alors
(a+b)^2\leq 2(a^2+b^2).
Exercice n°3
En utilisant le fait que la fonction racine carrée est concave sur ]0;+\infty[ , démontrer que si a et b sont strictements positifs alors
\sqrt{a+b}\leq \frac{\sqrt{2}}{2}(\sqrt{a}+\sqrt{b}).
Fonction convexe et dérivées première et dérivée seconde
Théorème
Soit une fonction f une fonction deux fois dérivable sur un intervalle I et f’ sa fonction dérivée.
- La fonction f est convexe sur I si et seulement si la fonction f’ est croissante.
- La fonction f est concave sur I si et seulement si la fonction f’ est décroissante.
Définition : dérivée seconde
Soit une fonction f une fonction deux fois dérivable sur un intervalle I et f’ sa fonction dérivée.
On appelle dérivée seconde de la fonction f notée f", la dérivée de la dérivée f’.
Exercice n°4
Calculer la dérivée seconde de la fonction f notée f" dans chaque cas.
f(x)=e^x pour x \in \mathbf{R}
f(x)=\sqrt{x} pour x \in ]0;+\infty[
f(x)=\frac{1}{x} pour x \in ]-\infty;0[\cup ]0;+\infty[
Théorème : convexité et dérivée seconde
Soit une fonction f une fonction deux fois dérivable sur un intervalle I et f" sa fonction dérivée seconde.
- f est convexe si et seulement si pour tout réel x de I, f"(x) est positive.
- f est concave si et seulement si pour tout réel x de I, f"(x) est négative.
Exercice n°5
Retrouver les résultats de l’exercice n°1 en étudiant le signe des dérivées seconde obtenues à l’exercice n°4.
f(x)=e^x pour x \in \mathbf{R}
f(x)=\sqrt{x} pour x \in ]0;+\infty[
f(x)=\frac{1}{x} pour x \in ]-\infty;0[\cup ]0;+\infty[
Utiliser la page Géogébra pour ci-dessous pour vérifier si les calculs de de dérivées sont exacts. Pour cela, saisir, par exemple \frac{2}{x^3}>0 sur la ligne n°1 et cliquer sur le 7ème onglet (X=). Apparait alors à l’écran Résoudre: {x>0}.
Tangente et point d’inflexion
Théorème : dérivée seconde et tangente
Soit une fonction f une fonction deux fois dérivable sur un intervalle I et f" sa fonction dérivée seconde.
si f" est positive sur I alors la courbe de la fonction f est située au-dessus de ses tangentes.
Illustration
On s’intéresse à la fonction exponentielle. On a établi précédemment que sa dérivée seconde vaut e^x et qu’ elle est positive.
Cliquer sur le premier onglet à gauche et sélectionner Déplacer dans le menu déroulant. Puis dans le repère déplacer le point A et s’assurer que la courbe reste au-dessus de ses tangentes.
Remarque
si f" est négative sur I alors la courbe de la fonction f est située en-dessous de ses tangentes.
Illustration
On s’intéresse à la fonction f(x)=\sqrt{x} définie sur [0;+\infty[. On a établi précédemment que sa dérivée seconde est négative.
Cliquer sur le premier onglet à gauche et sélectionner Déplacer dans le menu déroulant. Puis dans le repère déplacer le point A et s’assurer que la courbe reste en-dessous de ses tangentes.
Définition : point d’inflexion
Soit une fonction f une fonction deux fois dérivable sur un intervalle I et C_f sa courbe représentative dans un repère orthonormé.
Soit A un point de C_f et T_A la tangente à la courbe C_f en A.
On dit que A est un point d’inflexion pour C_f si au point A, la courbe C_f traverse la tangente T_A.
Illustration
On s’intéresse à la fonction f(x)=x^3, l’origine du repère est un point d’inflexion.
Cliquer sur le premier onglet à gauche et sélectionner Déplacer dans le menu déroulant. Puis dans le repère déplacer le point A et s’assurer que la courbe traverse la tangente au point d’abscisse 0.
Propriété : point d’inflexion
Pour qu’il y ait point d’inflexion, il faut que f" change de signe, donc que f’ change de variations ou encore que f change de convexité.
Illustration
Reprenons la fonction f(x)=x^3.
f'(x)=3x^2 et f"(x)=6x\\f"(x) change de signe pour x=0
Donc l’origine du repère est bien un point d’inflexion.
Exercice n°6
On considère la fonction f définie et dérivable sur \mathbf{R} par f(x)=xe^{-x}
Cette fonction admet sur R une dérivée f’ et une dérivée seconde f".
- Montrer que f'(x)=(1-x)e^{-x}.
2.a. Montrer que f"(x)=(2+x)e^{-x}.
2.b. Etudier le signe de f"(x) et en déduire les coordonnées d’éventuels points d’inflexion de la courbe C_f
Exercice n°7
On considère la fonction f définie et dérivable sur \mathbf{R} par f(x)=2x^2e^{-x}
Cette fonction admet sur R une dérivée f’ et une dérivée seconde f".
- Montrer que f'(x)=(4x-2x^2)e^{-x}
2.a. Montrer que f"(x)=(2x^2-8x+4)e^{-x}.
2.b. Etudier le signe de f"(x) et en déduire les coordonnées d’éventuels points d’inflexion de la courbe C_f