logo

T. Vecteurs de l’espace.

Sommaire

Translations et vecteurs

Définitions 

M et M’ sont deux points distincts de l’espace.

La translation qui transforme M en M’ est appelée translation de vecteur \overrightarrow{MM’}.

Le vecteur \overrightarrow{MM’} a pour direction celle de la droite (MM’) , a pour sens celui de M vers M’ et a pour norme la longueur MM’.

Exemple n°1

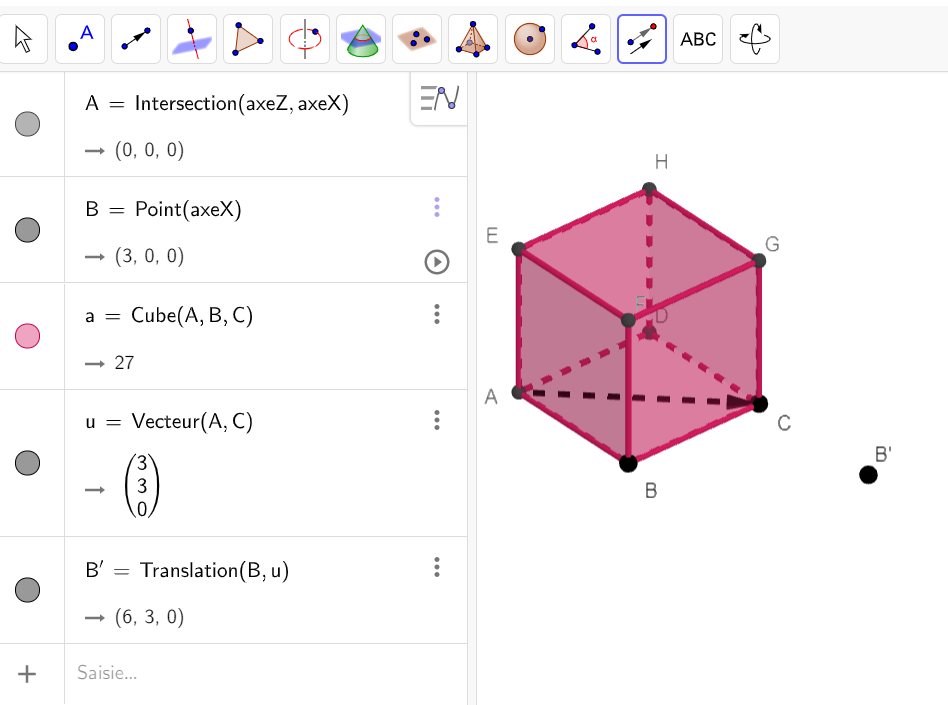
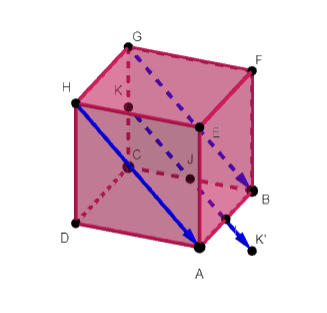
construire l’image du point B par la translation de vecteur \overrightarrow{AC} à l’aide de Géogébra.

1.construire le vecteur \overrightarrow{AC} :

cliquer sur le troisième onglet et sélectionner Vecteur dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point  A ( origine du vecteur \overrightarrow{AC}) et ensuite sur le point  C ( extrémité du vecteur \overrightarrow{AC})

2.Construire B’ l’image de B par la translation de vecteur \overrightarrow{AC} : 

 cliquer sur le douzième onglet et sélectionner Translation dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point  B  et ensuite sur le vecteur \overrightarrow{AC}.

correction

Exercice n°1

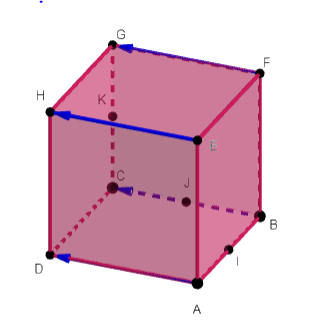
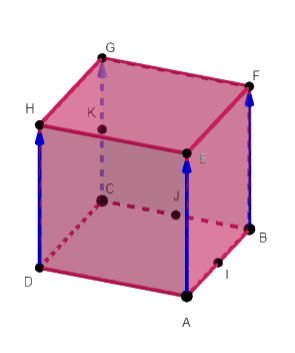
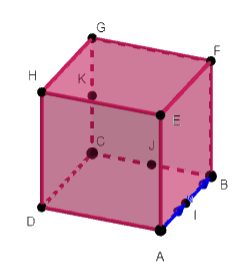
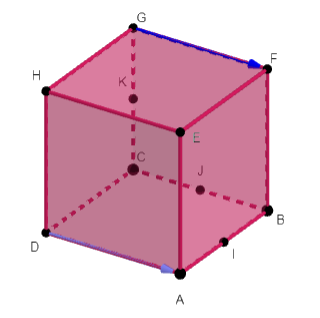
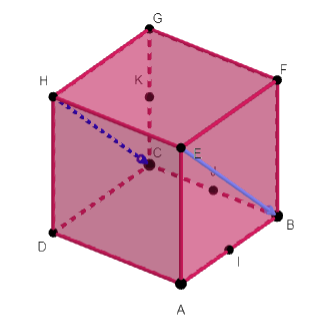
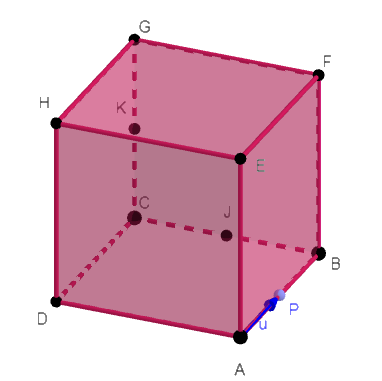
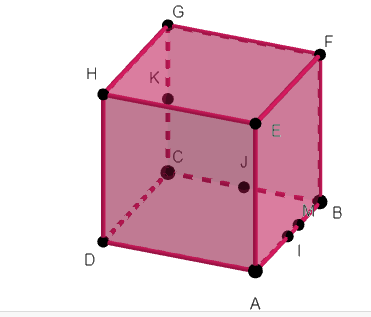
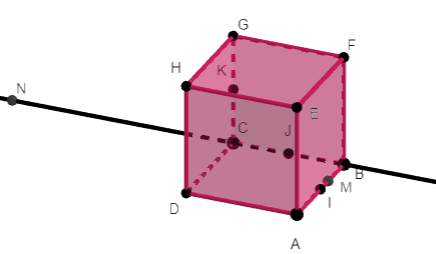
Dans le cube ABCDEFGH, les points I , J et K sont les milieux respectifs de [AB] , [BC] et [CG].

  1. Citez un  vecteur égal à 

a. \overrightarrow{AD}

correction

b. \overrightarrow{AE}

correction

c. \overrightarrow{BD}

correction

d. \overrightarrow{GB}

correction

2. Complétez les pointillés à l’aide d’un point de la figure. 

a. \overrightarrow{AI}=\overrightarrow{I…}

correction

b. \overrightarrow{DC}=\overrightarrow{…G}

correction

c. \overrightarrow{D…}=\overrightarrow{GF}

correction

d. \overrightarrow{HC}=\overrightarrow{E…}

correction

Opérations sur les vecteurs, combinaisons linéaires

Somme de deux vecteurs.

A , B et C sont trois points de l’espace.

Relation du parallélogramme

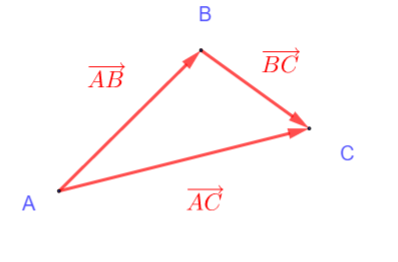
\overrightarrow{AB}+ \overrightarrow{AD}= \overrightarrow{AC} où D est le quatrième sommet du parallélogramme ABCD.

Relation de Chasles 

quelque soient les points A, B, C on a la relation suivante \overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}

Exemple n°2 

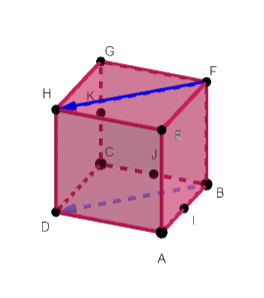
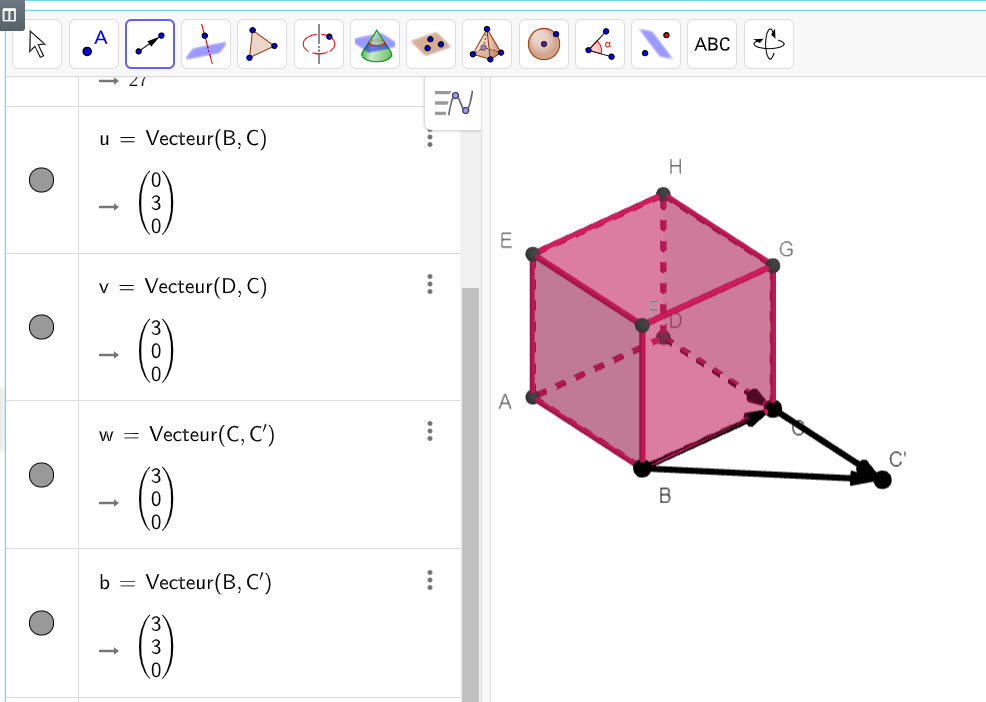
construire la somme  \overrightarrow{BC}+\overrightarrow{DC} à l’aide de Géogébra. Utiliser la fenêtre de l’exercice n°1.

1.construire le vecteur \overrightarrow{BC} (cette partie est en rouge car elle est facultative) :

cliquer sur le troisième onglet et sélectionner Vecteur dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point  B ( origine du vecteur \overrightarrow{BC}) et ensuite sur le point  C ( extrémité du vecteur \overrightarrow{BC})

2.construire le vecteur \overrightarrow{DC} :

cliquer sur le troisième onglet et sélectionner Vecteur dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point  D ( origine du vecteur \overrightarrow{DC}) et ensuite sur le point  C ( extrémité du vecteur \overrightarrow{DC})

3.construire un représentant du deuxième vecteur (ici : le vecteur  \overrightarrow{DC}) à partir de l’extrémité du premier vecteur ( ici : C du vecteur \overrightarrow{BC}) .

Cliquer sur le troisième onglet et sélectionner Représentant dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point C ( extrémité du premier vecteur \overrightarrow{BC}) et ensuite sur le vecteur \overrightarrow{DC} (le deuxième vecteur de la somme  \overrightarrow{BC}+\overrightarrow{DC}). On obtient alors le point C'.

4. tracer le vecteur somme \overrightarrow{BC}+\overrightarrow{DC}:

Cliquer sur le troisième onglet et sélectionner Vecteur dans le menu déroulant. Ensuite, sur la figure, cliquer en premier sur le point  B ( origine du premier vecteur \overrightarrow{BC}) et ensuite sur le point  C' (extrémité du représentant du 2nd vecteur \overrightarrow{DC})

correction

Exercice n°2

On considère le cube ABCDEFGH de l’exemple n°1.

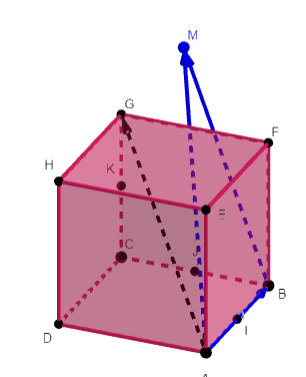
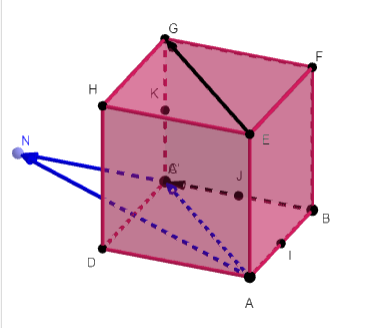
Construire les points les points M , N et P définis par 

a. \overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AG}

correction

b. \overrightarrow{AN}=\overrightarrow{EG}+\overrightarrow{BC}

correction

Produit d’un vecteur par un nombre réel.

A et B sont deux points de l’espace. \lambda est un nombre réel.

1er cas : si \lambda est positif

\lambda\overrightarrow{AB} a pour direction: la direction du vecteur \overrightarrow{AB}\\ \lambda\overrightarrow{AB} a pour sens: le sens du vecteur \overrightarrow{AB}(de A vers B)

\lambda\overrightarrow{AB} a pour norme: la norme du vecteur \overrightarrow{AB} mutipliée par \lambda

2nd cas : si \lambda est négatif

\lambda\overrightarrow{AB} a pour direction: la direction du vecteur \overrightarrow{AB}\\ \lambda\overrightarrow{AB} a pour sens: le sens contraire de  \overrightarrow{AB}(de B vers A)

\lambda\overrightarrow{AB} a pour norme: la norme du vecteur \overrightarrow{AB} mutipliée par -\lambda

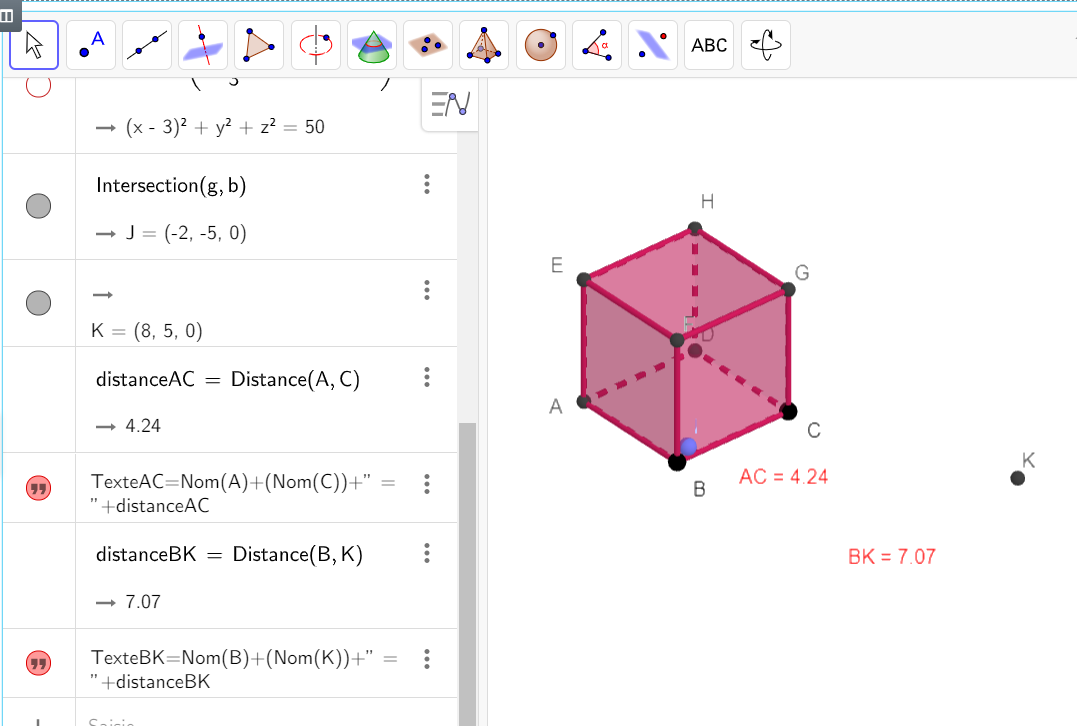
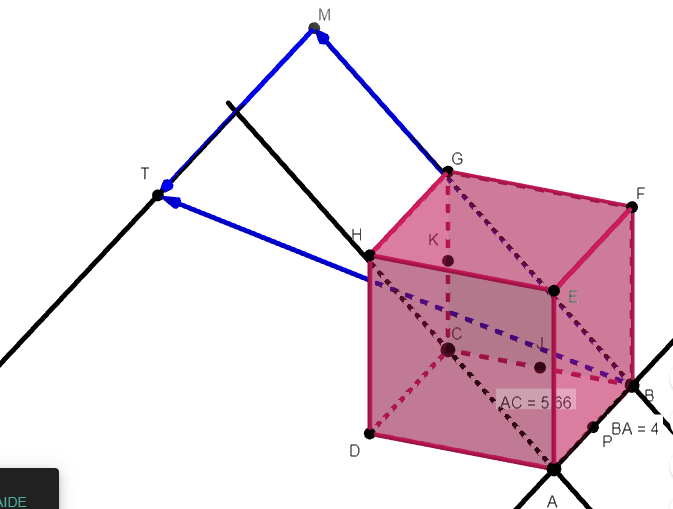
Exemple n°3 : Placer B’ tel que \overrightarrow{BB’ }=\frac{5}{3} \overrightarrow{AC } avec Géogébra. Utiliser la fenêtre au-dessus.

Les vecteurs \overrightarrow{BB’ } et \frac{5}{3} \overrightarrow{AC } ont même direction. Il faut tracer une droite parallèle à (AC) passant par  B.

Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Droite dans le menu déroulant. Puis, sur la figure, cliquer sur le point A et sur le point C.

Cliquer sur le quatrième onglet à partir de la gauche en haut et sélectionner Parallèle dans le menu déroulant. Puis, sur la figure,  cliquer sur la droite (AC) qu’on vient de tracer et sur le point B.

La longueur ( ou norme) du vecteur \overrightarrow{BB’ } est \frac{5}{3} fois  \overrightarrow{AB } . Avec Géogébra, tracer la sphère de centre B et de rayon \frac{5}{3}AC.

Cliquer sur le dixième onglet à partir de la gauche en haut et sélectionner Sphère (centre-rayon) dans le menu déroulant. Puis, sur la figure, cliquer sur le point B et dans la case Rayon écrire 5/3*AC.

Remarque : la sphère et la droite ont deux points communs.

Les vecteurs \overrightarrow{BB’ } et \frac{5}{3} \overrightarrow{AC } ont même sens car le vecteur      \overrightarrow{AB } est multiplié par \frac{5}{3} qui est un nombre positif. Donc parmi les deux points d’intersection obtenus précédemment , on ne garde que celui où on va de B vers B’ comme on va de A vers C.

On l’appelle C’.

Cliquer gauche sur le point d’intersection que l’on a choisi et sélectionner Renommer dans le menu déroulant. Appeler le point C’.

correction

Propriétés 

\overrightarrow{u} et \overrightarrow{v} sont deux vecteurs de l’espace. \lambda et \lambda’ sont deux nombres réels.

\lambda\overrightarrow{u}=0\iff \lambda=0   ou  \overrightarrow{u}=\overrightarrow{0} .

(-1)\overrightarrow{u}=- \overrightarrow{u} et \overrightarrow{u}+ (-\overrightarrow{v})=\overrightarrow{u}-\overrightarrow{v} \\ \lambda(\overrightarrow{u}+ \overrightarrow{v})=\lambda\overrightarrow{u}+\lambda\overrightarrow{v} \\(\lambda+\lambda’)\overrightarrow{u}=\lambda\overrightarrow{u}+\lambda’\overrightarrow{u} \\\lambda(\lambda’\overrightarrow{u})=(\lambda\lambda’)\overrightarrow{u}

Exercice n°3

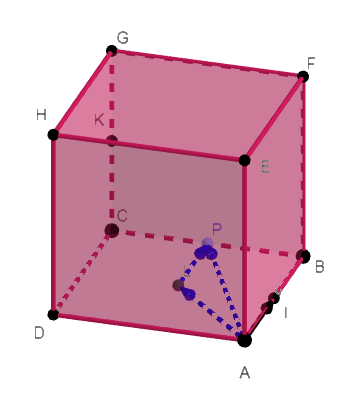
On considère le cube ABCDEFGH de l’exemple n°1.

Construire le point  P défini par \overrightarrow{AP}+\overrightarrow{BP}=\overrightarrow{AC}

correction

Exercice n°4

On considère le cube ABCDEFGH de l’exemple n°1.

  1. Construire les points les points P  et T définis par

a. \overrightarrow{AP}=\frac{1}{2}\overrightarrow{AB}

correction

b. \overrightarrow{BT}=3\overrightarrow{AC}-2\overrightarrow{AB}

correction

2. Montrer que les points les points C , P  et T sont alignés.

correction

Exercice n°5

On considère le cube ABCDEFGH de l’exemple n°1.

  1. Construire les points les points M  et N définis par

a. \overrightarrow{BM}=\frac{1}{3}\overrightarrow{BA}

correction

b. \overrightarrow{CN}=2\overrightarrow{BC}

correction

2. Montrer que les points les vecteurs  \overrightarrow{MC} et \overrightarrow{AN} sont colinéaires.

correction

Définition

Dire qu’un vecteur \overrightarrow{u} est combinaison linéaire des vecteurs \overrightarrow{v}  , \overrightarrow{w} et \overrightarrow{t} signifie qu’il existe des réels x, y, z tels que  

\overrightarrow{u}=x\overrightarrow{v}+y\overrightarrow{w}+z\overrightarrow{t}

©2020 – Math’O karé SAS

Réponses possibles :

\overrightarrow{AD}, \overrightarrow{EH}, \overrightarrow{FG} ou \overrightarrow{BC}.

Et aussi  2\overrightarrow{BJ} et 2\overrightarrow{JC}

 

Réponses possibles :

\overrightarrow{AE}, \overrightarrow{DH}, \overrightarrow{CG} ou \overrightarrow{BF}.

Et aussi  2\overrightarrow{CK} et 2\overrightarrow{KG}

Réponses possibles :

\overrightarrow{BD}, \overrightarrow{FH}.

Réponses possibles :

\overrightarrow{GB}, \overrightarrow{HA}.

Et aussi 2\overrightarrow{KJ}

Réponse:

\overrightarrow{AI}=\overrightarrow{IB}.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Réponse:

\overrightarrow{DA}=\overrightarrow{GF}.

Réponse:

\overrightarrow{HC}=\overrightarrow{EB}.

Pour construire M tel que \overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AG}  :

A partir du point A, je reporte le vecteur \overrightarrow{AB}. A partir de l’extrémité du vecteur \overrightarrow{AB} ( c’est-à-dire B) je reporte un vecteur égal au vecteur \overrightarrow{AG} ( on dit aussi représentant du vecteur \overrightarrow{AG}).

Pour construire le vecteur somme \overrightarrow{AB}+\overrightarrow{AG} je trace le vecteur qui a A pour  origine et pour extrémité : l’extrémité du représentant c’est-à-dire M.

Pour construire N tel que \overrightarrow{AN}=\overrightarrow{EG}+\overrightarrow{BC}  :

A partir du point A, je reporte un vecteur égal au vecteur \overrightarrow{EG} ( on dit aussi représentant du vecteur \overrightarrow{EG}). A partir de l’extrémité du représentant de  \overrightarrow{EG}, je reporte un vecteur égal au vecteur \overrightarrow{BC} ( on dit aussi représentant du vecteur \overrightarrow{BC}).

Pour construire le vecteur somme \overrightarrow{EG}+\overrightarrow{BC} je trace le vecteur qui a A pour  origine et pour extrémité : l’extrémité du représentant de \overrightarrow{BC} c’est-à-dire N.

Afin de vérifier, on peut mesurer AC et BK et vérifier que \frac{BK}{AC}=\frac{5}{3} .

On peut aussi rendre des objets invisibles sans les effacer. Pour cela cliquer droit sur l’objet à faire disparaître et décocher la case Afficher l’objet.

Il n’est pas possible de construire directement  P tel que \overrightarrow{AP}+\overrightarrow{BP}=\overrightarrow{AC} car dans cette égalité vectorielle le point P apparaît dans deux vecteurs \overrightarrow{AP} et \overrightarrow{BP}.

On choisit de garder le vecteur \overrightarrow{AP} et de transformer  \overrightarrow{BP} en \overrightarrow{BA}+\overrightarrow{AP} à l’aide de la relation de Chasles.

On remplace \overrightarrow{BP} par  \overrightarrow{BA}+\overrightarrow{AP} dans \overrightarrow{AP}+\overrightarrow{BP}=\overrightarrow{AC}

\overrightarrow{AP}+\overrightarrow{BA}+\overrightarrow{AP}=\overrightarrow{AC}

On réduit

2\overrightarrow{AP}+\overrightarrow{BA}=\overrightarrow{AC}

On enlève \overrightarrow{BA} de chaque côté.

2\overrightarrow{AP}=\overrightarrow{AC}-\overrightarrow{BA}

On divise par 2 de chaque côté.

\overrightarrow{AP}=\frac{1}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{BA}

On remplace -\frac{1}{2}\overrightarrow{BA} par \frac{1}{2}\overrightarrow{AB}

\overrightarrow{AP}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}

 

Pour construire P tel que \overrightarrow{AP}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}  :

A partir du point A, je reporte le vecteur \frac{1}{2}\overrightarrow{AC} . A partir de l’extrémité du vecteur \frac{1}{2}\overrightarrow{AC} , je reporte un vecteur égal au vecteur \frac{1}{2}\overrightarrow{AB} ( on dit aussi représentant du vecteur \frac{1}{2}\overrightarrow{AB} ).

Pour construire le vecteur somme \frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB} je trace le vecteur qui a A pour  origine et pour extrémité : l’extrémité du représentant de \frac{1}{2}\overrightarrow{AB} c’est-à-dire P.

Pour construire P tel que \overrightarrow{AP}=\frac{1}{2}\overrightarrow{AB}  :

A partir du point A, je reporte le vecteur \frac{1}{2}\overrightarrow{AB} et j’obtiens le point P .

 

 

Pour construire T tel que \overrightarrow{BT}=3\overrightarrow{AC}-2\overrightarrow{AB} ce qui revient à  construire T tel que \overrightarrow{BT}=3\overrightarrow{AC}+2\overrightarrow{BA}

A partir du point B, je reporte un vecteur égal au vecteur 3\overrightarrow{AC}. A partir de l’extrémité du 3\overrightarrow{AC}, je reporte un vecteur égal au vecteur 2\overrightarrow{BA} ( on dit aussi représentant du vecteur 2\overrightarrow{BA}).

Pour construire le vecteur somme 3\overrightarrow{AC}+2\overrightarrow{BA} je trace le vecteur qui a B pour  origine et pour extrémité : l’extrémité du représentant de 2\overrightarrow{BA} c’est-à-dire T.

On va distinguer deux types de points : ceux du départ, les points initiaux  A,B,C et les points nouvellement construits : P,T.

Pour montrer que les points C,P,T sont alignés, on peut montrer que 

\overrightarrow{CP} et \overrightarrow{CT} sont colinéaires

\overrightarrow{PC} et \overrightarrow{PT} sont colinéaires

\overrightarrow{TC} et \overrightarrow{TP} sont colinéaires

Remarque : comme on a trois points et deux vecteurs, il faudra forcément utiliser un point deux fois. Le mieux est de choisir un point initial ( ici C )

Nous allons montrer que \overrightarrow{CP} et \overrightarrow{CT} sont colinéaires.

Pour cela, on présente la démonstration sous forme de deux colonnes:

On veut exprimer le vecteur   \overrightarrow{CP} en fonction de vecteurs ne comportant que des points initiaux.

Il faut faire disparaître le point nouvellement construit P. Comme il apparaît dans l’énoncé dans l’égalité suivante :  \overrightarrow{AP}=\frac{1}{2}\overrightarrow{AB} , on va utiliser la relation de Chasles avec le point A.

\overrightarrow{CP}=\overrightarrow{CA}+\overrightarrow{AP}

De cette façon, on peut remplacer   \overrightarrow{AP} par   \frac{1}{2}\overrightarrow{AB}

  \overrightarrow{CP}=\overrightarrow{CA}+\frac{1}{2}\overrightarrow{AB} il n’y a que des points initiaux, on s’arrête.

On veut exprimer le vecteur   \overrightarrow{CT} en fonction de vecteurs ne comportant que des points initiaux.

Il faut faire disparaître le point nouvellement construit T. Comme il apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{BT}=3\overrightarrow{AC}-2\overrightarrow{AB} , on va utiliser la relation de Chasles avec le point B.

\overrightarrow{CT}=\overrightarrow{CB}+\overrightarrow{BT}

De cette façon, on peut remplacer   \overrightarrow{BT} par   3\overrightarrow{AC}-2\overrightarrow{AB}

\overrightarrow{CT}=\overrightarrow{CB}+3\overrightarrow{AC}-2\overrightarrow{AB}

On regarde dans la colonne de gauche et on voit qu’à droite du signe égal sur la dernière ligne se trouvent les vecteurs \overrightarrow{CA} et \overrightarrow{AB}. On les fait donc apparaître avec la relation de Chasles.

\overrightarrow{CT}=\overrightarrow{CA}+\overrightarrow{AB}+3\overrightarrow{AC}-2\overrightarrow{AB}\\ \overrightarrow{CT}=\overrightarrow{CA}+\overrightarrow{AB}-3\overrightarrow{CA}-2\overrightarrow{AB}\\ \overrightarrow{CT}=-2\overrightarrow{CA}-\overrightarrow{AB}

On constate qu’en multipliant par -2, l’égalité vectorielle obtenue dans la colonne de gauche, on aura -2\overrightarrow{CP}=-2\overrightarrow{CA}-\overrightarrow{AB}

Donc : -2\overrightarrow{CP}=\overrightarrow{CT}

Donc les points C,P,T sont alignés

 

 

Pour placer M défini par \overrightarrow{BM}=\frac{1}{3}\overrightarrow{BA} :

A partir du point B , on construit la sphère de centre B et de rayon AB/3 .

On construit ensuite le point d’intersection du segment [AB] avec la sphère et on obtient M .

Pour placer N défini par \overrightarrow{CN}=2\overrightarrow{BC} :

A partir du point C , on construit la sphère de centre C et de rayon 2BC.

On trace la droite (BC).

On construit ensuite l’intersection la droite (BC) avec la sphère et on obtient N ( le point situé sur la demi-droite [BC)).

Nous allons montrer que \overrightarrow{MC} et \overrightarrow{AN} sont colinéaires.

Pour cela, on présente la démonstration sous forme de deux colonnes:

On veut exprimer le vecteur   \overrightarrow{MC} en fonction de vecteurs ne comportant que des points initiaux.

Il faut faire disparaître le point nouvellement construit M . Comme M apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{BM}=\frac{1}{3}\overrightarrow{BA}  on va utiliser la relation de Chasles avec le point B.

\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{BC}

De cette façon, on peut remplacer   \overrightarrow{MB} par   \frac{1}{3}\overrightarrow{AB} 

\overrightarrow{MC}=\frac{1}{3}\overrightarrow{AB}+\overrightarrow{BC}\\ \overrightarrow{MC}=\frac{1}{3}\overrightarrow{AB}+\overrightarrow{BC}

il n’y a que des points initiaux, on s’arrête.

On veut exprimer le vecteur   \overrightarrow{AN} en fonction de vecteurs ne comportant que des points initiaux.

Il faut faire disparaître le point nouvellement construit N. Comme il apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{CN}=2\overrightarrow{BC} , on va utiliser la relation de Chasles avec le point C.

\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}

De cette façon, on peut remplacer   \overrightarrow{CN} par   2\overrightarrow{BC}

\overrightarrow{AN}=\overrightarrow{AC}+2\overrightarrow{BC}

On regarde dans la colonne de gauche et on voit qu’à droite du signe égal sur la dernière ligne se trouvent les vecteurs \overrightarrow{AB} et \overrightarrow{BC}. On les fait donc apparaître avec la relation de Chasles.

\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BC}+2\overrightarrow{BC}\\ \overrightarrow{AN}=\overrightarrow{AB}+3\overrightarrow{BC}

On constate qu’en multipliant par 3, l’égalité vectorielle obtenue dans la colonne de gauche, on aura 3\overrightarrow{MC}=\overrightarrow{AB}+3\overrightarrow{BC}

Donc : 3\overrightarrow{MC}=\overrightarrow{AN}

Donc les vecteurs \overrightarrow{MC} et \overrightarrow{AN} sont colinéaires.

 

 

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.