logo

T. Droites de l’espace

Sommaire

Vecteurs directeurs d’une droite, vecteurs colinéaires.

Définition 

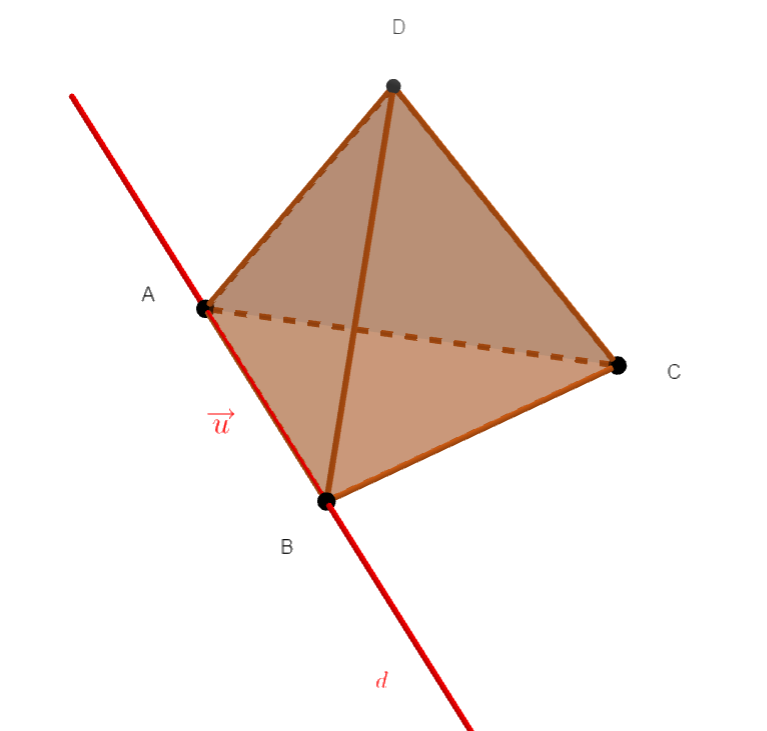
Dire qu’un vecteur non nul \overrightarrow{u} est un vecteur directeur d’une droite d signifie qu’il existe deux points distincts A et B de la droite d tels que \overrightarrow{u}=\overrightarrow{AB}.

Définitions 

Dire que deux vecteurs non nuls \overrightarrow{u} et \overrightarrow{v} sont colinéaires signifie qu’il existe un réel \lambda tel que  \overrightarrow{v}=\lambda\overrightarrow{u}.

Le vecteur nul est colinéaire à tout vecteur.

Positions relatives de deux droites dans l’espace

d et d’ sont deux droites de l’espace de vecteurs directeurs respectifs  \overrightarrow{u} et \overrightarrow{u’}.

\overrightarrow{u} et \overrightarrow{u’} sont colinéaires.

\overrightarrow{u} et \overrightarrow{u’} ne sont pas colinéaires.

d et d’ sont coplanaires et strictement parallèles.

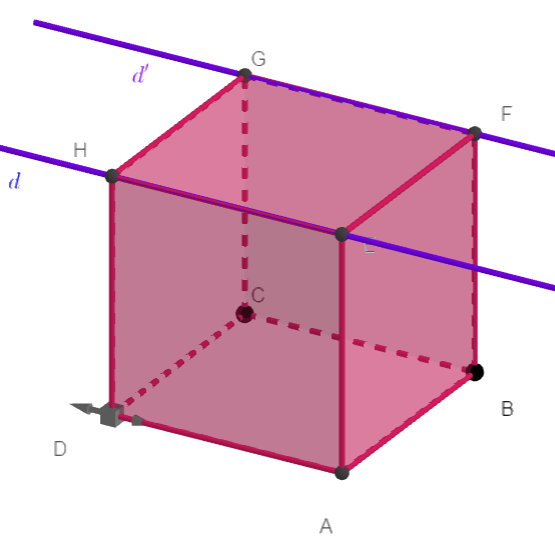
d et d’ sont coplanaires et confondues.

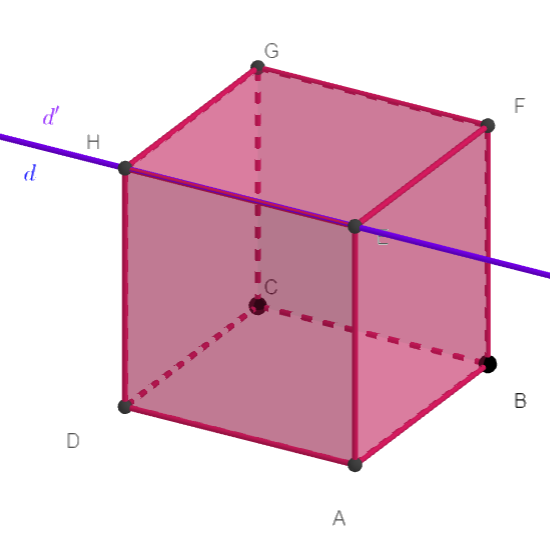
d et d’ sont coplanaires et sécantes.

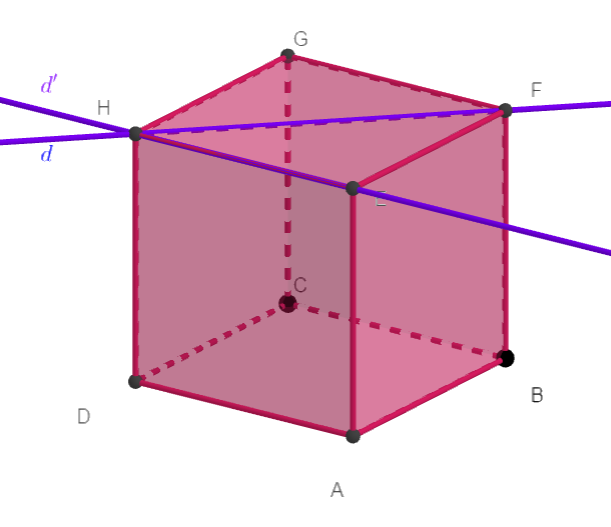
d et d’ sont non coplanaires.

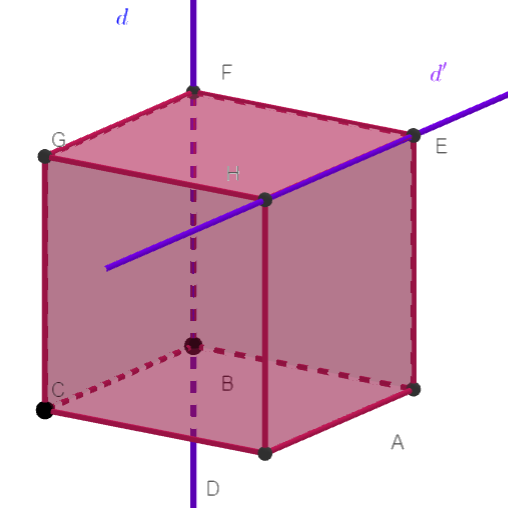
Exercice n°1 

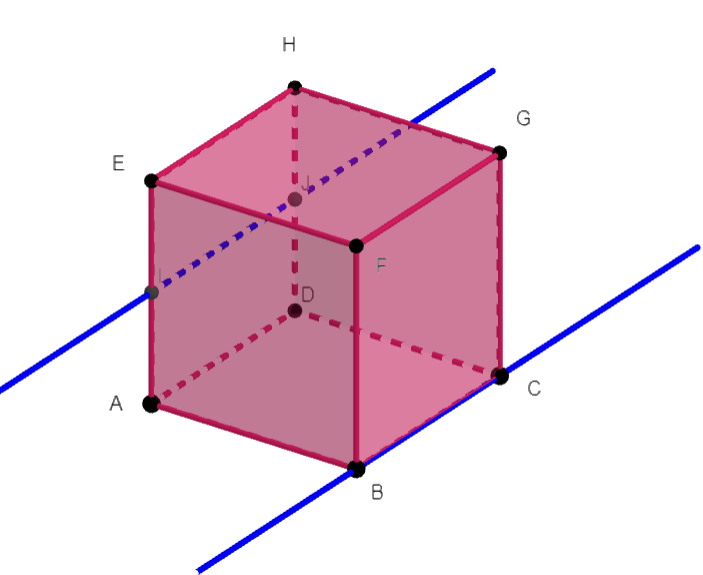
On considère un cube ABCDEFGH.

I et J sont les milieux respectifs de [AE] et [HD].

Etudier la position relative des couples de droites suivants.

Pour tracer, par exemple, la droite  (IJ) avec la fenêtre active Géogébra ci-dessus, cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner droite dans le menu déroulant. Ensuite dans le repère, cliquer sur les points I et J.

Pour déplacer la figure si c’est nécessaire, cliquer sur le dernier onglet en haut à partir de la gauche et sélectionner Déplacer graphique dans le menu déroulant.

a. (IJ) et (BC)

correction

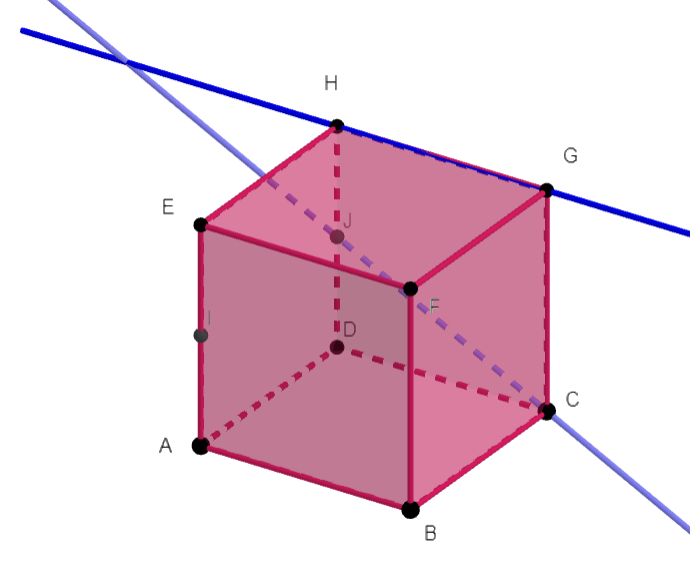
b. (HG) et (JC)

correction

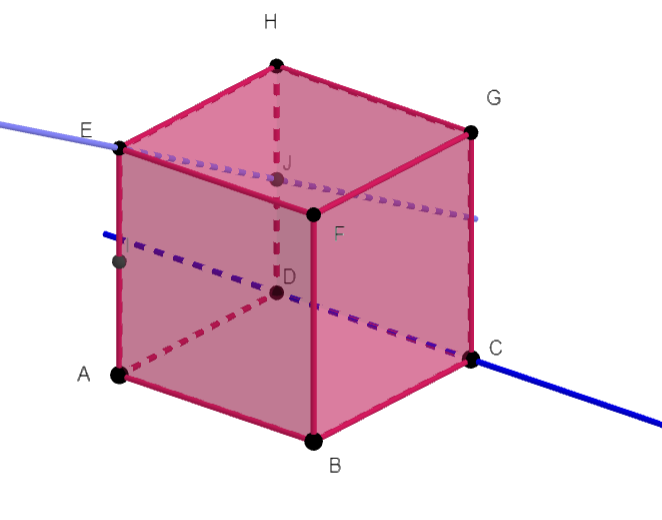
c. (EJ) et (DC)

correction

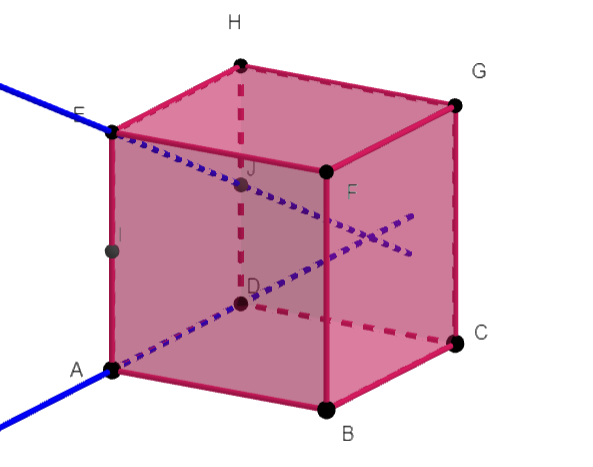
d. (EJ) et (AD)

correction

Caractérisation d’une droite par un point et un vecteur directeur

Propriété

d est la droite de l’espace passant par A et de vecteur directeur \overrightarrow{u}.

Un point M appartient à la droite d si, et seulement si, les vecteurs \overrightarrow{AM} et \overrightarrow{u} sont colinéaires, c’est-à-dire s’il existe un réel \lambda tel que \overrightarrow{AM} =\lambda\overrightarrow{u}

Alignement et parallélisme

Propriétés

Trois points A, B, C de l’espace sont alignés si, et seulement si, les vecteurs \overrightarrow{AB} et \overrightarrow{AC} sont colinéaires.

Les droites  (AB) et (CD)  de l’espace sont parallèles si, et seulement si, les vecteurs \overrightarrow{AB} et \overrightarrow{CD} sont colinéaires.

Exercice n°2

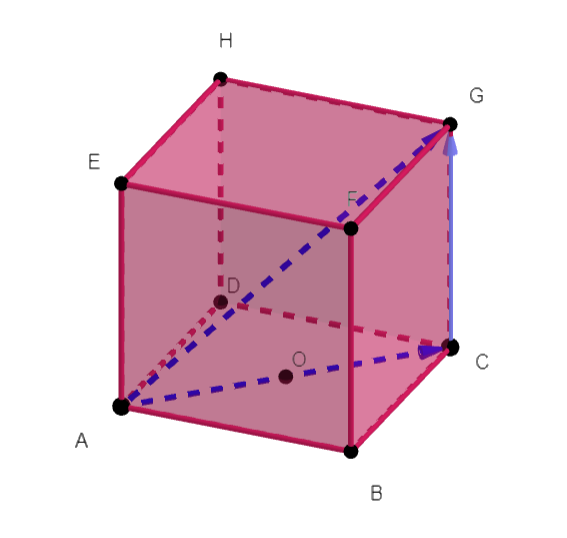
On considère un cube ABCDEFGH. Le point O est le centre de la face ABCD.

M est défini par  \overrightarrow{OM}=\frac{1}{3}\overrightarrow{OE}.

1. Montrer que  \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}.

correction

2. Montrer que  \overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}.

correction

3. Que peut-on en conclure ?

correction

Exercice n°3

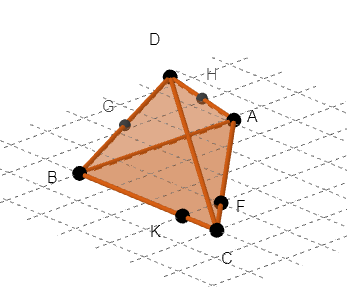
On considère le tétraèdre  ABCD ci-contre.

Le point G est le milieu de  BD et le point H est le milieu de  AD.

K est défini par  \overrightarrow{BK}=\frac{3}{4}\overrightarrow{BC}\\F est défini par  \overrightarrow{AF}=\frac{3}{4}\overrightarrow{AC}.

  1. Montrer que \overrightarrow{GH}=\frac{1}{2}\overrightarrow{BA}
correction

2. Montrer que \overrightarrow{KF}=\frac{1}{4}\overrightarrow{BA}

correction

3. En déduire que \overrightarrow{GH} et  \overrightarrow{KF} sont colinéaires. Que peut-on en déduire pour les droites (GH) et (KF) ?

correction

©2020 – Math’O karé SAS

Réponse:

(IJ) et (BC) sont parallèles.

Réponse:

(HG) et (JC) sont coplanaires et sécantes.

Réponse:

(EJ) et (DC) sont non coplanaires.

Réponse:

(EJ) et (AD) sont sécantes.

On veut exprimer le vecteur   \overrightarrow{AM} en fonction de vecteurs ne comportant que des points initiaux ou points de départ.

Il faut faire disparaître le point nouvellement construit M . Comme M apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{OM}=\frac{1}{3}\overrightarrow{OE}  on va utiliser la relation de Chasles avec le point O.

\overrightarrow{AM}=\overrightarrow{AO}+\overrightarrow{OM}

De cette façon, on peut remplacer   \overrightarrow{OM} par   \frac{1}{3}\overrightarrow{OE} 

\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}\overrightarrow{OE}

Dans l’égalité vectorielle qu’on veut démontrer :   \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}, à droite du signe égal il y a les vecteurs \overrightarrow{AO} et \overrightarrow{AE}. On va donc remplacer \overrightarrow{OE} par \overrightarrow{OA}+\overrightarrow{AE} à l’aide de la relation de Chasles.

\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{AE})

On développe.

\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{AE}

Pour réduire on met au même dénominateur

\overrightarrow{AM}=\frac{3}{3}\overrightarrow{AO}-\frac{1}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}\\ \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}

 

 

On utilise la relation de Chasles :

\overrightarrow{AG}=\overrightarrow{AC}+\overrightarrow{CG}.

Comme O est le milieu de la diagonale [AC] ,  \overrightarrow{AC}=2\overrightarrow{AO} 

\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{CG}

De plus \overrightarrow{CG}=\overrightarrow{AE}, donc

\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}

 

 

On a montré à la question 1 :

\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}

On a montré à la question 2 :

\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}

Si on mutiplie l’égalité vectorielle   \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE} par  3, on obtient :

3\overrightarrow{AM}=2\overrightarrow{AO}+\overrightarrow{AE}

3\overrightarrow{AM} et \overrightarrow{AG} sont égaux au même troisième vecteur 2\overrightarrow{AO}+\overrightarrow{AE} donc:

3\overrightarrow{AM}=\overrightarrow{AG}

Donc les vecteurs \overrightarrow{AM} et \overrightarrow{AG} sont colinéaires.

Donc les points A,M et G sont alignés.

 

Dans le triangle ABD ,  G est le milieu de [DB] et H est le milieu de [DA], d’après le théorème des milieux :

\overrightarrow{GH}=\frac{1}{2}\overrightarrow{BA}.

On veut exprimer le vecteur   \overrightarrow{KF} en fonction d’un vecteur ne comportant que des points initiaux. Il faut faire disparaître les points nouvellement construits K et F . Comme K apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{BK}=\frac{3}{4}\overrightarrow{BC}  et comme F apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{AF}=\frac{3}{4}\overrightarrow{AC} on va utiliser la relation de Chasles avec les points B et A.

\overrightarrow{KF}=\overrightarrow{KB}+\overrightarrow{BA}+\overrightarrow{AF}

De cette façon, on peut remplacer   \overrightarrow{KB} par   \frac{3}{4}\overrightarrow{CB} et   \overrightarrow{AF} par   \frac{3}{4}\overrightarrow{AC}

\overrightarrow{KF}=\frac{3}{4}\overrightarrow{CB}+\overrightarrow{BA}+\frac{3}{4}\overrightarrow{AC}

On continue pour arriver à   \frac{1}{4}\overrightarrow{BA}. On commence par mettre  \frac{3}{4} en facteur dans   \frac{3}{4}\overrightarrow{CB}+\frac{3}{4}\overrightarrow{AC}

\overrightarrow{KF}=\frac{3}{4}(\overrightarrow{CB}+\overrightarrow{AC})+\overrightarrow{BA}

On écrit la somme dans l’ordre pour ne pas se tromper en appliquant la relation de Chasles.

\overrightarrow{KF}=\frac{3}{4}(\overrightarrow{AC}+\overrightarrow{CB})+\overrightarrow{BA}

On applique la relation de Chasles.

\overrightarrow{KF}=\frac{3}{4}\overrightarrow{AB}+\overrightarrow{BA}\\ \overrightarrow{KF}=-\frac{3}{4}\overrightarrow{BA}+\overrightarrow{BA}\\ \overrightarrow{KF}=-\frac{3}{4}\overrightarrow{BA}+\frac{4}{4}\overrightarrow{BA}\\ \overrightarrow{KF}=\frac{1}{4}\overrightarrow{BA}

 

 

On a montré à la question 1 :

\overrightarrow{GH}=\frac{1}{2}\overrightarrow{BA}

On a montré à la question 2 :

\overrightarrow{KF}=\frac{1}{4}\overrightarrow{BA}

Si on mutiplie l’égalité vectorielle   \overrightarrow{GH}=\frac{1}{2}\overrightarrow{BA} par   \frac{1}{2}, on obtient :

\frac{1}{2}\overrightarrow{GH}=\frac{1}{4}\overrightarrow{BA}

\frac{1}{2}\overrightarrow{GH} et \overrightarrow{KF} sont égaux au même troisième vecteur \frac{1}{4}\overrightarrow{BA} donc:

\frac{1}{2}\overrightarrow{GH}=\overrightarrow{KF}

Donc les vecteurs \overrightarrow{GH} et \overrightarrow{KF} sont colinéaires.

Donc les droites (GH) et (KF) sont parallèles.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.