Sommaire
Caractérisation d’un plan de l’espace par un point et une direction
Vocabulaire
Pour définir un plan, il faut un point et deux vecteurs non colinéaires.
On note (A;\overrightarrow{u};\overrightarrow{v}) le plan contenant le point A et dont le couple (\overrightarrow{u},\overrightarrow{v}) est un couple de vecteurs non colinéaires
Propriété
P est le plan (A;\overrightarrow{u};\overrightarrow{v}).
Un point M appartient au plan P si, et seulement si, il existe des réels x et y tels que \overrightarrow{AM}=x\overrightarrow{u}+y\overrightarrow{v}.
Vecteurs coplanaires
Propriété
Dire que \overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} sont coplanaires signifie que pour un point O quelconque de l’espace les points O, A, B, C où \overrightarrow{OA}=\overrightarrow{u} , \overrightarrow{OB}=\overrightarrow{v} et \overrightarrow{OC}=\overrightarrow{w} appartiennent à un même plan.
Un point M appartient au plan P si, et seulement si, il existe des réels x et y tels que \overrightarrow{AM}=x\overrightarrow{u}+y\overrightarrow{v}.
Propriété
\overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} sont des vecteurs de l’espace tels que \overrightarrow{u} et \overrightarrow{v} ne soient pas colinéaires.
\overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} sont coplanaires si, et seulement si, il existe des réels x et y tels que \overrightarrow{w}=x\overrightarrow{u}+y\overrightarrow{v}.
Exercice n°1
ABCD est un tétraèdre.
Les points I , J , K et L sont les milieux respectifs des arêtes [AB] , [AC] , [AD] et [CD] .
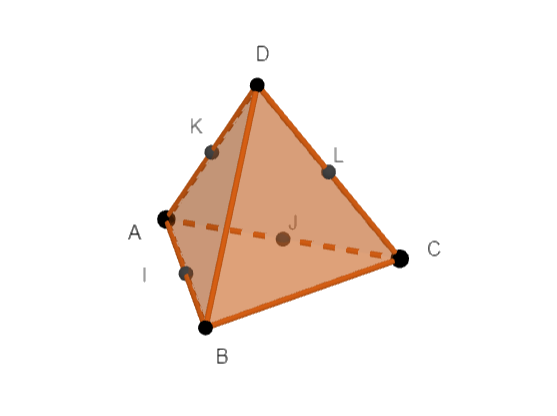
1.a. Justifier que \overrightarrow{IA}=-\frac{1}{2}\overrightarrow{AB} et que \overrightarrow{AJ}=\frac{1}{2}\overrightarrow{AC}
1.b. En déduire que \overrightarrow{IJ}=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}.
2. Justifier que \overrightarrow{KL}=\frac{1}{2}\overrightarrow{AC}.
3. En déduire que les \overrightarrow{IJ} ,\overrightarrow{KL} et \overrightarrow{AB} sont coplanaires.
Positions relatives de droites et de plans dans l’espace.
P est un plan de direction \overrightarrow{u},\overrightarrow{v} et d est une droite de direction \overrightarrow{w}.
\overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} sont coplanaires donc d et P sont parallèles.
\overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} ne sont pas coplanaires.
d est strictement parallèle à P.
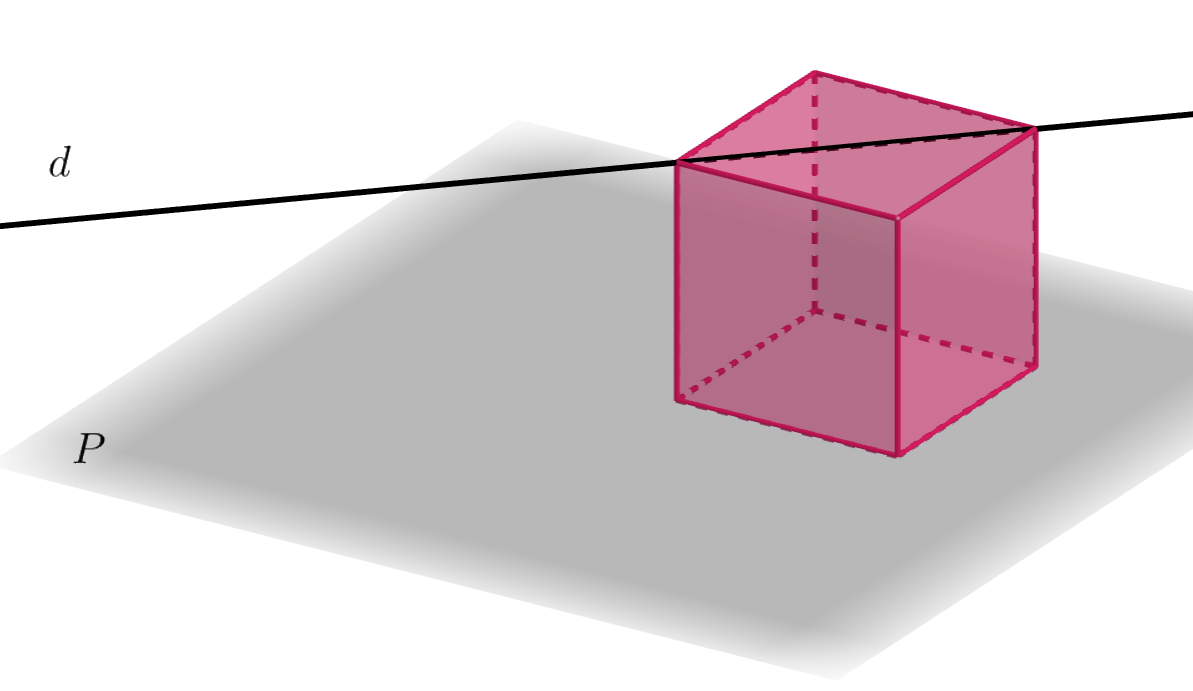
d est contenue dans P.
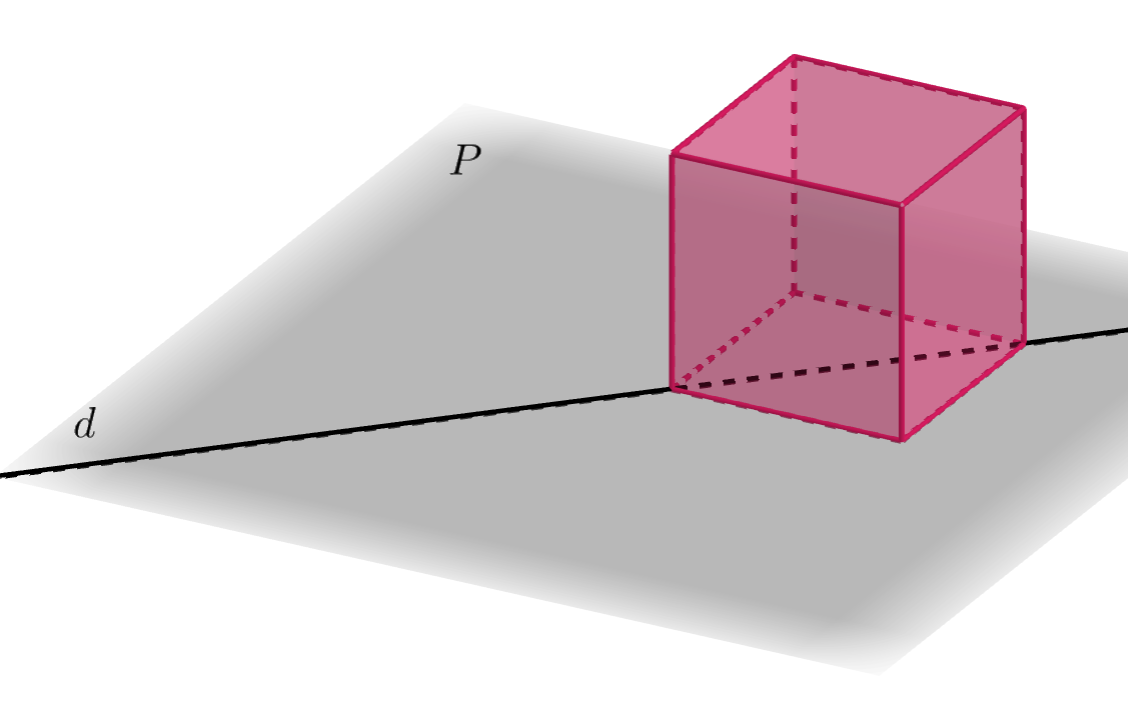
d et P sont sécants en M.
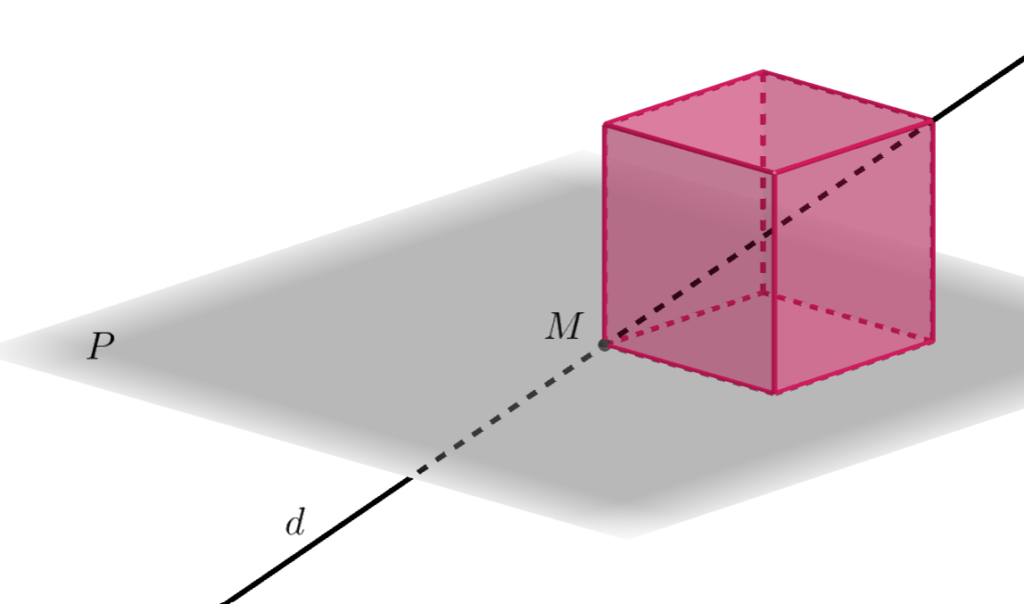
P et P’ sont deux plans.
P et P’ sont parallèles.
P et P’ n’ont pas la même direction.
P est strictement parallèle à P’.
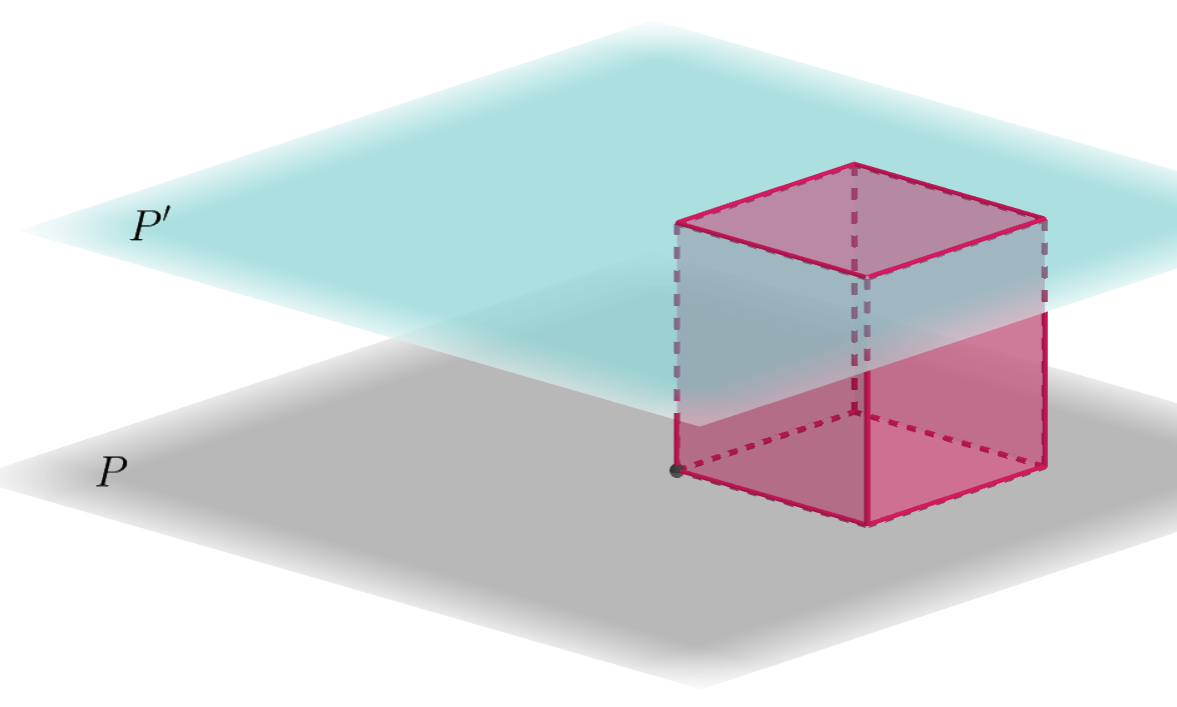
P et P’ sont confondus.
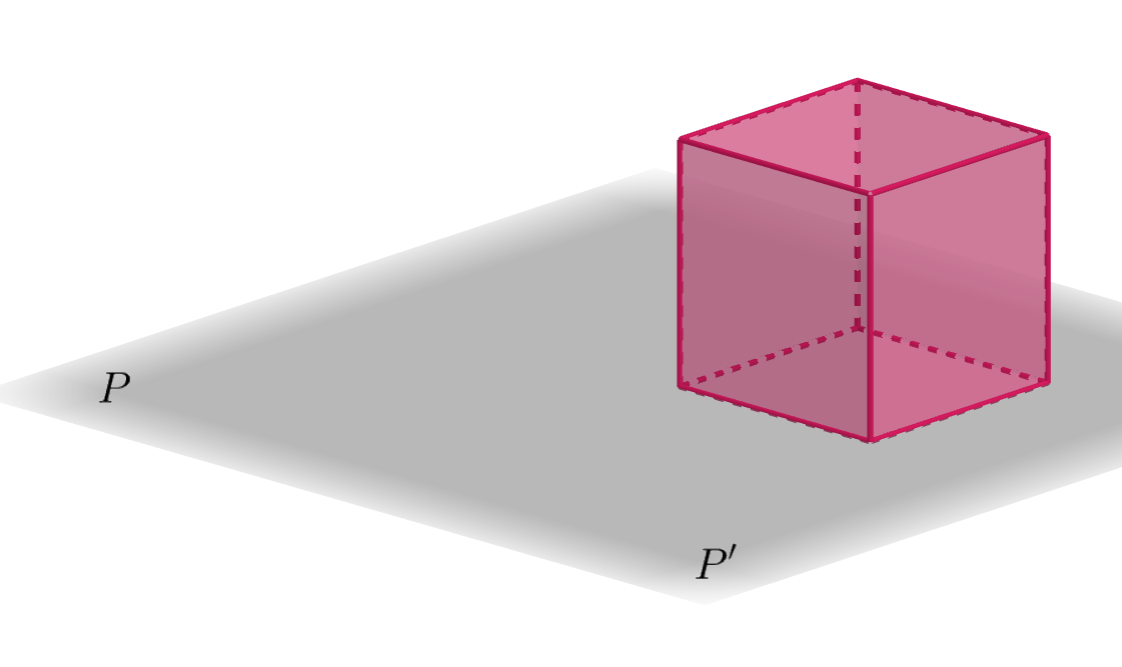
P et P’ sont sécants suivant une droite d.
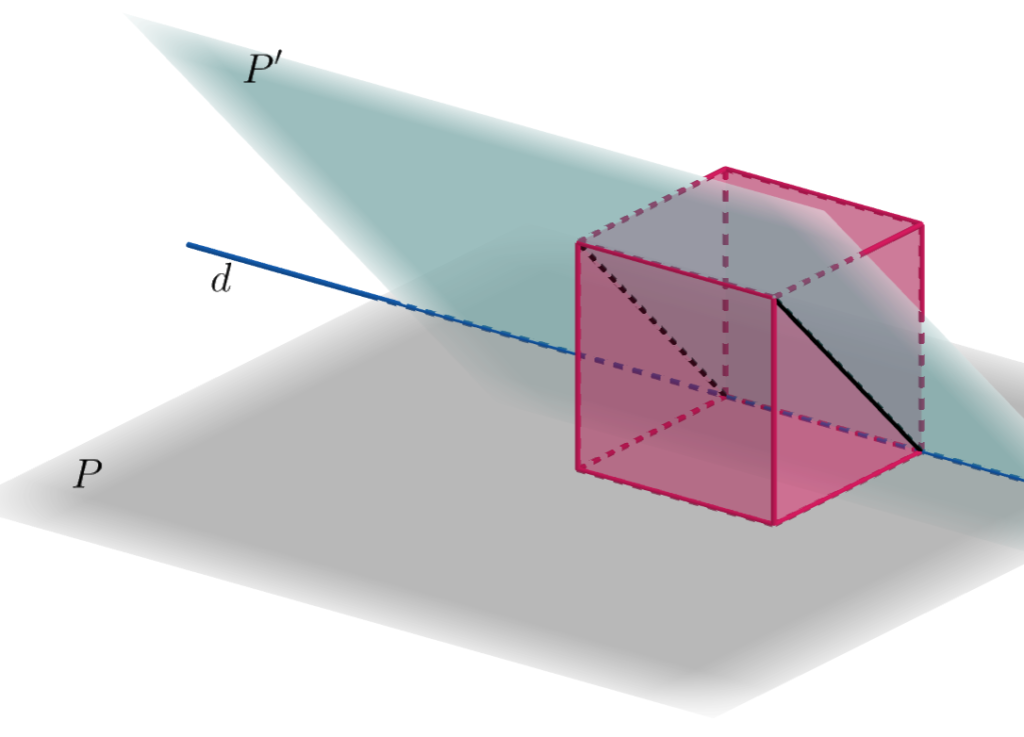
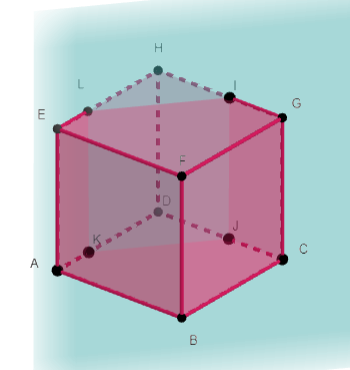
Exercice n°2
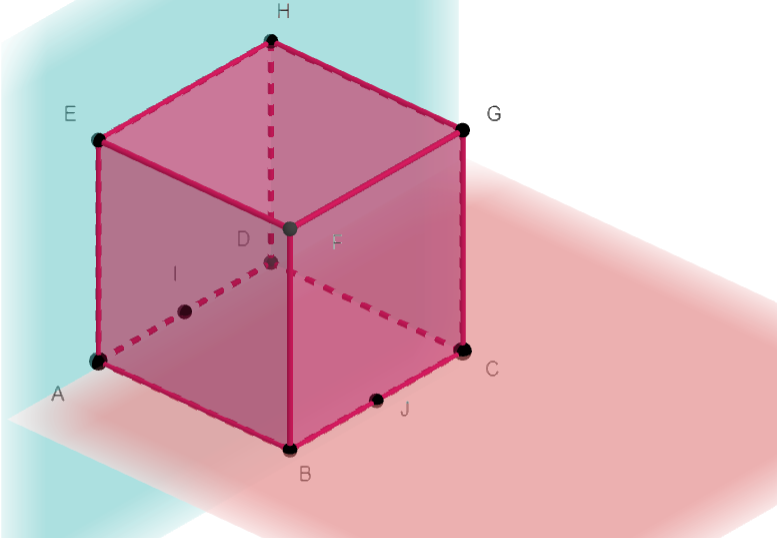
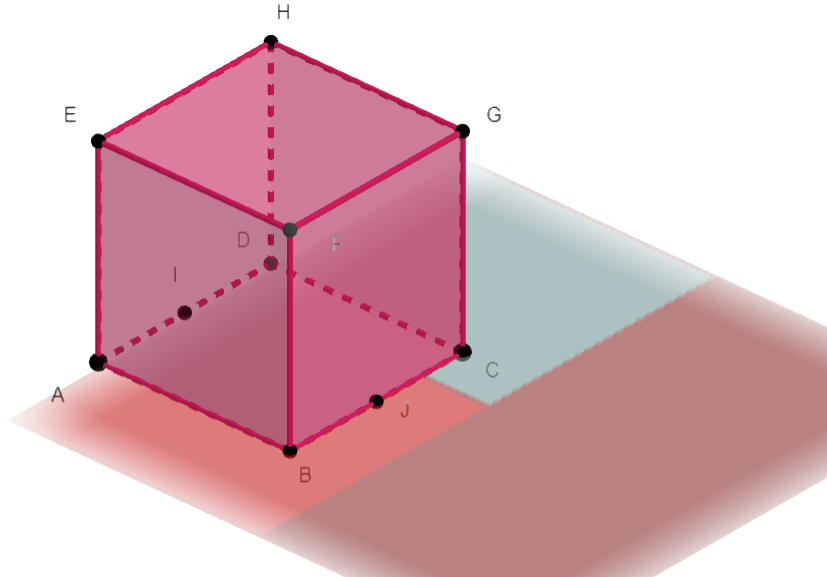
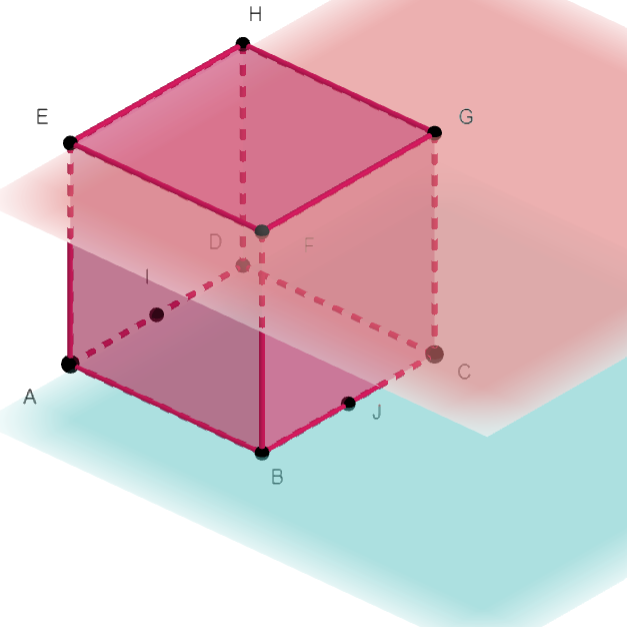
ABCDEFGH est un cube.
Les points I et J sont les milieux de [AD] et [BC].
Préciser la position des plans ci-dessous.
Pour tracer, par exemple, le plan (AIE) avec géogébra : cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par trois points dans le menu déroulant. Ensuite dans le repère, cliquer sur les trois points A,I,E.
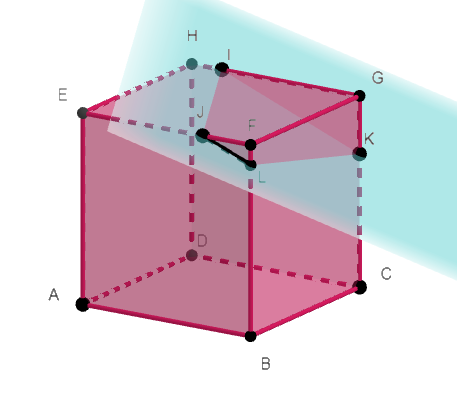
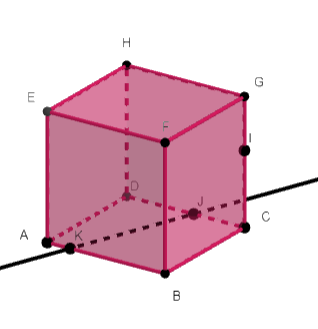
Exercice n°3
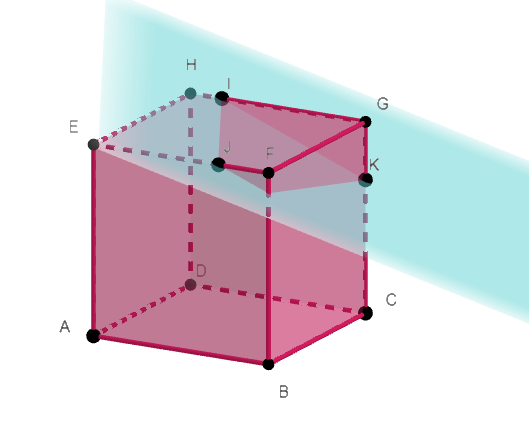
ABCDEFGH est un cube.
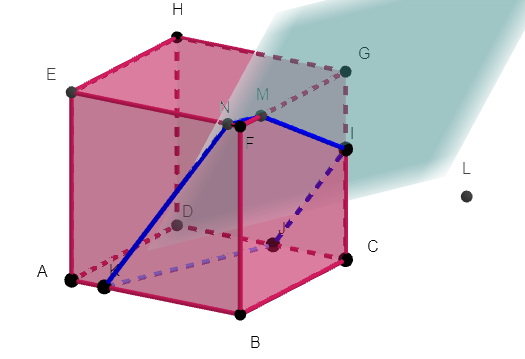
Les points I\in[HG], J\in[EF]et K\in[GC].
L’objectif est de tracer la section du cube ABCDEFGH par le plan (IJK).
1. tracer la droite d’intersection de la face EFGH par le plan (IJK) en justifiant.
2. tracer la droite d’intersection de la face CDHG par le plan (IJK) en justifiant.
3. tracer la droite d’intersection de la face ABFE par le plan (IJK) en justifiant.
4. tracer la droite d’intersection de la face BCGF par le plan (IJK) en justifiant.
5. répondre à la question posée dans l’exercice.
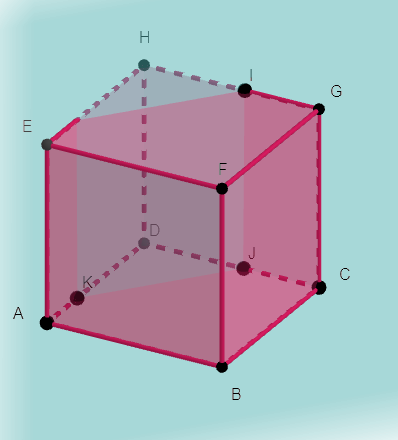
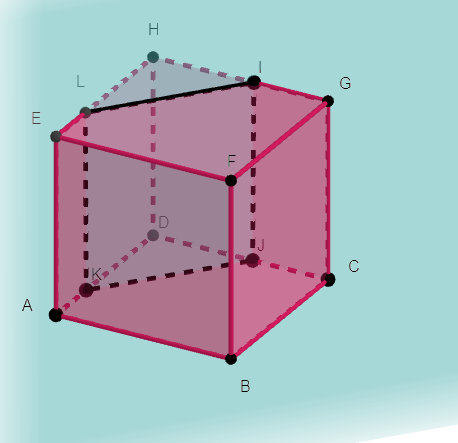
Exercice n°4
ABCDEFGH est un cube.
Les points I\in[HG], J\in[DC]et K\in[DA].
L’objectif est de tracer la section du cube ABCDEFGH par le plan (IJK).
1. tracer la droite d’intersection de la face ABCD par le plan (IJK) en justifiant.
2. tracer la droite d’intersection de la face DCGH par le plan (IJK) en justifiant.
3. tracer la droite d’intersection de la face EFGH par le plan (IJK) en justifiant.
4. tracer la droite d’intersection de la face AEHD par le plan (IJK) en justifiant.
5. répondre à la question posée dans l’exercice.
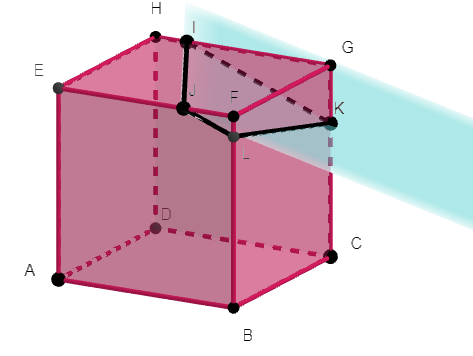
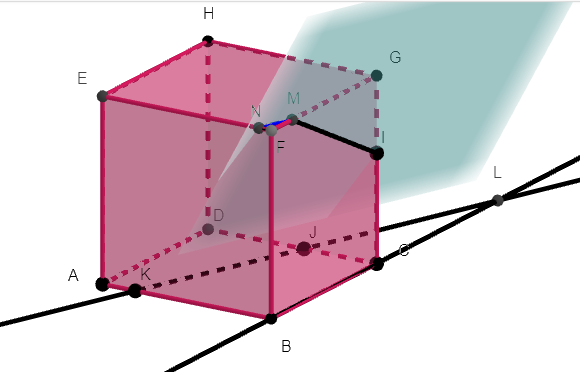
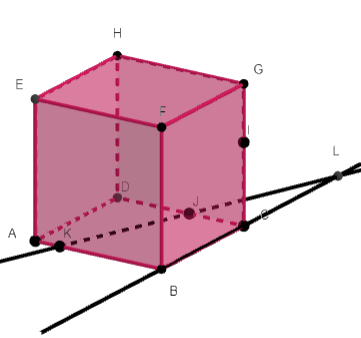
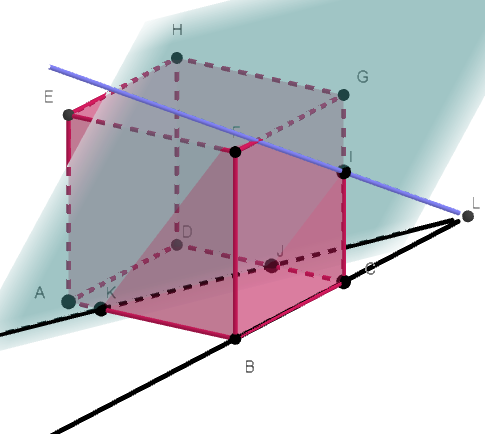
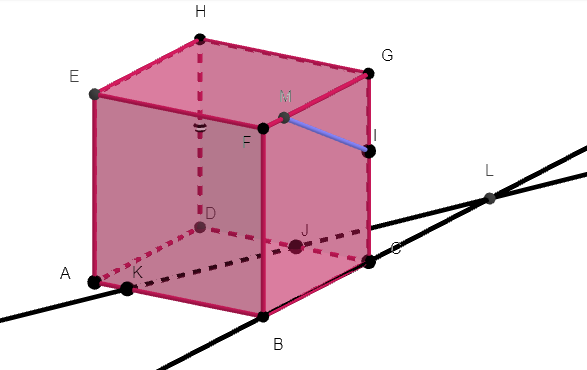
Exercice n°5
ABCDEFGH est un cube.
Les points I\in[HG], J\in[EF]et K\in[GC].
L’objectif est de tracer la section du cube ABCDEFGH par le plan (IJK).
1. a.tracer la droite d’intersection du plan (ABC) par le plan (IJK) en justifiant.
b. placer L le point d’intersection des droites (BC) et (KJ).
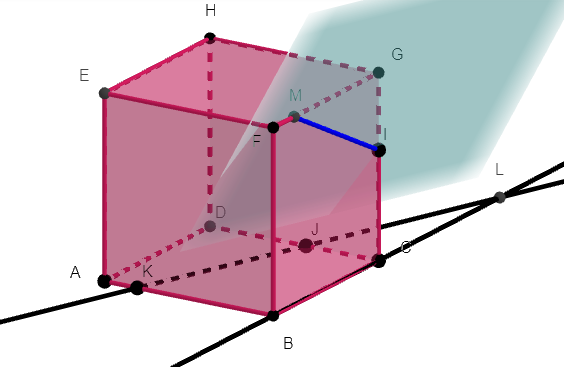
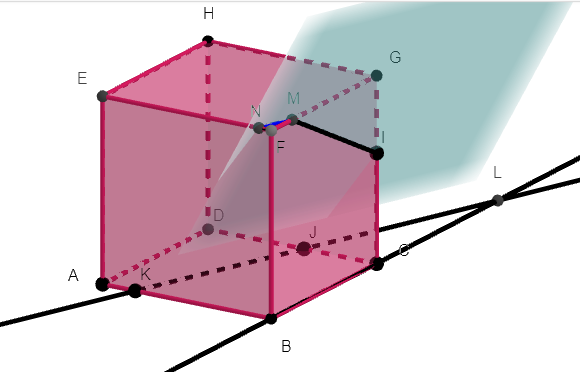
2.a. tracer la droite d’intersection du plan (BCF) et du plan (IJK) en justifiant.
2.b. En déduire l’intersection de la face BCFG et du plan (IJK) en justifiant.
3. tracer la droite d’intersection de la face DCGH par le plan (IJK) en justifiant.
4. tracer la droite d’intersection de la face EFGH par le plan (IJK) en justifiant.
5. tracer la droite d’intersection de la face ABFE par le plan (IJK) en justifiant.
6. répondre à la question posée dans l’exercice.