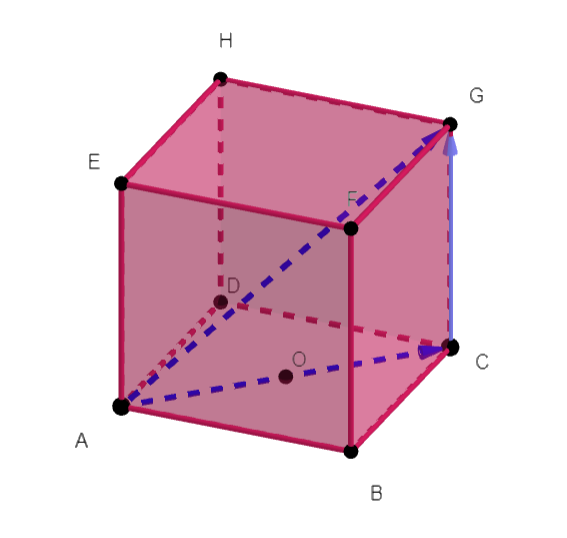
On considère un cube ABCDEFGH. Le point O est le centre de la face ABCD.
M est défini par \overrightarrow{OM}=\frac{1}{3}\overrightarrow{OE}.
1. Montrer que \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}.
2. Montrer que \overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}.
3. Que peut-on en conclure ?
On veut exprimer le vecteur \overrightarrow{AM} en fonction de vecteurs ne comportant que des points initiaux ou points de départ.
Il faut faire disparaître le point nouvellement construit M . Comme M apparaît dans l’énoncé dans l’égalité suivante : \overrightarrow{OM}=\frac{1}{3}\overrightarrow{OE} on va utiliser la relation de Chasles avec le point O.
\overrightarrow{AM}=\overrightarrow{AO}+\overrightarrow{OM}De cette façon, on peut remplacer \overrightarrow{OM} par \frac{1}{3}\overrightarrow{OE}
\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}\overrightarrow{OE}Dans l’égalité vectorielle qu’on veut démontrer : \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}, à droite du signe égal il y a les vecteurs \overrightarrow{AO} et \overrightarrow{AE}. On va donc remplacer \overrightarrow{OE} par \overrightarrow{OA}+\overrightarrow{AE} à l’aide de la relation de Chasles.
\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{AE})On développe.
\overrightarrow{AM}=\overrightarrow{AO}+\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{AE}Pour réduire on met au même dénominateur
\overrightarrow{AM}=\frac{3}{3}\overrightarrow{AO}-\frac{1}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}\\ \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}
On utilise la relation de Chasles :
\overrightarrow{AG}=\overrightarrow{AC}+\overrightarrow{CG}.
Comme O est le milieu de la diagonale [AC] , \overrightarrow{AC}=2\overrightarrow{AO}
\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{CG}De plus \overrightarrow{CG}=\overrightarrow{AE}, donc
\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}
On a montré à la question 1 :
\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE}On a montré à la question 2 :
\overrightarrow{AG}=2\overrightarrow{AO}+\overrightarrow{AE}Si on mutiplie l’égalité vectorielle \overrightarrow{AM}=\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{AE} par 3, on obtient :
3\overrightarrow{AM}=2\overrightarrow{AO}+\overrightarrow{AE}3\overrightarrow{AM} et \overrightarrow{AG} sont égaux au même troisième vecteur 2\overrightarrow{AO}+\overrightarrow{AE} donc:
3\overrightarrow{AM}=\overrightarrow{AG}
Donc les vecteurs \overrightarrow{AM} et \overrightarrow{AG} sont colinéaires.
Donc les points A,M et G sont alignés.
Réponse:
\overrightarrow{DC}=\overrightarrow{HG}.
Résoudre graphiquement f(x)=1
C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.
Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.
Les antécédents sont -2 et 2.
Donc S=\{-2;2\}
Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.
