logo

T. repères de l’espace

Sommaire

Base de l’espace

Définition

Une base de l’espace est formée d’un triplet de vecteurs (\overrightarrow{i}, \overrightarrow{j},\overrightarrow{k}) non coplanaires.

Exercice n°1

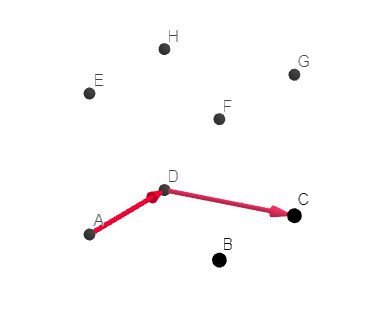
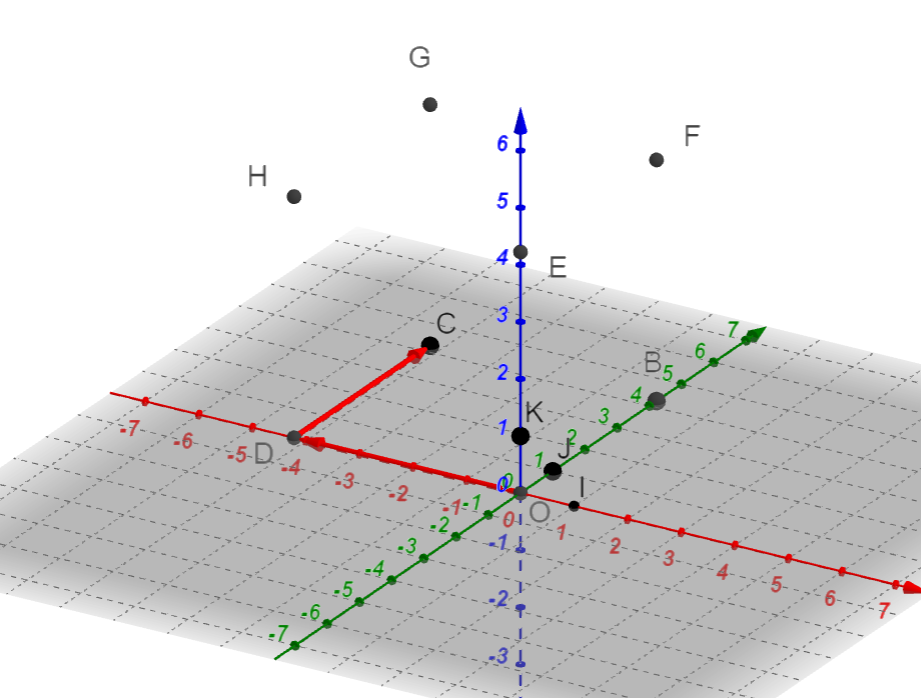
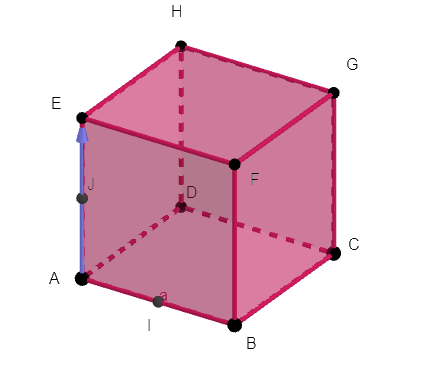
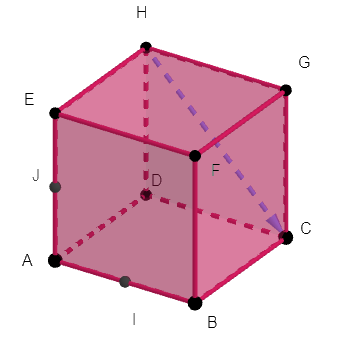
On considère le cube ABCDEFGH ci-contre. Parmi les triplets suivants lequel n’est pas une base ?

 a. (\overrightarrow{DA}, \overrightarrow{DB},\overrightarrow{DC})

b. (\overrightarrow{DA}, \overrightarrow{DC},\overrightarrow{DH}) 

correction

Propriété et définition

Soit (\overrightarrow{i}, \overrightarrow{j},\overrightarrow{k}) une base de l’espace.

Pour tout vecteur \overrightarrow{u} de l’espace, il existe un unique triplet  (x ; y ; z) tel que \overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}.

(x ; y ; z) sont les coordonnées de \overrightarrow{u} dans cette base. On note \overrightarrow{u}(x ; y ; z)

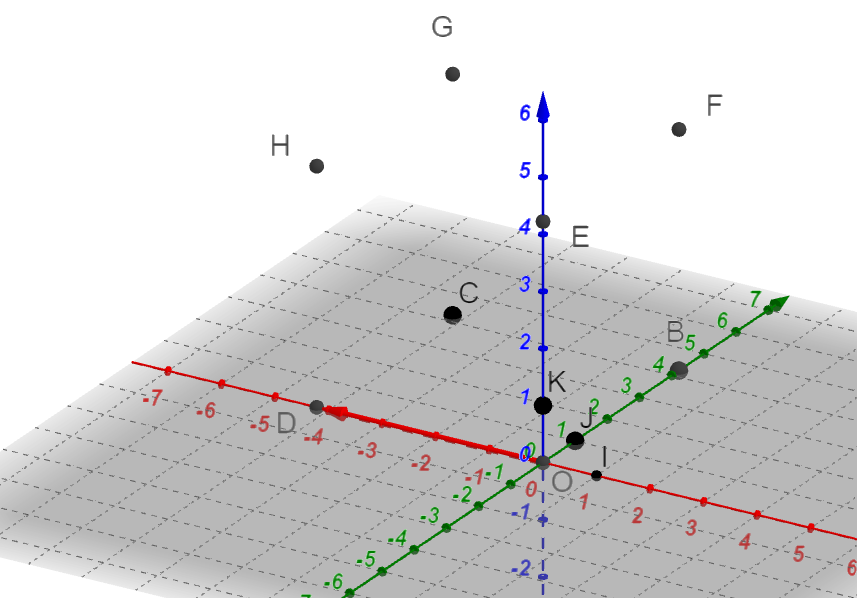
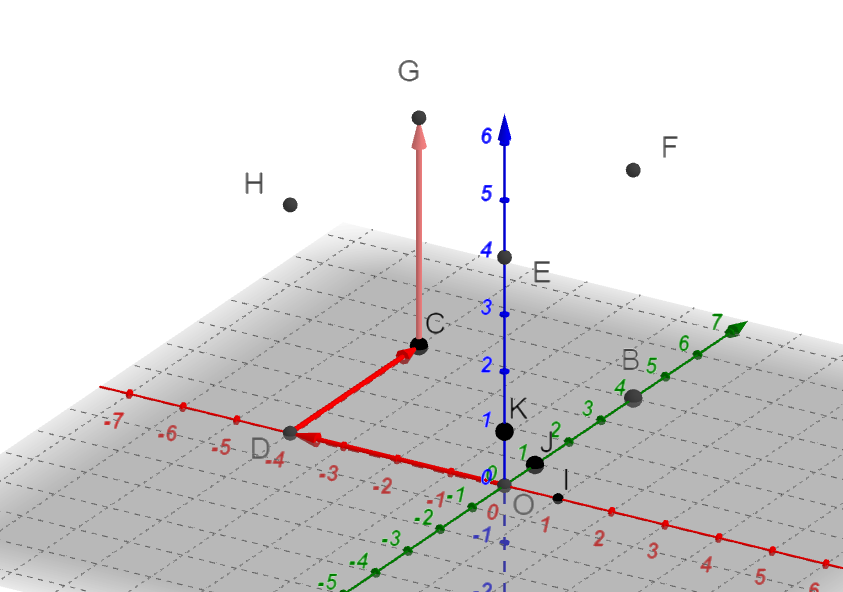
Exercice n°2

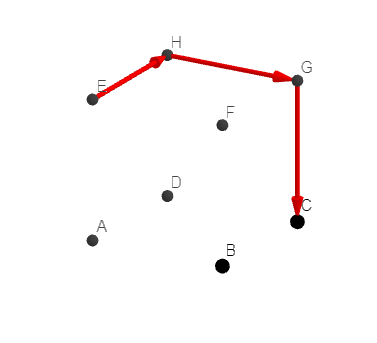
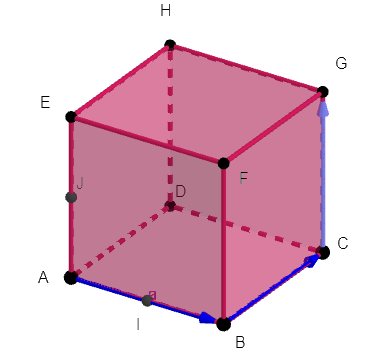
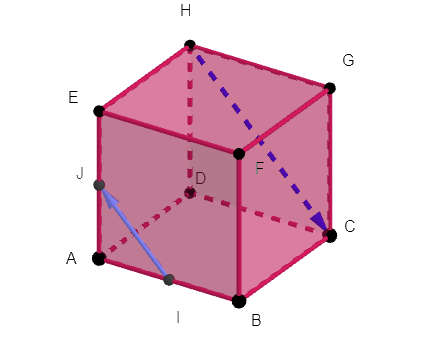
On considère le cube ABCDEFGH

Déterminer les coordonnées des vecteurs suivants dans la base (\overrightarrow{DA}, \overrightarrow{DC},\overrightarrow{DH}). 

a. \overrightarrow{AC}

correction

b. \overrightarrow{EC}

correction

c. \overrightarrow{DG}

correction

Repère de l’espace

Définition

Un repère de l’espace est formé d’un point O et d’une base (\overrightarrow{i}, \overrightarrow{j},\overrightarrow{k})

On note (O;\overrightarrow{i}; \overrightarrow{j};\overrightarrow{k}) un tel repère, O est l’origine du repère.

Remarque 

L’origine du repère O a pour coordonnées (0;0;0)..

Propriété et définition

Soit (O;\overrightarrow{i}; \overrightarrow{j};\overrightarrow{k}) un repère de l’espace.

Pour tout point M de l’espace, il existe un unique triplet  (x ; y ; z) tel que \overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}.

(x ; y ; z) sont les coordonnées du point  M dans ce repère. 

x est l’abscisse de M.

y est l’ordonnée de M.

z est la cote de M.

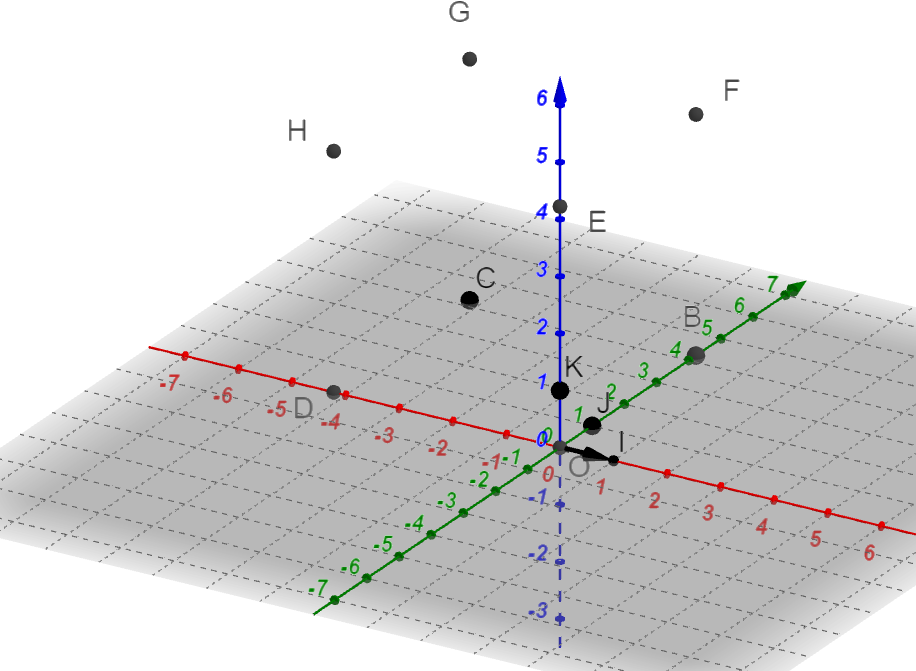
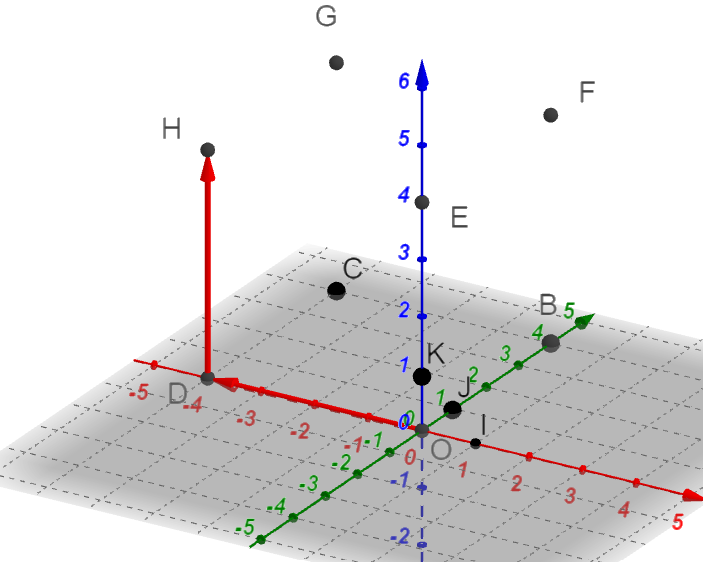
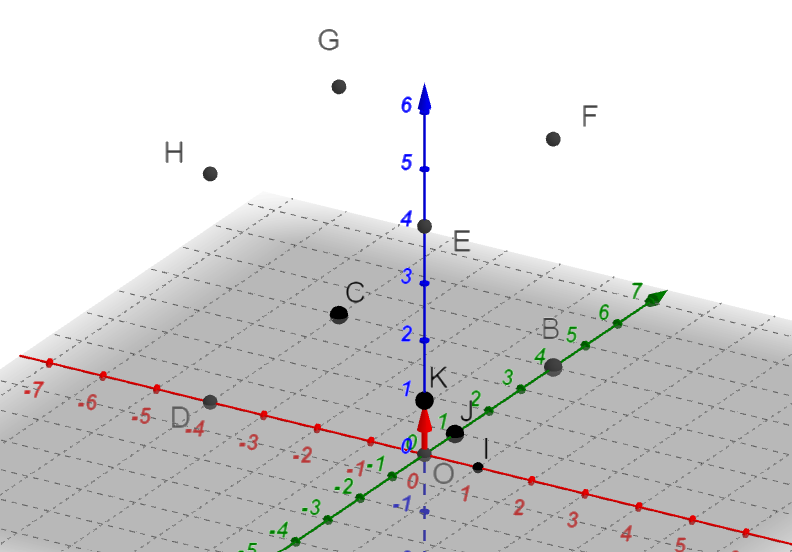
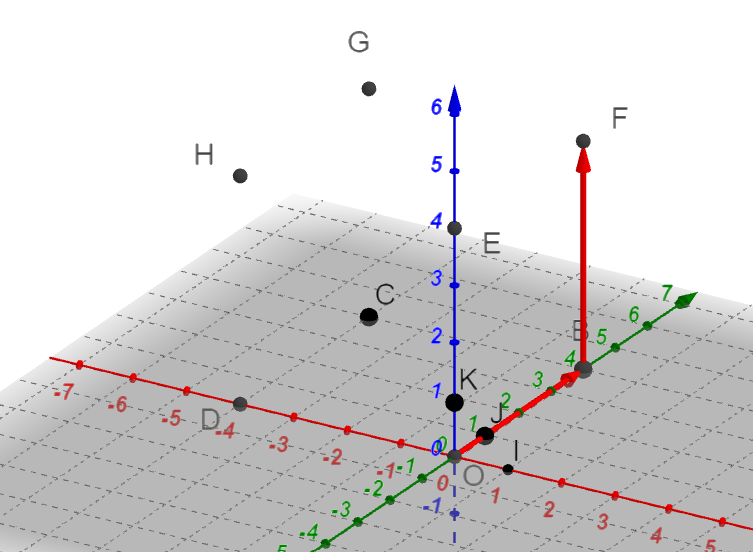
Exercice n°3

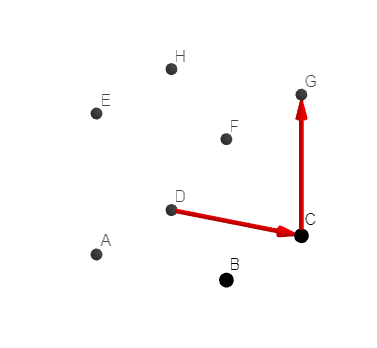
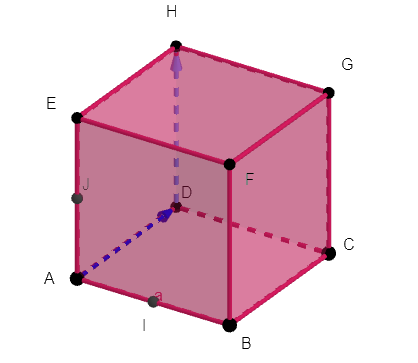
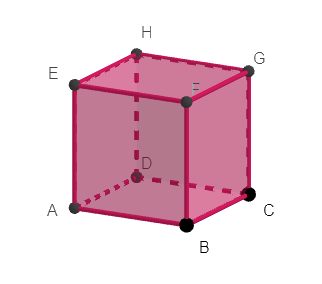
On considère le cube OBCDEFGH

Déterminer les coordonnées des points suivants dans le repère (O;\overrightarrow{OI}, \overrightarrow{OJ},\overrightarrow{OK}). 

a. B

correction

b. C

correction

c. I

correction

d. D

correction

e. G

correction

f. H

correction

g. K

correction

h. F

correction

Propriétés 

Soit (O;\overrightarrow{i}; \overrightarrow{j};\overrightarrow{k}) un repère de l’espace.

Soient  \overrightarrow{u}(x;y;z) et \overrightarrow{v}(x’;y’;z’) deux vecteurs de l’espace,  k est un réel et   A(x_A;y_A;z_A) et  B(x_B;y_B;z_B) deux points de l’espace.

  • Le milieu du segment [AB] a pour coordonnées  \frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2}; \frac{z_A+z_B}{2}. 
  • Dans la base (\overrightarrow{i}; \overrightarrow{j};\overrightarrow{k}):

\overrightarrow{u}+\overrightarrow{v}(x+x’;y+y’;z+z’)          k\overrightarrow{u}(kx;ky;kz)        \overrightarrow{AB}(x_B-x_A;y_B-y_A;z_B-z_A) 

  • \overrightarrow{u} et \overrightarrow{v} sont colinéaires si et seulement si leurs coordonnées sont proportionnelles..

Exercice n°4

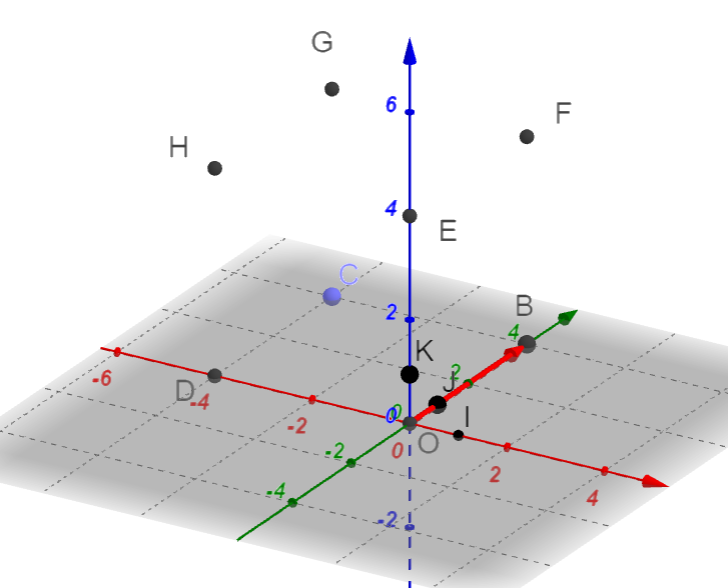
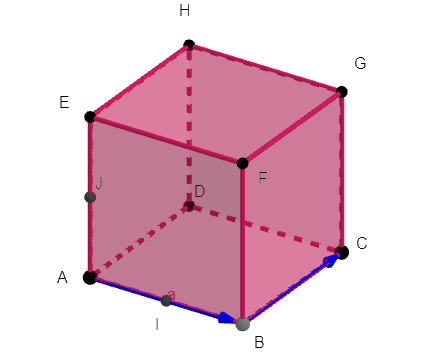
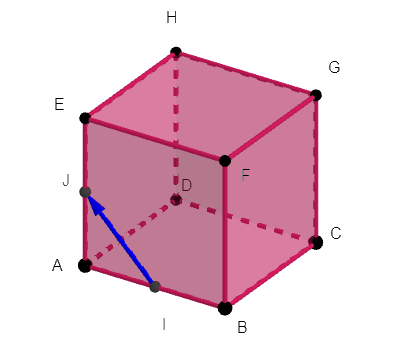
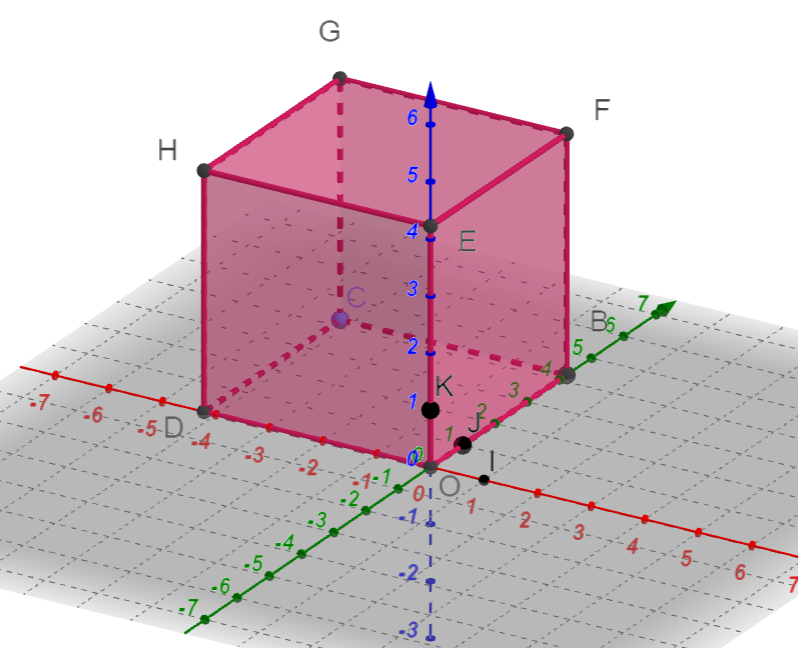
ABCDEFGH est un cube.

Les points I et J sont les milieux respectifs de  [AB] et [AE].

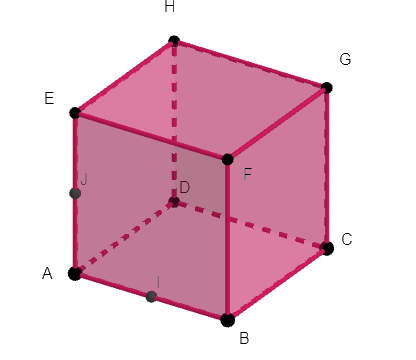
On choisit le repère A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}

1. Lire graphiquement les coordonnées des points C,E,F,G,H. 

correction C
correction E
correction F
correction G
correction H

2. Déterminer par le calcul les coordonnées des points I et J.

correction de I
correction de J

3. a. Calculer les coordonnées du vecteur \overrightarrow{IJ}.

correction

3. b. Calculer les coordonnées du vecteur \overrightarrow{HC}.

correction

3.c. Montrer que les vecteurs  \overrightarrow{HC} et \overrightarrow{IJ} sont colinéaires.

correction

©2020 – Math’O karé SAS

On considère le cube ABCDEFGH ci-contre. 

(\overrightarrow{DA}, \overrightarrow{DB},\overrightarrow{DC}) n’est pas un base car les vecteurs \overrightarrow{DA}, \overrightarrow{DB},\overrightarrow{DC} sont coplanaires.

En revanche, (\overrightarrow{DA}, \overrightarrow{DC},\overrightarrow{DH}) est une base car le point H n’appartient pas au plan (ADC).

Pour décomposer le vecteur \overrightarrow{AC}, il faut :

Partir du point A ( l’origine du vecteur \overrightarrow{AC}) pour se rendre au point C ( l’extrémité du vecteur \overrightarrow{AC}) en se déplaçant d’abord suivant la direction du premier vecteur de la base ( ici \overrightarrow{DA}) puis suivant la direction du deuxième vecteur de la base ( ici \overrightarrow{DC}) et enfin suivant la direction du troisième vecteur de la base ( ici \overrightarrow{DH}).

On part de  A, on se déplace de  (-1)\times\overrightarrow{DA} puis de  1\times\overrightarrow{DC} et de  0\times\overrightarrow{DH}. 

Donc \overrightarrow{AC}(-1;1;0) dans la base (\overrightarrow{DA};\overrightarrow{DC}; \overrightarrow{DH}).

 

Pour décomposer le vecteur \overrightarrow{EC}, il faut :

Partir du point E ( l’origine du vecteur \overrightarrow{EC}) pour se rendre au point C ( l’extrémité du vecteur \overrightarrow{EC}) en se déplaçant d’abord suivant la direction du premier vecteur de la base ( ici \overrightarrow{DA}) puis suivant la direction du deuxième vecteur de la base ( ici \overrightarrow{DC}) et enfin suivant la direction du troisième vecteur de la base ( ici \overrightarrow{DH}).

On part de  E, on se déplace de  (-1)\times\overrightarrow{DA} puis de  1\times\overrightarrow{DC} et de  (-1)\times\overrightarrow{DH}. 

Donc \overrightarrow{EC}(-1;1;-1) dans la base (\overrightarrow{DA};\overrightarrow{DC}; \overrightarrow{DH}).

Pour décomposer le vecteur \overrightarrow{DG}, il faut :

Partir du point D ( l’origine du vecteur \overrightarrow{DG}) pour se rendre au point G ( l’extrémité du vecteur \overrightarrow{DG}) en se déplaçant d’abord suivant la direction du premier vecteur de la base ( ici \overrightarrow{DA}) puis suivant la direction du deuxième vecteur de la base ( ici \overrightarrow{DC}) et enfin suivant la direction du troisième vecteur de la base ( ici \overrightarrow{DH}).

On part de  D, on se déplace de  0\times\overrightarrow{DA} puis de  1\times\overrightarrow{DC} et de  1\times\overrightarrow{DH}. 

Donc \overrightarrow{DG}(0;1;1) dans la base (\overrightarrow{DA};\overrightarrow{DC}; \overrightarrow{DH}).

Pour déterminer les coordonnées du point B, il faut :

Partir de l’origine  O  pour se rendre au point B  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  0\times\overrightarrow{OI} puis de  4\times\overrightarrow{OJ} et de  0\times\overrightarrow{OK}. 

Donc B(0;4;0) dans le repère  (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point C, il faut :

Partir de l’origine  O  pour se rendre au point C  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  -4\times\overrightarrow{OI} puis de  4\times\overrightarrow{OJ} et de  0\times\overrightarrow{OK}. 

Donc C(-4;4;0) dans le repère  (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point I, il faut :

Partir de l’origine  O  pour se rendre au point I  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  1\times\overrightarrow{OI} puis de  0\times\overrightarrow{OJ} et de  0\times\overrightarrow{OK}. 

Donc I(1;0;0) dans le repère  (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point D, il faut :

Partir de l’origine  O  pour se rendre au point D  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  -4\times\overrightarrow{OI} puis de  0\times\overrightarrow{OJ} et de  0\times\overrightarrow{OK}. 

Donc D(-4;0;0) dans le repère  (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point G, il faut :

Partir de l’origine  O  pour se rendre au point G  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  -4\times\overrightarrow{OI} puis de  4\times\overrightarrow{OJ} et de  4\times\overrightarrow{OK}. 

Donc G(-4;4;4) dans le repère (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point H, il faut :

Partir de l’origine  O  pour se rendre au point H  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  -4\times\overrightarrow{OI} puis de  0\times\overrightarrow{OJ} et de  4\times\overrightarrow{OK}. 

Donc H(-4;0;4) dans le repère (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point K, il faut :

Partir de l’origine  O  pour se rendre au point K  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  0\times\overrightarrow{OI} puis de  0\times\overrightarrow{OJ} et de  1\times\overrightarrow{OK}. 

Donc K(0;0;1) dans le repère (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point F, il faut :

Partir de l’origine  O  pour se rendre au point F  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{OI}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{OJ}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{OK}).

On part de  O, on se déplace de  0\times\overrightarrow{OI} puis de  4\times\overrightarrow{OJ} et de  4\times\overrightarrow{OK}. 

Donc F(0;4;4) dans le repère (O; \overrightarrow{OI};\overrightarrow{OJ}; \overrightarrow{OK}).

Pour déterminer les coordonnées du point C, il faut :

Partir de l’origine  A  pour se rendre au point C  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE}. 

Donc C(1:1;0) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point E, il faut :

Partir de l’origine  A  pour se rendre au point E  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  0\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc E(0;0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point F, il faut :

Partir de l’origine  A  pour se rendre au point F  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc F(1;0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point G, il faut :

Partir de l’origine  A  pour se rendre au point G  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc G(1;1;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point H, il faut :

Partir de l’origine  A  pour se rendre au point H  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc H(0;1;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

A(0;0;0) et B(1;0;0)

Pour déterminer les coordonnées du point I milieu de [AB] : on remplace x_A, y_A et z_A par 0 et x_B par 1 , y_B par 0 et z_B par 0 dans :

 x_I=\frac{x_A+x_B}{2} ;  y_I=\frac{y_A+y_B}{2} et  z_I=\frac{z_A+z_B}{2}

 x_I=\frac{0+1}{2} ;  y_I=\frac{0+0}{2} et  z_I=\frac{0+0}{2}

 x_I=\frac{1}{2} ;  y_I=0 et  z_I=0

Donc  I(\frac{1}{2};0;0)

 

A(0;0;0) et E(0;0;1)

Pour déterminer les coordonnées du point J milieu de [AE] : on remplace x_A, y_A et z_A par 0 et x_E par 0 , y_E par 0 et z_E par 1 dans :

 x_J=\frac{x_A+x_E}{2} ;  y_J=\frac{y_A+y_E}{2} et  z_J=\frac{z_A+z_E}{2}

 x_J=\frac{0+0}{2} ;  y_J=\frac{0+0}{2} et  z_J=\frac{0+1}{2}

 x_J=0 ;  y_J=0 et  z_J=\frac{1}{2}

Donc  J(0;0;\frac{1}{2})

On veut déterminer les coordonnées du point I défini par \overrightarrow{EI}=\frac{1}{3}\overrightarrow{EF}

Pour déterminer les coordonnées du vecteur  \overrightarrow{IJ} : on remplace x_I par \frac{1}{2}  , y_I par 0 et z_I par 0 puis  x_J par 0 , y_J par 0 et z_J par par \frac{1}{2}dans :

\overrightarrow{IJ}(x_J-x_I; y_J-y_I; z_J-z_I)

\overrightarrow{IJ}(0-\frac{1}{2}; 0-0; \frac{1}{2}-0)

\overrightarrow{IJ}(-\frac{1}{2}; 0; \frac{1}{2})

I(\frac{1}{2};0;0) et J(0;0;\frac{1}{2}). 

Pour déterminer les coordonnées du vecteur  \overrightarrow{IJ} : on remplace x_I par \frac{1}{2}  , y_I par 0 et z_I par 0 puis  x_J par 0 , y_J par 0 et z_J par par \frac{1}{2}dans :

\overrightarrow{IJ}(x_J-x_I; y_J-y_I; z_J-z_I)

\overrightarrow{IJ}(0-\frac{1}{2}; 0-0; \frac{1}{2}-0)

\overrightarrow{IJ}(-\frac{1}{2}; 0; \frac{1}{2})

 

H(0;1;1) et C(1;1;0). 

Pour déterminer les coordonnées du vecteur  \overrightarrow{HC} : on remplace x_H par 0  , y_H par 1 et z_H par 1 puis  x_C par 1 , y_C par 1 et z_C par par 0dans :

\overrightarrow{HC}(x_C-x_H; y_C-y_H; z_C-z_H)

\overrightarrow{HC}(1-0; 1-1; 0-1)

\overrightarrow{HC}(1; 0; -1)

 

On a montré que : \overrightarrow{IJ}(-\frac{1}{2}; 0; \frac{1}{2}) et \overrightarrow{HC}(1; 0; -1).

Pour montrer que les vecteurs \overrightarrow{IJ} et \overrightarrow{HC} sont colinéaires, il faut montrer que leurs coordonnées sont proportionnelles.

\overrightarrow{IJ}

-\frac{1}{2}0\frac{1}{2}

\overrightarrow{HC}

10-1

On multiplie par -2 les nombres du haut pour obtenir les nombres du bas

Le tableau ci-dessus est un tableau de proportionnalité donc les coordonnées des vecteurs \overrightarrow{IJ} et \overrightarrow{HC} sont proportionnelles.

Ainsi les vecteurs \overrightarrow{IJ} et \overrightarrow{HC} sont colinéaires.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.