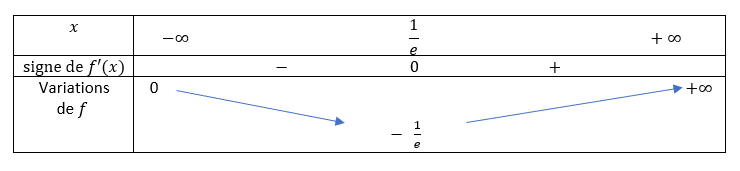
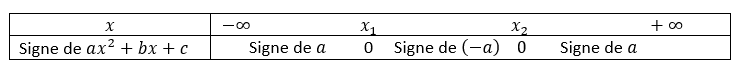1. Dérivée et variations
Propriétés :
La fonction logarithme népérien est continue et dérivable sur ]0;+\infty[ et pour tout x \in ]0;+\infty[ , ln'(x)=\frac{1}{x}.
Soit u une fonction dérivable sur un intervalle I, telle que, pour tout x\in I , u(x)>0.
La fonction ln\circ u : x\to ln (u(x)) est dérivable sur I et (ln\circ u)’= \frac{u’}{u}.
Exercice n°1 :
Calculer f'(x) dans chaque cas.
On peut utiliser la fenêtre active Géogébra ci-dessous pour conjecturer le résultat de la question 1 , saisir f(x)=\frac{1}{x}-2ln(x) puis cliquer sur le 9ème onglet ( f’ ).
S’affiche alors : Dérivée : f'(x)=\frac{-2}{x}-\frac{1}{x^2}
- f(x)=\frac{1}{x}-2ln(x)
pour x \in ]0;+\infty[
2. f(x)=2xln(x)
pour x \in ]0;+\infty[
3. f(x)=ln(2x^2+1)
pour x \in \mathbf{R}
4. f(x)=(x-2)ln(3x)
pour x \in ]0;+\infty[
5. f(x)=\frac{2ln(x)+1}{x}
pour x \in ]0;+\infty[
6. f(x)=ln^3(x)
pour x \in ]0;+\infty[
7. f(x)=\frac{2ln(x)-2}{x^2}
pour x \in ]0;+\infty[
8. f(x)=ln(\frac{x-2}{x+2})
pour x \in ]2;+\infty[
9. f(x)=ln(\frac{x^2}{x+2})
pour x \in ]-2;+\infty[
Propriété :
La fonction logarithme népérien est strictement croissante sur ]0;+\infty[.
Conséquence n°1 :
Pour tous réels a et b appartenant à ]0;+\infty[:
ln(a)=ln(b) \iff a=b
Exercice n°2 :
Résoudre les équations suivantes (ne pas oublier de déterminer l’ensemble d’existence à chaque fois).
On peut utiliser la fenêtre active Géogébra ci-dessous pour conjecturer le résultat de la question 1 , saisir ln(2-2x)=ln(4+2x)) puis cliquer sur le 7ème onglet (X= ).
S’affiche alors : Résoudre : \{x=\frac{-1}{2}\}
Conséquence n°2 :
Pour tous réels a et b appartenant à ]0;+\infty[:
ln(a)\leq ln(b) \iff a\leq b
Exercice n°3 :
Résoudre les inéquations suivantes (ne pas oublier de déterminer l’ensemble d’existence à chaque fois).
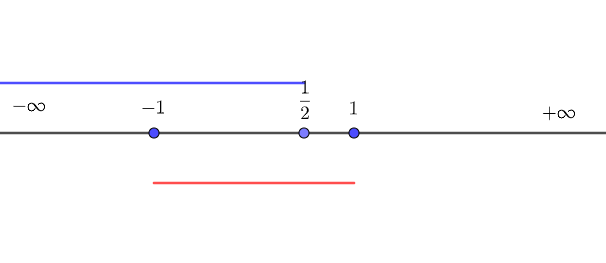
On peut utiliser la fenêtre active Géogébra de l’exercice n°2 pour conjecturer le résultat de la question 1 , saisir ln(3-3x)>ln(1+x)) puis cliquer sur le 7ème onglet (X= ).
S’affiche alors : Résoudre : \{-1<x<\frac{1}{2}\}
2. Limites
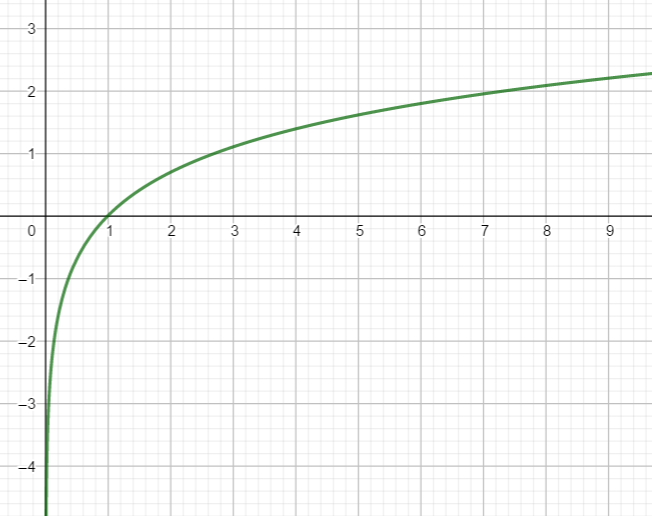
Propriétés :
lim_{x\to 0}\hspace{0.2cm}ln(x)=-\infty
lim_{x\to {+\infty}}\hspace{0.2cm}ln(x)=+\infty
Conséquences :
La courbe de la fonction logarithme népérien admet une asymptote verticale d’équation x=0.
Le tableau de la fonction ln est le suivant :

Exercice n°4 :
Calculer les limites suivantes
- lim_{x\to +\infty}\hspace{0.2cm}xln(x)
2. lim_{x\to 0}\hspace{0.2cm}x^3-3ln(x)
3. lim_{x\to +\infty}\hspace{0.2cm}ln(\frac{3+x}{x+1})
4. lim_{x\to -\infty}\hspace{0.2cm}ln(2-x)
5. lim_{x\to +\infty}\hspace{0.2cm}(ln(x))^2-ln(x)-1
6. lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{ln(x)-1}
Propriétés ( croissances comparées ) :
lim_{x\to +\infty}\frac{ln(x)}{x}=0\\lim_{x\to 0}xln(x)=0Pour tout entier naturel n\geq 2 , lim_{x\to +\infty}\frac{ln(x)}{x^n}=0 et lim_{x\to 0}x^nln(x)=0
Exercice n°5 :
Calculer les limites suivantes
1. lim_{x\to +\infty}\hspace{0.2cm}\frac{ln(x)-2}{x}
2. lim_{x\to +\infty}\hspace{0.2cm}ln(x)-x
3. lim_{x\to +\infty}\hspace{0.2cm}\frac{ln(2+x)}{x}
4. lim_{x\to 0}\hspace{0.2cm}\frac{xln(x)}{x^2+1}
Exercice n°6 :
Soit la fonction définie sur ]2;+\infty[ par f(x)=ln(2x-4).
- Calculer lim_{x\to 2}f(x) et lim_{x\to +\infty}f(x).
2.a. Calculer f'(x).
2.b. Etudier le signe de f'(x) sur ]2;+\infty[.
2.c. Dresser le tableau de variations de f sur ]2;+\infty[.
Exercice n°7 :
Soit la fonction définie sur ]0;+\infty[ par f(x)=xln(x).
- Calculer lim_{x\to 0}f(x) et lim_{x\to +\infty}f(x).
2.a. Calculer f'(x).
2.b. Etudier le signe de f'(x) sur ]0;+\infty[.
2.c. Dresser le tableau de variations de f sur ]0;+\infty[.
Exercice n°8 :
Soit la fonction définie sur ]0;+\infty[ par f(x)=\frac{ln(x)}{x}.
- Calculer lim_{x\to 0}f(x) et lim_{x\to +\infty}f(x).
2.a. Calculer f'(x).
2.b. Etudier le signe de f'(x) sur ]0;+\infty[.
2.c. Dresser le tableau de variations de f sur ]0;+\infty[.
Exercice n°9 :
Soit la fonction définie sur ]0;+\infty[ par f(x)=(ln(x))^2-ln(x)-1.
- Calculer lim_{x\to 0}f(x) et lim_{x\to +\infty}f(x).
2.a. Calculer f'(x).
2.b. Etudier le signe de f'(x) sur ]0;+\infty[.
2.c. Dresser le tableau de variations de f sur ]0;+\infty[.