Sommaire
Produit scalaire à l’espace
On étend aux vecteurs de l’espace la définition du produit scalaire dans le plan vue en classe de première.
Définition
\overrightarrow{u} et \overrightarrow{v} sont deux vecteurs de l’espace.
A;B;C sont trois points de l’espace tels que \overrightarrow{u}=\overrightarrow{AB} et \overrightarrow{v}=\overrightarrow{AC}.
Il existe au moins un plan P contenant les points A;B;C.
Le produit scalaire des vecteurs \overrightarrow{u} et \overrightarrow{v} noté \overrightarrow{u}.\overrightarrow{v} est le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} calculé dans le plan P.
Définition
Le produit scalaire d’un vecteur \overrightarrow{u} par un vecteur \overrightarrow{v} est le nombre réel \overrightarrow{u}.\overrightarrow{v} qui se lit \overrightarrow{u} scalaire \overrightarrow{v}.
Si \overrightarrow{u}=\overrightarrow{AB} et \overrightarrow{v}=\overrightarrow{AC} alors \overrightarrow{u}.\overrightarrow{v}= \overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC})
Si \overrightarrow{u}=\overrightarrow{0} ou \overrightarrow{v}=\overrightarrow{0} alors \overrightarrow{u}.\overrightarrow{v}=0 .
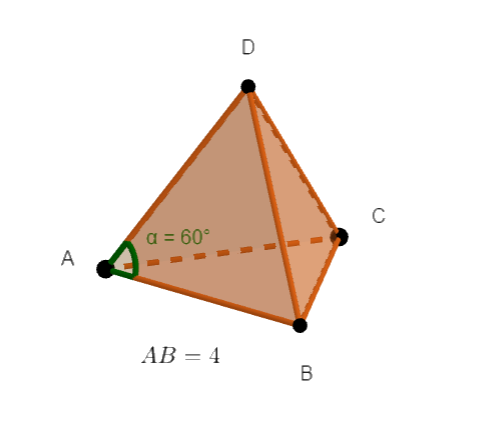
Exercice n°1
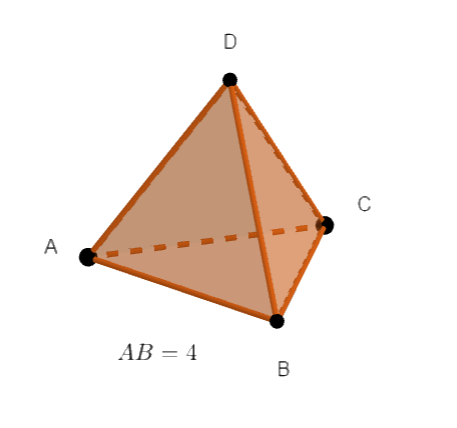
En utilisant la définition ci-dessus, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AD}.
Propriété
\overrightarrow{u}=\overrightarrow{AB} et \overrightarrow{v}=\overrightarrow{AC} sont deux vecteurs non nuls de l’espace.
On projette les points A et C sur la droite (AB). A projette en A et C se projette en H.
\overrightarrow{u}.\overrightarrow{v}=AB \times AHcar les vecteurs \overrightarrow{AB} et \overrightarrow{AH} ont même sens.
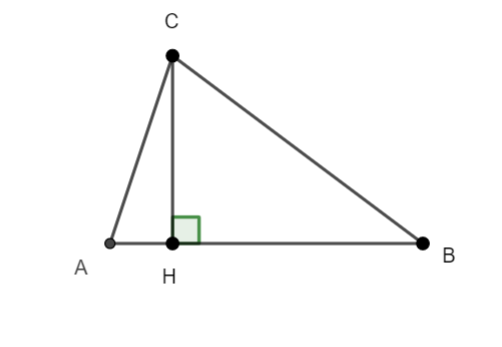
On projette les points A et C sur la droite (AB). A projette en A et C se projette en H.
\overrightarrow{u}.\overrightarrow{v}=-AB \times AHcar les vecteurs \overrightarrow{AB} et \overrightarrow{AH} sont de sens contraire.
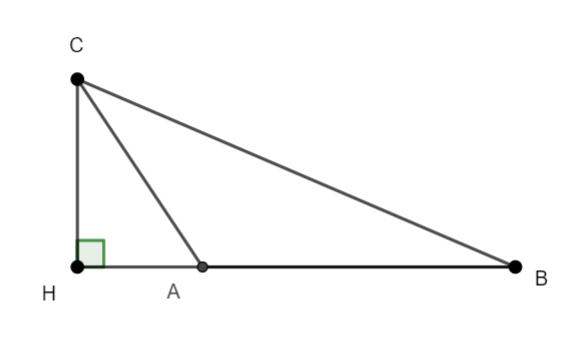
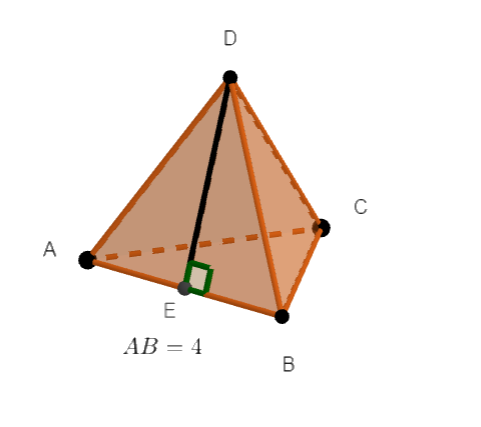
Exercice n°2

En utilisant la propriété ci-dessus, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AD}.
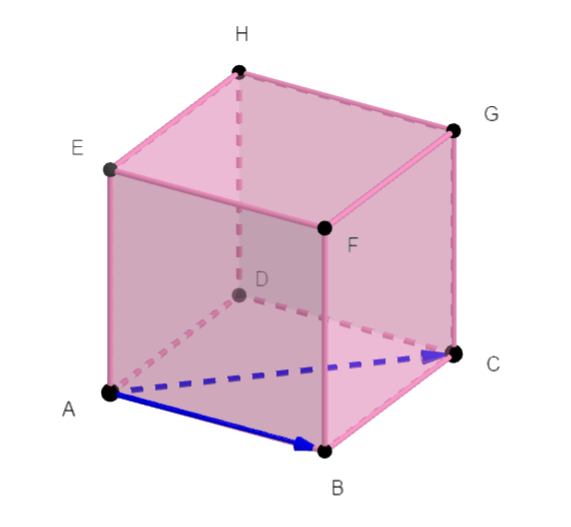
Exercice n°3
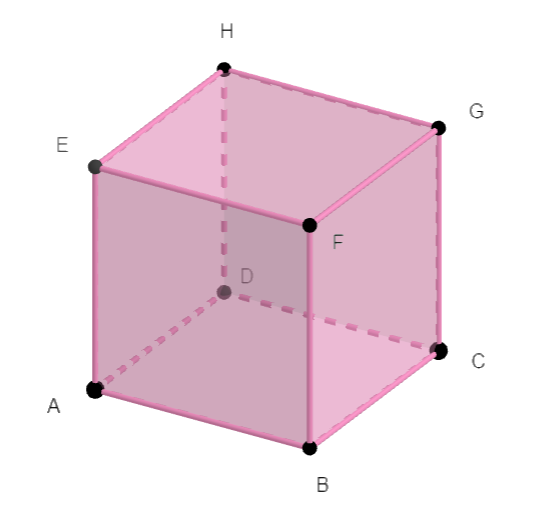
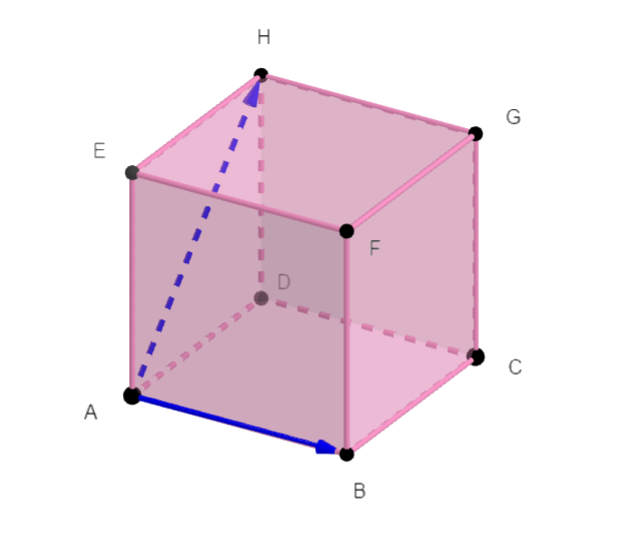
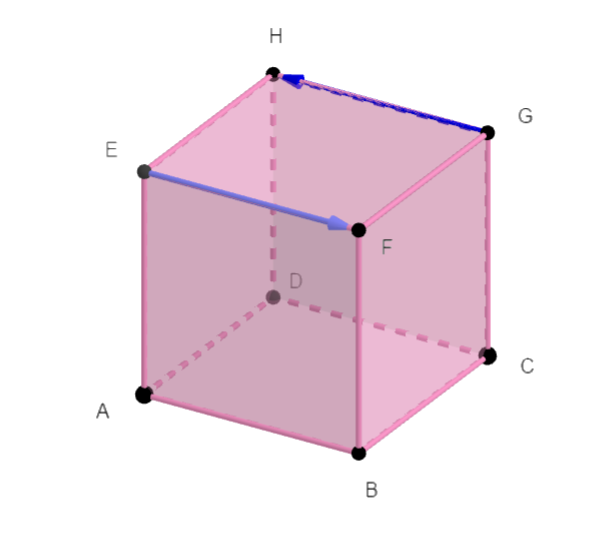
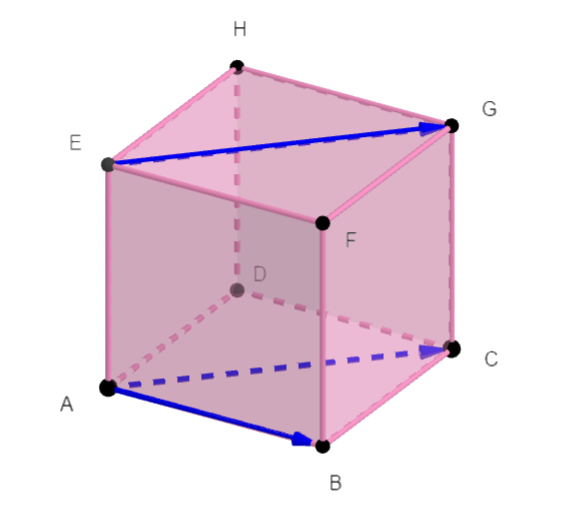
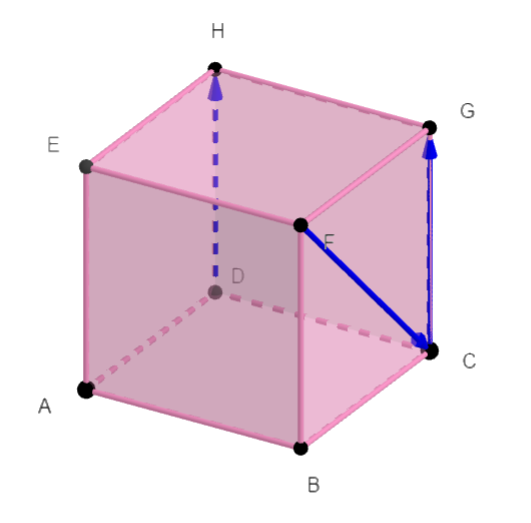
ABCDEFGH est un cube de côté 4.
En utilisant la propriété avec la projection orthogonale, calculer les produits scalaires suivants :
Propriétés algébriques du produit scalaire dans l’espace
Propriété
Pour tous vecteurs \overrightarrow{u} et \overrightarrow{v} , \overrightarrow{u} et \overrightarrow{v} sont orthogonaux équivaut à \overrightarrow{u}.\overrightarrow{v}=0.
Exercice n°4
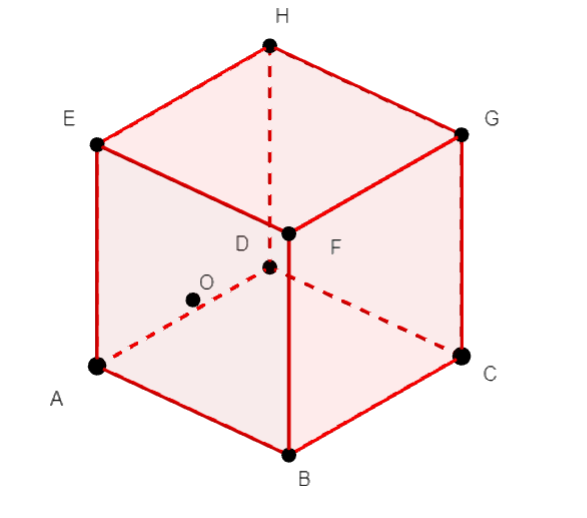
ABCDEFGH est un cube et O est le centre de la face ABFE.
En utilisant la propriété précédente justifier les égalités suivantes :
Propriétés
Pour tous vecteurs \overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w}. Pour tout réel k
\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}
\overrightarrow{u}.(\overrightarrow{v}+\overrightarrow{w})=\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{w}
(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}
\overrightarrow{u}.(\overrightarrow{kv})=k(\overrightarrow{u}.\overrightarrow{v})
(\overrightarrow{ku}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})
Exercice n°5
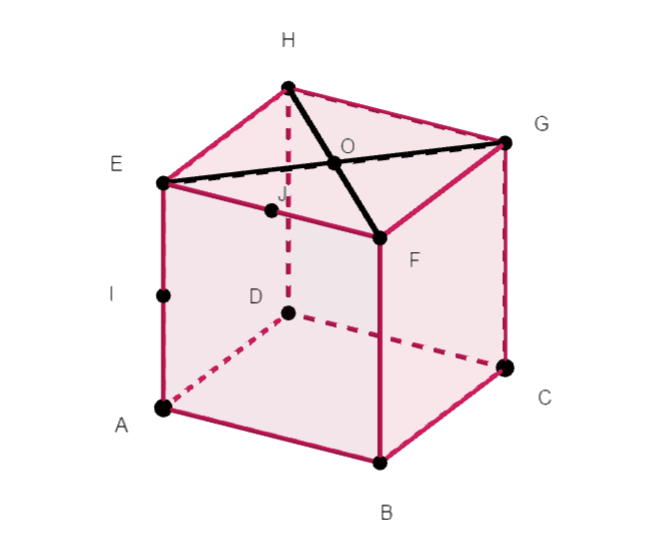
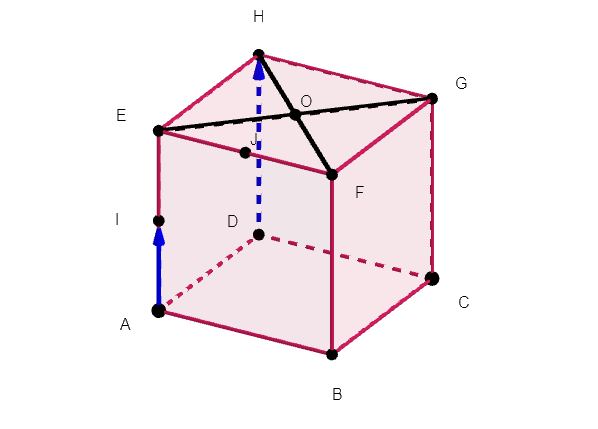
ABCDEFGH est un cube de côté 4 , O est le centre de la face EFGH, I est le milieu de [AE] et J est le milieu de [EF].
- Calculer le produit scalaire \overrightarrow{DH}.\overrightarrow{AI}
2. Calculer le produit scalaire \overrightarrow{HO}.\overrightarrow{BA}
3. Terminer le calcul du produit scalaire \overrightarrow{DO}.\overrightarrow{BI}\\ \overrightarrow{DO}.\overrightarrow{BI}=(\overrightarrow{DH}+\overrightarrow{HO}).(\overrightarrow{BA}+\overrightarrow{AI}).
Exercice n°6
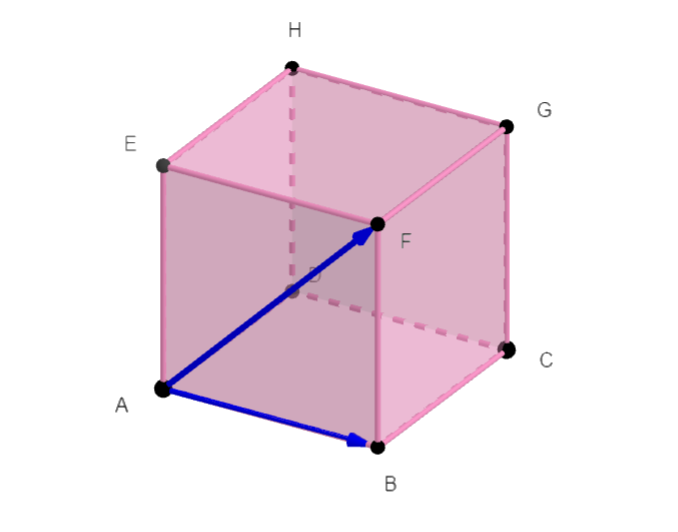
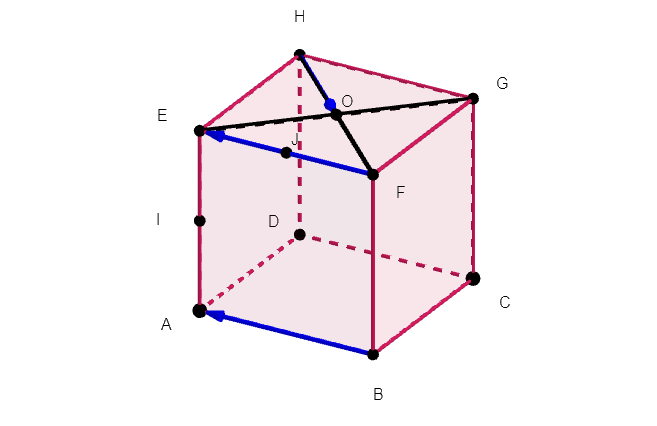
ABCDEFGH est un cube de côté 6, I est défini par \overrightarrow{AI}=\frac{1}{3}\overrightarrow{AE} et J est le milieu de [FG].
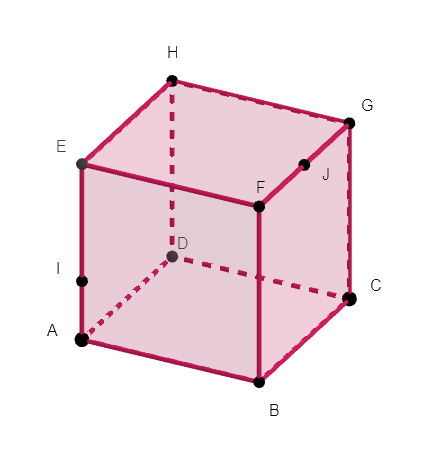
- Calculer les produits scalaires \overrightarrow{BA}.\overrightarrow{BF}, \overrightarrow{BA}.\overrightarrow{FJ} et \overrightarrow{AI}.\overrightarrow{FJ}.
2. Calculer le produit scalaire \overrightarrow{AI}.\overrightarrow{BF}.
3. Terminer le calcul du produit scalaire \overrightarrow{BI}.\overrightarrow{BJ}\\ \overrightarrow{BI}.\overrightarrow{BJ}=(\overrightarrow{BA}+\overrightarrow{AI}).(\overrightarrow{BF}+\overrightarrow{FJ}).
Expression analytique du produit scalaire
Propriété
Soient \overrightarrow{u}(x;y;z) et \overrightarrow{v}(x’;y’;z’) dans une base orthonormée (\overrightarrow{i};\overrightarrow{j};\overrightarrow{k})
\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’
Démonstration
Calculer \overrightarrow{u}.\overrightarrow{v} en remplaçant \overrightarrow{u} par x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k} et \overrightarrow{v} par x’\overrightarrow{i}+y’\overrightarrow{j}+z’\overrightarrow{k}.
Exercice n°7
Calculer le produit scalaire \overrightarrow{u}.\overrightarrow{v} dans chaque cas
\overrightarrow{u}(2;1;1) et \overrightarrow{v}(3;2;2)
\overrightarrow{u}(1;4;6) et \overrightarrow{v}(5;3;-2)
\overrightarrow{u}(\sqrt{2};1;-1) et \overrightarrow{v}(\sqrt{2};3;0)
\overrightarrow{u}(1;0;1) et \overrightarrow{v}(0;1;0)
Propriété
Soient \overrightarrow{u}(x;y;z) et \overrightarrow{v}(x’;y’;z’) dans une base orthonormée (\overrightarrow{i};\overrightarrow{j};\overrightarrow{k})
- \overrightarrow{u} et \overrightarrow{v} sont orthogonaux équivaut à xx’+yy’+zz’=0
- ||\overrightarrow{u}||=\sqrt{x^2+y^2+z^2}
Exercice n°8
Calculer le produit scalaire \overrightarrow{u}.\overrightarrow{v} dans chaque cas et dire si les vecteurs sont orthogonaux ou pas.
\overrightarrow{u}(5;-6;1) et \overrightarrow{v}(3;2;-3)
\overrightarrow{u}(1;0;0) et \overrightarrow{v}(0;3;0)
\overrightarrow{u}(\sqrt{2};-1;-1) et \overrightarrow{v}(\sqrt{2};3;-1)
\overrightarrow{u}(1;6;1) et \overrightarrow{v}(-5;1;0)
Exercice n°9
Soient A(1;1;3) , B(4;5;0) , C(6;1;1) et D(1;4;0).
Démontrer que les droites (AB) et (CD) sont orthogonales.
Exercice n°10
Soient A(1;-1;6) , B(9;-1-1) , C(4;3;-3) et D(6;1;-1).
Démontrer que les droites (AB) et (CD) sont orthogonales.
Exercice n°11
Calculer la norme du vecteur \overrightarrow{u} dans chaque cas.
Propriété
Soient A(x_A;y_A;z_A) et B(x_B;y_B;z_B) dans un repère orthonormé (O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k})
AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}.
Exercice n°12 :
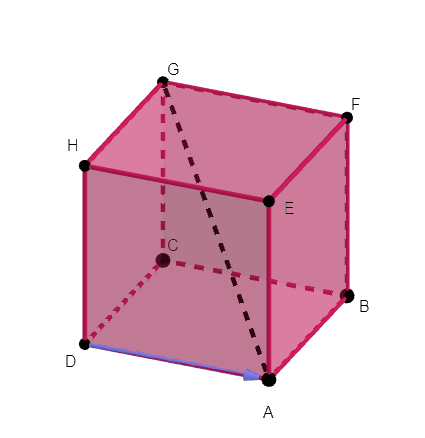
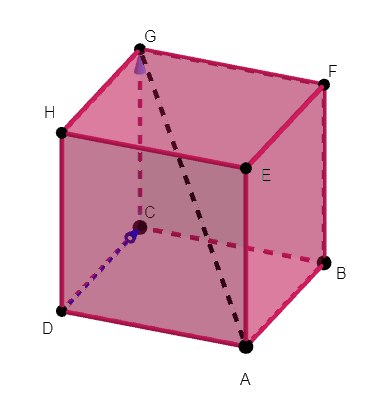
ABCDEFGH est un cube de côté 1.
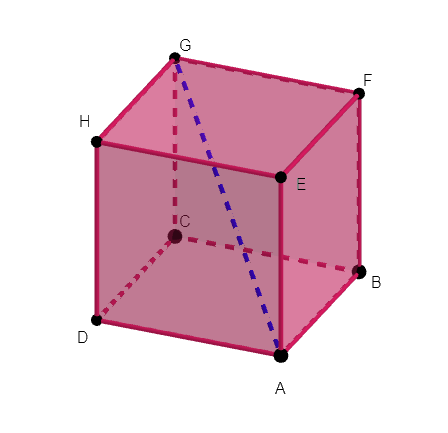
1.Déterminer graphiquement les coordonnées des points A et G dans le repère orthonormé (D;\overrightarrow{DA};\overrightarrow{DC};\overrightarrow{DH})
2. En utilisant la propriété précédente, calculer la distance AG.