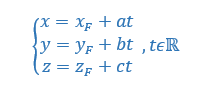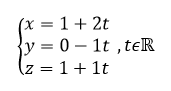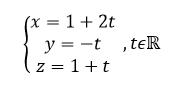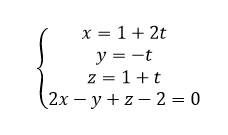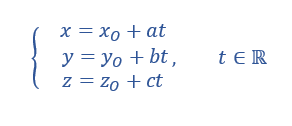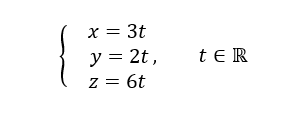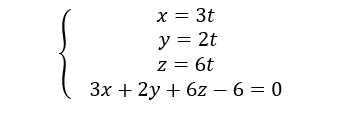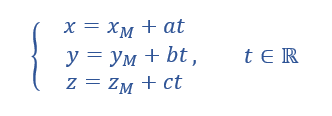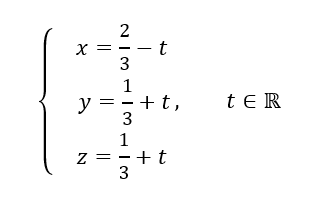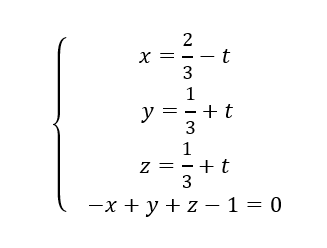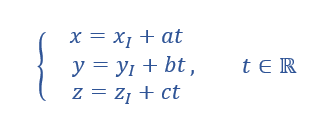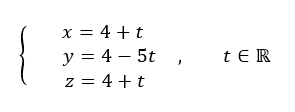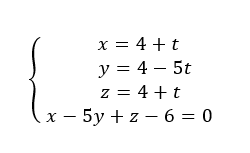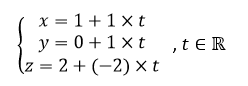logo

T. Géométrie dans l’espace. Exercices type bac 2021

Sommaire

Exercice n°1 ( sujet 0 session 2021 )

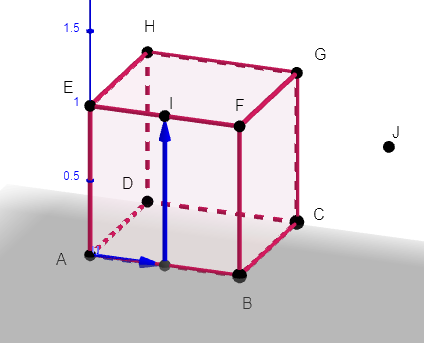
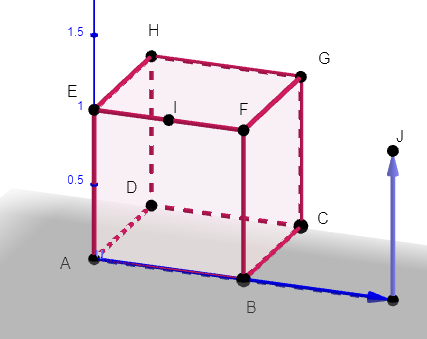
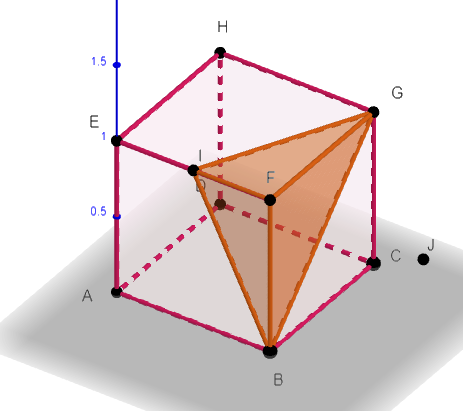
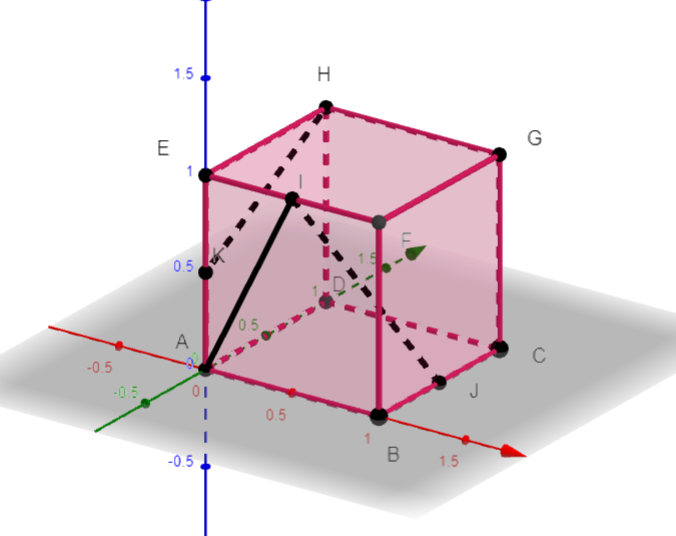
On considère le cube ABCDEFGH de côté 1, le milieu I de [EF] et et J le symétrique de E par rapport à F.

Dans tout l’exercice, l’espace est rapporté au repère orthonormé (A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}).

1. a. Par lecture graphique, donner les coordonnées des points I et J.

Pour afficher les coordonnées du point J, par exemple, cliquer droit sur le point J de la fenêtre active Géogébra ci-dessus. Apparaît alors Point  J(2;0;1).

correction point I
correction point J

b. En déduire les coordonnées des vecteurs \overrightarrow{DJ} , \overrightarrow{BI} et \overrightarrow{BG}.

Pour conjecturer les coordonnées du vecteur \overrightarrow{DJ}, par exemple, à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point D puis sur le point J. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées du vecteur \overrightarrow{DJ}.

correction \overrightarrow{DJ}
correction \overrightarrow{BI}
correction \overrightarrow{BG}

c. Montrer que \overrightarrow{DJ} est un vecteur normal au plan (BGI).

correction

d. Déterminer une équation cartésienne du plan (BGI).

Pour conjecturer une équation cartésienne du plan (BGI) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point B puis sur le point G et sur le point I . Dans la colonne Algèbre située à gauche, apparaît l’équation cartésienne du plan   (BGI) :x-0.5y+0.5z=1 .

correction

2. On note d la droite passant par F et orthogonale au plan (BGI).
a. Déterminer une représentation paramétrique de la droite d.

Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point F puis sur le plan (BGI) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(1,0,1)+\lambda (1,-0.5,0.5).

correction

b.  L est le point d’intersection de la droite d et du plan (BGI). Déterminer les coordonnées de L  par le calcul.

Pour conjecturer les coordonnées du point L à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le plan (BGI) . Dans la colonne Algèbre située à gauche, apparaît  K=intersection(f,p)   :  (0.67,0.17,0.83).

Remarque : on peut renommer K en L.

utiliser la TI 83 CE pour résoudre un système
correction

3. On rappelle que le volume V d’une pyramide est donné par la formule
V=\frac{1}{3}\times B\times h
où B  est l’aire d’une base et h la hauteur associée à cette base.

a. Calculer le volume de la pyramide FBGI.

Pour conjecturer le volume de la pyramide FBGI à l’aide de la fenêtre active géogébra ci-dessus. Saisir dans la colonne Algèbre  Pyramide(I,F,G,B), apparaît alors en dessous le nombre 0.08 qui est son volume.

correction

b. En déduire l’aire du triangle BGI.

Pour conjecturer l’aire du triangle BGI à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le cinquième onglet en haut à partir de la gauche et sélectionner Polygone dans le menu déroulant. Dans le repère cliquer sur le point B puis sur le point G et sur le point I . Dans la colonne Algèbre située à gauche, apparaît l’aire du triangle BGI  :  0.61 .

correction

Exercice n°2 ( 15 mars 2021 sujet 2 )

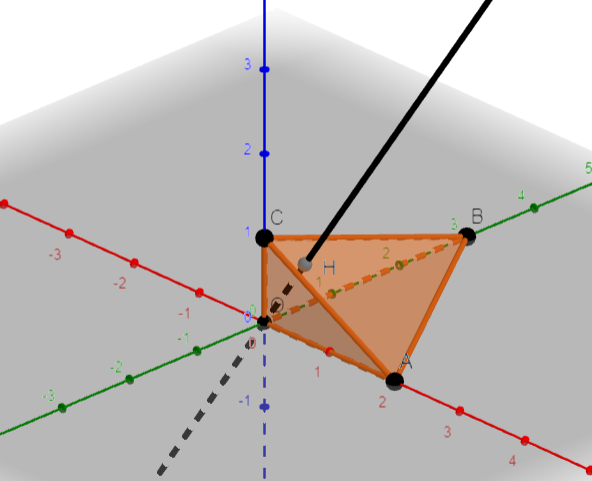
Dans l’espace rapporté au repère orthonormé (O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}), on considère les pointsA(2;0;0),B(0;3;0) et C(0;0;1).

L’objectif de cet exercice est de calculer l’aire du triangle ABC.

Pour conjecturer l’aire du triangle ABC à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le cinquième onglet en haut à partir de la gauche et sélectionner Polygone dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B et sur le point C . Dans la colonne Algèbre située à gauche, apparaît l’aire du triangle ABC  :  3.5 .

1. a. Montrer que le vecteur \overrightarrow{n}(3;2;6) est normal au plan (ABC).

correction

b. En déduire qu’une équation cartésienne du plan (ABC) est : 3x+2y+6z-6=0.

Pour conjecturer une équation cartésienne du plan (ABC) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B et sur le point C . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   (ABC) :-3x-2y-6z=-6 .

correction

2. On note d la droite passant par 0 et orthogonale au plan (ABC).
a. Déterminer une représentation paramétrique de la droite d.

Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point O puis sur le plan (ABC) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(0,0,0)+\lambda (-3,-2,-6).

correction

b. Montrer que la droite d coupe le plan (ABC) au point H de coordonnées (\frac{18}{49}; \frac{12}{49};\frac{36}{49} ).

Pour conjecturer les coordonnées du point H à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le plan (ABC) . Dans la colonne Algèbre située à gauche, apparaît  E=intersection(f,p)   :  (0.37,0.24,0.73).

Remarque : on peut renommer E en H.

utiliser la TI 83 CE pour résoudre un système
correction

c. Calculer la distance OH.

Pour conjecturer la distance  OH à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le onzième onglet en haut à partir de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer sur le point 0 puis sur le point H. Dans la colonne Algèbre située à gauche, apparaît la distance 0.86.

correction

3. On rappelle que le volume V d’une pyramide est donné par la formule
V=\frac{1}{3}\times B\times h
où B  est l’aire d’une base et h la hauteur associée à cette base.
En calculant de deux façons différentes le volume de la pyramide OABC, déterminer l’aire
du triangle ABC.

Pour conjecturer le volume de la pyramide OABC à l’aide de la fenêtre active géogébra ci-dessus. Saisir dans la colonne Algèbre  Pyramide(O,A,B,C), apparaît alors en dessous le nombre 1 qui est son volume.

correction

Exercice n°3 ( Amérique du nord session 2021 )

On considère le cube ABCDEFGH de côté 1. Le point I est le milieu du segment [EF], le point J est le milieu du segment [BC] et le point K est le milieu du segment [AE].

1. Les droites (AI) et (KH) sont-elles parallèles ? Justifier votre réponse.

correction

Dans la suite, on se place dans le repère orthonormé (A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE})
2. a. Donner les coordonnées des points A, B, C, D, E, F et G.

Pour afficher les coordonnées du point H, par exemple, cliquer droit sur le point H de la fenêtre active Géogébra ci-dessus. Apparaît alors Point  H(0;1;1).

correction

2. b. Calculer les coordonnées des points Iet J.

Lors de leurs constructions respectives dans la fenêtre Géogébra ci-dessus, leurs coordonnées sont apparues dans la colonne Algèbre située à gauche. 

correction point I
correction point J

2. c. Montrer que les vecteurs \overrightarrow{IJ}, \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires.

Lors de leurs constructions respectives dans la fenêtre Géogébra ci-dessus, leurs coordonnées sont apparues dans la colonne Algèbre située à gauche. 

correction

On considère le plan P d’équation  x+3y-2z=0 ainsi que les droites d_1 et d_2.

représentation paramétrique de d_1

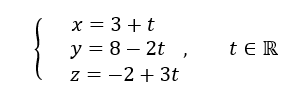
représentation paramétrique de d_2

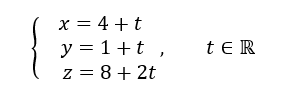
3. Les droites d_1 et d_2 sont-elles parallèles ? Justifier votre réponse. 

correction

4. Montrer que la droite d_2 est parallèle au plan P .

correction

5. Montrer que le point L(4;0;3)est le projeté orthogonal du point M(5;3;1) sur le plan P.

correction

Exercice n°4 ( Polynésie session 2021 )

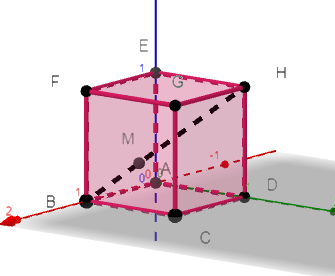
Dans l’espace, on considère le cube ABCDEFGH de côté 1. Le point M est défini par \overrightarrow{BM}=\frac{1}{3}\overrightarrow{BH}.

Dans tout l’exercice, l’espace est rapporté au repère orthonormé (A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}).

1. Par lecture graphique, donner les coordonnées des points A, B, C, D, E, F et G.

Pour afficher les coordonnées du point E, par exemple, cliquer droit sur le point E de la fenêtre active Géogébra ci-dessus. Apparaît alors Point  E(0;0;1).

correction

2. a. Quelle est la nature du triangle EGD ? Justifier la réponse.

correction

2. b. On admet que l’aire d’un triangle équilatéral de côté c est égale à \frac{\sqrt{3}}{4}c^2.
Montrer que l’aire du triangle EGD est égale à \frac{\sqrt{3}}{2}.

correction

3. Démontrer que les coordonnées de M sont (\frac{2}{3};\frac{1}{3};\frac{1}{3}).

Lors de la construction du point M, ses coordonnées sont apparues dans la colonne Algèbre située à gauche de l’écran  M=(0.67,0.33,0.33).

correction

4. a. Justifier que le vecteur \overrightarrow{n}(-1;1;1) est normal au plan (EGD).

correction

b. En déduire qu’une équation cartésienne du plan (EGD) est : -x+y+z-1=0.

Pour conjecturer une équation cartésienne du plan (EGD) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point E puis sur le point G et sur le point D . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   (EGD) :-x+y+z=1 .

correction

c. Soit  \Delta la droite orthogonale au plan (EGD) et passant par le point M.
Montrer qu’une représentation paramétrique de cette droite est :

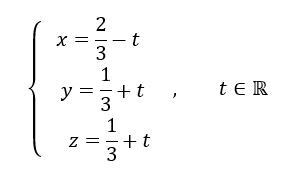
Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point M puis sur le plan (EGD) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(0.67,0.33,0.33)+\lambda (-1,1,1).

correction

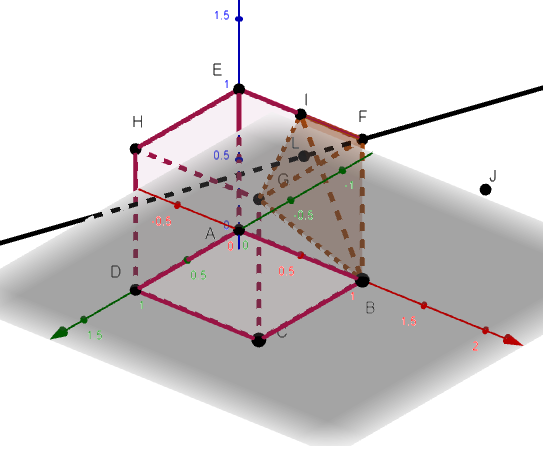
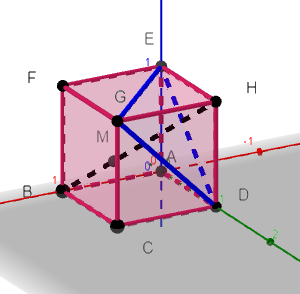
5. Le cube ABCDEFGH est représenté ci-dessus selon une vue qui permet de mieux percevoir la pyramide GEDM , en bleu sur la figure :

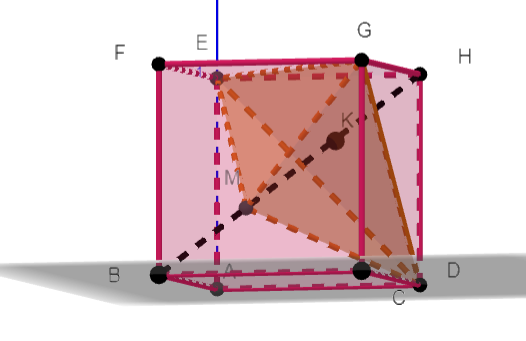
Le but de cette question est de calculer le volume de la pyramide GEDM.

Pour conjecturer le volume de la pyramide GEDM à l’aide de la fenêtre active géogébra ci-dessus. Saisir dans la colonne Algèbre  Pyramide(G,E,D,M), apparaît alors en dessous le nombre 0.17 qui est son volume.

a. Soit K, le pied de la hauteur de la pyramide GEDM issue du point M.
Démontrer que les coordonnées du point K sont (\frac{1}{3};\frac{2}{3};\frac{2}{3})

Pour conjecturer les coordonnées du point K à l’aide de la fenêtre active géogébra ci-dessus.

-Construire le plan (GED)

-Construire la droite perpendiculaire au plan (GED) passant par M

-Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  et le plan qu’on vient de construire . Dans la colonne Algèbre située à gauche, apparaît  I=intersection(f,p)   :  (0.33,0.66,0.66).

Remarque : on peut renommer I en K.

correction

b. En déduire le volume de la pyramide GEDM.
On rappelle que le volume V d’une pyramide est donné par la formule
V=\frac{1}{3}\times B\times h
où B désigne l’aire d’une base et h la hauteur associée.

correction

Exercice n°5 ( Asie 7 juin 2021 )

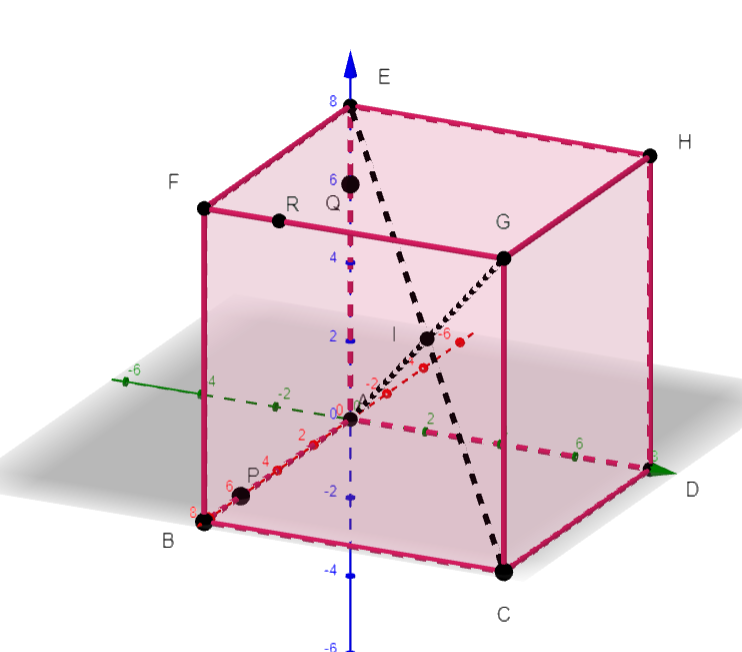
Dans l’espace, on considère le cube ABCDEFGH de côté 8 et de centre I.

P est défini par \overrightarrow{AP}=\frac{3}{4}\overrightarrow{AB} , Q est défini par \overrightarrow{AQ}=\frac{3}{4}\overrightarrow{AE} et  R est défini par \overrightarrow{FR}=\frac{1}{4}\overrightarrow{FG}.

L’espace est rapporté au repère orthonormé (A;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}) où  \overrightarrow{i}=\frac{1}{8}\overrightarrow{AB},  \overrightarrow{j}=\frac{1}{8}\overrightarrow{AD} et  \overrightarrow{k}=\frac{1}{8}\overrightarrow{AE}

Partie I
1. Dans ce repère, on admet que les coordonnées du point R sont (8;2;8).
Lire graphiquement les coordonnées des points P et Q.

Lors de la construction du point R, ses coordonnées sont apparues dans la colonne Algèbre située à gauche de l’écran  R=(8,2,8).Idem pour les points P et Q.

correction

2. Montrer que le vecteur \overrightarrow{n}(1;-5,1) est un vecteur normal au plan (PQR).

correction

3. Justifier qu’une équation cartésienne du plan (PQR) est x-5y+z-6=0.

Pour conjecturer une équation cartésienne du plan (PQR) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point P puis sur le point Q et sur le point R . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   (PQR) :x-5y+z=6.

correction

Partie II
On note L le projeté orthogonal du point I sur le plan (PQR).
1. Justifier que les coordonnées du point I sont (4;4;4).

Lors de la construction du point I, ses coordonnées sont apparues dans la colonne Algèbre située à gauche de l’écran  I=(4,4,4).

correction

2. Donner une représentation paramétrique de la droite d perpendiculaire au plan (PQR)
et passant par I.

Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point I puis sur le plan (PQR) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(4,4,4)+\lambda (12,-60,12).

correction

3. Montrer que les coordonnées du point L sont (\frac{14}{3};\frac{2}{3};\frac{14}{3})

Pour conjecturer les coordonnées du point L à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le plan (PQR) . Dans la colonne Algèbre située à gauche, apparaît  J=intersection(f,p)   :  (4.67,0.67,4.67).

Remarque : on peut renommer J en L.

correction

4. Calculer la distance du point I au plan (PQR).

Pour conjecturer la distance  IL à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le onzième onglet en haut à partir de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer sur le point 0 puis sur le point H. Dans la colonne Algèbre située à gauche, apparaît la distance 3.46.

correction

Exercice n°6 ( Métropole 13 Septembre 2021 J2 )

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n’est demandée.

Dans l’espace rapporté à un repère orthonormé (O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}), on considère le point A(1;0;2), le point B(2;1;0) et le point le point C(0;1;2). On considère la droite  d de représentation paramétrique 

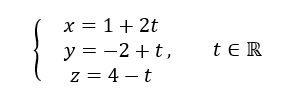
1. Parmi les points suivants, lequel appartient à la droite  d?

a. M(2;1;-1)

b. N(-3;-4;6)

c. P(-3;-4;2)

d. Q(-5;-5;1)

Pour placer le point M dans le repère à l’aide de la fenêtre active géogébra ci-dessus, saisir M=(2,1,-1) dans la colonne Algèbre située à gauche. Puis regarder si le point est sur la droite d.

correction

2. Le vecteur \overrightarrow{AB} admet pour coordonnées.

a. (1.5;0.5;1)

b. (-1;-1;2)

c. (1;1;-2)

d. (3;1;2)

Pour conjecturer les coordonnées de \overrightarrow{AB}à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées  (1,1,-2).

correction

3. Une représentation paramétrique de la droite  (AB) est:

Réponse a

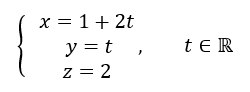
Réponse b

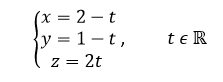
Réponse c

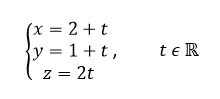
Réponse d

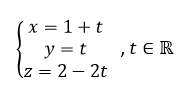
Pour conjecturer une représentation paramétrique de la droite (AB) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite (AB)  :  X=(2,1,0)+\lambda (-1,-1,2).

correction

4. Une équation cartésienne du plan passant par le point C et orthogonal à la droite d
est :

a. x −2y +4z −6 = 0

b. 2x + y − z +1 = 0

c.  2x + y − z −1 = 0

d. y +2z −5 = 0

Pour conjecturer une équation cartésienne du plan passant par C et orthogonal à la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan perpendiculaire dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le point C . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   2x+y-z=-1.

correction

©2020 – Math’O karé SAS

Pour déterminer les coordonnées du point I, il faut :

Partir de l’origine  A  pour se rendre au point I  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  \frac{1}{2}\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc I(\frac{1}{2};0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point J, il faut :

Partir de l’origine  A  pour se rendre au point J  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  2\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc J(2;0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

On calcule les coordonnées du vecteur \overrightarrow{DJ}.

Je repère les coordonnées des points D et J.

\hspace{0.2cm}x_{D}\hspace{0.05cm}y_{D}\hspace{0.05cm}z_{D}\hspace{2.1cm}x_{J}\hspace{0.05cm}y_{J}\hspace{0.05cm}z_{J}

D(0;1;0)\hspace{2cm}J(2;0;1)

J’écris la formule :

\overrightarrow{DJ}(x_{J}-x_{D};y_{I}-y_{D};z_{I}-z_{D})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{DJ}(2-0;0-1;1-0)

\overrightarrow{DJ}(2;-1;1)

 

On calcule les coordonnées du vecteur \overrightarrow{BI}.

Je repère les coordonnées des points B et I.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{I}\hspace{0.05cm}y_{I}\hspace{0.05cm}z_{I}

B(1;0;0)\hspace{2cm}I(\frac{1}{2};0;1)

J’écris la formule :

\overrightarrow{BI}(x_{I}-x_{B};y_{I}-y_{B};z_{I}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BI}(\frac{1}{2}-1;0-0;1-0)

\overrightarrow{BI}(-\frac{1}{2};0;1)

On calcule les coordonnées du vecteur \overrightarrow{BG}.

Je repère les coordonnées des points B et G.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{G}\hspace{0.05cm}y_{G}\hspace{0.05cm}z_{G}

B(1;0;0)\hspace{2cm}G(1;1;1)

J’écris la formule :

\overrightarrow{BG}(x_{G}-x_{B};y_{G}-y_{B};z_{G}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BG}(1-1;1-0;1-0)

\overrightarrow{BG}(0;1;1)

On remarque que \overrightarrow{BI}(-\frac{1}{2};0;1)et \overrightarrow{BG}(0;1;1) ne sont pas colinéaires car leurs coordonnées ne sont pas proportionnelles.

On calcule le produit scalaire  \overrightarrow{DJ}.\overrightarrow{BI}.

\overrightarrow{DJ}(2;-1;1).

\overrightarrow{BI}(-\frac{1}{2};0;1).

Pour calculer  \overrightarrow{DJ}.\overrightarrow{BI}, on remplace : 

 x par 2 ,  y par (-1) ,  z par 1.

 x’ par (-\frac{1}{2}) ,  y’ par 0 ,  z’ par 1, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{DJ}.\overrightarrow{BI}=2\times (-\frac{1}{2})+(-1)\times 0+1\times 1\\\overrightarrow{DJ}.\overrightarrow{BI}=-1+0+1\\\overrightarrow{DJ}.\overrightarrow{BI}=0

Donc les vecteurs  \overrightarrow{DJ} et  \overrightarrow{BI} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{DJ}.\overrightarrow{BG}.

\overrightarrow{DJ}(2;-1;1).

\overrightarrow{BG}(0;1;1).

Pour calculer  \overrightarrow{DJ}.\overrightarrow{BG}, on remplace : 

 x par 2 ,  y par (-1) ,  z par 1.

 x’ par 0 ,  y’ par 1 ,  z’ par 1, dans:

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{DJ}.\overrightarrow{BG}=2\times 0+(-1)\times 1+1\times 1\\\overrightarrow{DJ}.\overrightarrow{BG}=0-1+1\\\overrightarrow{DJ}.\overrightarrow{BG}=0

Donc les vecteurs  \overrightarrow{DJ} et  \overrightarrow{BG} sont orthogonaux.

Le vecteur   \overrightarrow{DJ} est orthogonal à   \overrightarrow{BI} et \overrightarrow{BG}, donc il est normal au plan (BGI)

On veut déterminer une équation cartésienne du plan  (BGI) de vecteur normal \overrightarrow{DJ}.

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{DJ} a pour coordonnées (2;-1;1).

On remplace a par 2 et b par -1 et c par 1 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (BGI) est de la forme :

2x-y+z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(BGI) passe par B(1;0;0), on remplace x par 1,  y par 0 et z par 0 dans 2x-y+z+d=0.

2\times 1-0+0+d=0

2+d=0

d=-2

Une équation cartésienne du plan  (BGI) est 2x-y+z-2=0

d est la droite passant par F et orthogonale au plan (BGI).
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (BGI), alors le vecteur normal au plan  \overrightarrow{n}(2;-1;1) est un vecteur directeur de la droite d.

De plus la droite d passe par le point F(1;0;1).

On remplace x_F par 1, y_F par 0, z_F par 1 ,a par 2, b par -1 et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

Remarque : la représentation donnée par géogébra est exacte aussi car les vecteurs de coordonnées (2;-1;1) et (1;-0.5;0.5) sont colinéaires.

 

L est le point d’intersection de la droite d et du plan (BGI). 

L\in d donc ses coordonnées vérifient le système 

L\in (BGI) donc ses coordonnées vérifient l’équation 2x-y+z-2=0 

Comme L est le point d’intersection de la droite d et du plan (BGI). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

2(1+2t)-(-t)+(1+t)-2=0\\2+4t+t+1+t-2=0\\6t+1=0\\6t=-1\\t=-\frac{1}{6}

Pour trouver les valeurs de x,y,z, on remplace t par -\frac{1}{6} dans les 3 premières équations.

x=1+2\times(-\frac{1}{6})\\x=1-\frac{1}{3}\\x=\frac{2}{3}
y=-(-\frac{1}{6})\\y=\frac{1}{6}

 

z=1+(-\frac{1}{6})\\x=1-\frac{1}{6}\\x=\frac{5}{6}

Donc L a pour coordonnées (\frac{2}{3};\frac{1}{6};\frac{5}{6}).

 

 

Pour déterminer le volume de la pyramide FBGI, il faut choisir une base. Ici on choisit le triangle rectangle isocèle FBG. La hauteur correspondante sera  [IF].

L’aire du triangle FBG est la moitié du carré FBCG de côté 1, elle vaut \frac{1}{2}.

IF=\frac{EF}{2}=\frac{1}{2}

Pour calculer le volume de la pyramide, on remplace B par \frac{1}{2} et h par \frac{1}{2} dans la formule B par V=\frac{B\times h}{3}

V=\frac{\frac{1}{2}\times \frac{1}{2}}{3}

V=\frac{\frac{1}{4}}{3}

V=\frac{1}{12}

 

 

Le volume de la pyramide FBGI ne change pas si on change la base. Ici on choisit le triangle  BGI. La hauteur correspondante sera  [FL].

V=\frac{aire(BGI)\times FL}{3}

\frac{aire(BGI)\times FL}{3}=\frac{1}{12}

On calcule la distance FL.

F(1;0;1)\\L(\frac{2}{3};\frac{1}{6};\frac{5}{6})

Pour calculer la distance FL de la pyramide, on remplace x_L par \frac{2}{3} , y_L par \frac{1}{6} , z_L par \frac{5}{6} , x_F par 1 , y_F par 0 et z_F par 1dans la formule

FL=\sqrt{(x_L-x_F)^2+(y_L-y_F)^2+(z_L-z_F)^2}

FL=\sqrt{(\frac{2}{3}-1)^2+(\frac{1}{6}-0)^2+(\frac{5}{6}-1)^2}

On effectue ce qu’il y a entre parenthèses 

FL=\sqrt{(\frac{2}{3}-\frac{3}{3})^2+(\frac{1}{6})^2+(\frac{5}{6}-\frac{6}{6})^2}\\FL=\sqrt{(-\frac{1}{3})^2+(\frac{1}{6})^2+(-\frac{1}{6})^2}

On effectue les puissances

FL=\sqrt{\frac{1}{9}+\frac{1}{36}+\frac{1}{36}}

On ajoute en mettant au même dénominateur

FL=\sqrt{\frac{1}{9}\times \frac{4}{4}+\frac{1}{36}+\frac{1}{36}}\\FL=\sqrt{\frac{4}{36}+\frac{1}{36}+\frac{1}{36}}\\FL=\sqrt{\frac{6}{36}}\\FL=\sqrt{\frac{1}{6}}

Pour déterminer l’aire de BGI , on remplace FL par \sqrt{\frac{1}{6}} dans  \frac{aire(BGI)\times FL}{3}=\frac{1}{12}

\frac{aire(BGI)\times \sqrt{\frac{1}{6}}}{3}=\frac{1}{12}\\aire(BGI)\times \sqrt{\frac{1}{6}}=3\times \frac{1}{12}\\aire(BGI)\times \sqrt{\frac{1}{6}}=\frac{1}{4}\\aire(BGI)=\frac{\frac{1}{4}}{\sqrt{\frac{1}{6}}}\\aire(BGI)=\frac{1}{4}\times{\sqrt{6}}\\aire(BGI)=\frac{\sqrt{6}}{4}

 

Pour montrer que le vecteur  \overrightarrow{n} est normal au plan (ABC), on va montrer qu’il est orthogonal aux vecteurs non colinéaires  \overrightarrow{AB} et \overrightarrow{AC}.

On commence par calculer les coordonnées des vecteurs \overrightarrow{AB} et \overrightarrow{AC}.

On calcule les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(2;0;0)\hspace{2cm}B(0;3;0)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(0-2;3-0;0-0)

\overrightarrow{AB}(-2;3;0)

On calcule les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{C}\hspace{0.05cm}y_{C}\hspace{0.05cm}z_{C}

A(2;0;0)\hspace{2cm}C(0;0;1)

J’écris la formule :

\overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A};z_{C}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(0-2;0-0;1-0)

\overrightarrow{AC}(-2;0;1)

Ensuite on calcule les produit scalaires  \overrightarrow{n}.\overrightarrow{AB} et \overrightarrow{n}.\overrightarrow{AC}.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{AB}.

\overrightarrow{n}(3;2;6).

\overrightarrow{AB}(-2;3;0).

Pour calculer  \overrightarrow{n}.\overrightarrow{AB}, on remplace : 

 x par 3 ,  y par 2 ,  z par 6.

 x’ par (-2) ,  y’ par 3 ,  z’ par 0, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{AB}=3\times (-2)+2\times 3+6\times 0\\\overrightarrow{n}.\overrightarrow{AB}=-6+6+0\\\overrightarrow{n}.\overrightarrow{AB}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{AB} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{AC}.

\overrightarrow{n}(3;2;6).

\overrightarrow{AC}(-2;0;1).

Pour calculer  \overrightarrow{n}.\overrightarrow{AC}, on remplace : 

 x par 3 ,  y par 2 ,  z par 6.

 x’ par (-2) ,  y’ par 0 ,  z’ par 1, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{AC}=3\times (-2)+2\times 0+6\times 1\\\overrightarrow{n}.\overrightarrow{AC}=-6+0+6\\\overrightarrow{n}.\overrightarrow{AC}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{AC} sont orthogonaux.

Le vecteur   \overrightarrow{n} est orthogonal à   \overrightarrow{AB} et \overrightarrow{AC}, donc il est normal au plan (ABC)

 

 

On veut déterminer une équation cartésienne du plan  (ABC) de vecteur normal \overrightarrow{n}.

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{n} a pour coordonnées (3;2;6).

On remplace a par 3 et b par 2 et c par 6 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (ABC) est de la forme :

3x+2y+6z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(ABC) passe par A(2;0;0), on remplace x par 2,  y par 0 et z par 0 dans 3x+2y+6z+d=0.

3\times 2+2\times 0+6\times 0+d=0

6+d=0

d=-6

Une équation cartésienne du plan  (ABC) est 3x+2y+6z-6=0

d est la droite passant par O et orthogonale au plan (ABC).
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (ABC) , alors le vecteur normal au plan  \overrightarrow{n}(3;2;6) est un vecteur directeur de la droite d.

De plus la droite d passe par le point O(0;0;0).

On remplace x_O par 0, y_O par 0, z_O par 0, a par 3,  b par 2 et c par 6 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

Remarque : la représentation donnée par géogébra est exacte aussi car les vecteurs de coordonnées (3;2;6) et (-3;-2;-6) sont colinéaires.

H est le point d’intersection de la droite d et du plan (ABC). 

H\in d donc ses coordonnées vérifient le système 

H\in (ABC) donc ses coordonnées vérifient l’équation 3x+2y+6z-6=0 

Comme H est le point d’intersection de la droite d et du plan (ABC). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

3(3t)+2(2t)+6(6t)-6=0\\9t+4t+36t-6=0\\49t-6=0\\49t=6\\t=\frac{6}{49}

Pour trouver les valeurs de x,y,z, on remplace t par \frac{6}{49} dans les 3 premières équations.

x=3\times\frac{6}{49}\\x=\frac{18}{49}
y=2\times\frac{6}{49}\\x=\frac{12}{49}
z=6\times\frac{6}{49}\\x=\frac{36}{49}

Donc H a pour coordonnées (\frac{18}{49};\frac{12}{49};\frac{36}{49}).

 

 

On calcule la distance OH.

O(0;0;0)\\H(\frac{18}{49};\frac{12}{49};\frac{36}{49})

Pour calculer la distance OH, on remplace x_H par \frac{18}{49} , y_H par \frac{12}{49} , z_H par \frac{36}{49} , x_O par 0 , y_O par 0 et z_O par 0dans la formule

OH=\sqrt{(x_H-x_O)^2+(y_H-y_O)^2+(z_H-z_O)^2}

OH=\sqrt{(\frac{18}{49}-0)^2+(\frac{12}{49}-0)^2+(\frac{36}{49}-0)^2}

On effectue ce qu’il y a entre parenthèses 

OH=\sqrt{(\frac{18}{49})^2+(\frac{12}{49})^2+(\frac{36}{49})^2}

On effectue les puissances

OH=\sqrt{\frac{324}{2401}+\frac{144}{2041}+\frac{1296}{2041}}

On ajoute 

OH=\sqrt{\frac{1764}{2401}}\\OH=\frac{\sqrt{1764}}{\sqrt{2401}}\\OH=\frac{42}{49}

On simplifie par 7.

OH=\frac{6}{7}

 

 

Le volume de la pyramide FBGI ne change pas si on change la base.

On choisit pour base le triangle OAB. La hauteur correspondante sera  [OC].

V=\frac{aire(OAB)\times OC}{3}

V=\frac{(\frac{OA\times OB}{2})\times 1}{3}

V=\frac{(\frac{2\times 3}{2})\times 1}{3}

V=\frac{3\times 1}{3}

V=1

On choisit pour base le triangle ABC. La hauteur correspondante sera  [OH].

V=\frac{aire(ABC)\times OH}{3}

V=\frac{aire(ABC)\times \frac{6}{7}}{3}

V=aire(ABC)\times \frac{6}{7}\times \frac{1}{3}

V=aire(ABC)\times \frac{2}{7}

 

On en déduit que aire(ABC)\times \frac{2}{7}=1

Donc :

aire(ABC)=\frac{1}{\frac{2}{7}}

Diviser par un nombre revient à multiplier par son inverse :

aire(ABC)=1\times {\frac{7}{2}}

aire(ABC)=\frac{7}{2}

 

On va utiliser une démonstration par l’absurde.

On va supposer que les droites (AI) et (KH) sont parallèles.

On va montrer que c’est impossible, ce qu’on avait supposé étant faux, c’est le contraire qui est vrai c’est-à-dire que les droites (AI) et (KH) sont parallèles.

On suppose que les droites (AI) et (KH) sont parallèles.

Comme les points A;E;H sont coplanaires, I est aussi dans le plan (AEH) ce qui est impossible.

Donc les droites (AI) et (KH) ne sont pas parallèles.

Pour déterminer les coordonnées d’un point , il faut :

Partir de l’origine  A  pour se rendre au point  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

A est l’origine du repère donc A(0;0;0)

On part de  A, pour aller à B on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc B(1;0;0)

On part de  A, pour aller à C on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc C(1;1;0)

On part de  A, pour aller à D on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc D(0;1;0)

On part de  A, pour aller à E on se déplace de  0\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc E(0;0;1)

On part de  A, pour aller à F on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc F(1;0;1)

On part de  A, pour aller à G on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc G(1;1;1)

On part de  A, pour aller à H on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc H(0;1;1)

 

 

E(0;0;1) et F(1;0;1)

Pour déterminer les coordonnées du point I milieu de [EF] : on remplace x_E par 0, y_E par 0 z_E par 1, x_F par 1, y_F par 0 z_F par 1.  dans :

 x_I=\frac{x_E+x_F}{2} ;  y_I=\frac{y_E+y_F}{2} et  z_I=\frac{z_E+z_F}{2}

 x_I=\frac{0+1}{2} ;  y_I=\frac{0+0}{2} et  z_I=\frac{1+1}{2}

 x_I=\frac{1}{2} ;  y_I=0 et  z_I=1

Donc  I(\frac{1}{2};0;1)

B(1;0;0) et C(1;1;0)

Pour déterminer les coordonnées du point J milieu de [BC] : on remplace x_B par 1, y_B par 0 z_B par 0, x_C par 1, y_C par 1 z_C par 0.  dans :

 x_J=\frac{x_B+x_C}{2} ;  y_J=\frac{y_B+y_C}{2} et  z_J=\frac{z_B+z_C}{2}

 x_J=\frac{1+1}{2} ;  y_J=\frac{0+1}{2} et  z_J=\frac{0+0}{2}

 x_J=1 ;  y_J=\frac{1}{2} et  z_J=0

Donc  J(1;\frac{1}{2};0)

On calcule les coordonnées du vecteur \overrightarrow{IJ}.

Je repère les coordonnées des points I et J.

\hspace{0.2cm}x_{I}\hspace{0.05cm}y_{I}\hspace{0.05cm}z_{I}\hspace{2.1cm}x_{J}\hspace{0.05cm}y_{J}\hspace{0.05cm}z_{J}

I(\frac{1}{2};0;1)\hspace{2cm}J(1;\frac{1}{2};0)

J’écris la formule :

\overrightarrow{IJ}(x_{J}-x_{I};y_{J}-y_{I};z_{J}-z_{I})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{IJ}(1-\frac{1}{2};\frac{1}{2}-0;0-1)\\\overrightarrow{IJ}(\frac{1}{2};\frac{1}{2};-1)

On ne calcule pas les coordonnées du vecteur \overrightarrow{AE}. Comme A est l’origine du repère, le vecteur \overrightarrow{AE} a les mêmes coordonnées que le point E.

\overrightarrow{AE}(0;0;1)

On ne calcule pas les coordonnées du vecteur \overrightarrow{AC}. Comme A est l’origine du repère, le vecteur \overrightarrow{AC} a les mêmes coordonnées que le point C.

\overrightarrow{AC}(1;1;0).

Pour montrer que les vecteurs \overrightarrow{IJ} , \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires, il faut montrer que l’un est une combinaison linéaire des deux autres.

En examinant les coordonnées des trois vecteurs, on voit que celles de \overrightarrow{AC} sont égales à deux fois celles de \overrightarrow{IJ} plus deux fois celles de \overrightarrow{AE}.

Ainsi \overrightarrow{AC}=2\overrightarrow{IJ}+2\overrightarrow{AE}.

Donc les vecteurs \overrightarrow{IJ} , \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires.

 

La droite d_1 dont la représentation paramétrique est ci-dessous, a pour vecteur directeur le vecteur de coordonnées  (1;-2;3)

La droite d_2 dont la représentation paramétrique est ci-dessous, a pour vecteur directeur le vecteur de coordonnées  (1;1;2)

Les coordonnées  (1;-2;3) et (1;1;2) ne sont pas proportionnelles donc les vecteurs directeurs ne sont pas colinéaires donc d_1 et d_2 ne sont pas parallèles.

 

Pour montrer que la droite d_2 est parallèle au plan P, on va montrer qu’un vecteur directeur \overrightarrow{u_2} de d_2 est orthogonal à un vecteur normal \overrightarrow{n}de P.

\overrightarrow{u_2}(1;1;2) ( voir question précédente).

Comme P a pour  équation x+3y-2z=0 alors \overrightarrow{n} a pour coordonnées (1;3;-2)

On calcule ensuite \overrightarrow{u_2}.\overrightarrow{n}.

Pour calculer \overrightarrow{u_2}.\overrightarrow{n}, on remplace

x par  1 ,  y par 1 ,  z par 2.

Et

 x’ par 1 ,  y’ par 3 ,  z’ par -2.

Dans

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{u_2}.\overrightarrow{n}=1\times 1+1\times 3+2\times (-2)\\\overrightarrow{u_2}.\overrightarrow{n}=1+3-4\\\overrightarrow{u_2}.\overrightarrow{n}=0

Donc les vecteurs \overrightarrow{u_2} et \overrightarrow{n} sont orthogonaux. Comme le vecteur \overrightarrow{n} est orthogonal au plan P.

Alors  d_2 est parallèle à P

 

Il faut montrer que le point L(4;0;3)est le projeté orthogonal du point M(5;3;1) sur le plan P.

  • Montrons d’abord que le vecteur \overrightarrow{LM} est orthogonal au plan P en montrant qu’il est colinéaire au vecteur \overrightarrow{n}(1;3;-2) vu dans la question précédente.

On calcule les coordonnées du vecteur \overrightarrow{LM}.

Je repère les coordonnées des points L et M.

\hspace{0.2cm}x_{L}\hspace{0.05cm}y_{L}\hspace{0.05cm}z_{L}\hspace{2.1cm}x_{M}\hspace{0.05cm}y_{M}\hspace{0.05cm}z_{M}

L(4;0;3)\hspace{2cm}M(5;3;1)

J’écris la formule :

\overrightarrow{LM}(x_{M}-x_{L};y_{M}-y_{L};z_{M}-z_{L})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{LM}(5-4;3-0;1-3)

\overrightarrow{LM}(1;3;-2)

Comme \overrightarrow{LM} et \overrightarrow{n} sont égaux, \overrightarrow{LM} est bien orthogonal au plan P.

  • Montrons ensuite que le point  L appartient au plan P.

Montrons que les coordonnées du point L vérifient l’équation du plan P.

x_L+3y_L-2z_L+2=4+3\times 0-2\times 3+2 \\\hspace{3cm}=4+0-6+2 \\\hspace{3cm}=0

Donc le point  L appartient au plan P.

Donc le point Lest le projeté orthogonal du point M sur le plan P.

 

 

Pour déterminer les coordonnées d’un point , il faut :

Partir de l’origine  A  pour se rendre au point  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

A est l’origine du repère donc A(0;0;0)

On part de  A, pour aller à B on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc B(1;0;0)

On part de  A, pour aller à C on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc C(1;1;0)

On part de  A, pour aller à D on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc D(0;1;0)

On part de  A, pour aller à E on se déplace de  0\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc E(0;0;1)

On part de  A, pour aller à F on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc F(1;0;1)

On part de  A, pour aller à G on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc G(1;1;1)

On part de  A, pour aller à H on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc H(0;1;1)

 

 

Les trois côtés du triangle EGD (en bleu sur la figure) sont trois diagonales de trois carrés de côté  1. Ils ont donc même longueur : \sqrt{2} et le triangle EGD est donc équilatéral.

On a montré dans la question précédente que le triangle EGD est équilatéral de côté \sqrt{2}.

On admet dans cette question que l’aire d’un triangle équilatéral de côté c est égale à \frac{\sqrt{3}}{4}c^2.

Pour calculer l’aire de EGD, on remplace c par \sqrt{2} dans \frac{\sqrt{3}}{4}c^2.

Aire(BGE)=\frac{\sqrt{3}}{4}\sqrt{2}^2\\Aire(BGE)=\frac{\sqrt{3}}{4}\times 2\\Aire(BGE)=\frac{\sqrt{3}}{2}

M est défini par \overrightarrow{BM}=\frac{1}{3}\overrightarrow{BH}

On cherche les coordonnées du point M , on ne les connaît pas, on les nomme (x;y;z).

Les coordonnées des vecteurs \overrightarrow{BM} et \frac{1}{3}\overrightarrow{BH} sont égales.

On exprime les coordonnées du vecteur \overrightarrow{BM}.

Je repère les coordonnées des points B et M.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{M}\hspace{0.05cm}y_{M}\hspace{0.05cm}z_{M}

B(1;0;0)\hspace{2cm}M(x;y;z)

J’écris la formule :

\overrightarrow{BM}(x_{M}-x_{B};y_{M}-y_{B};z_{M}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BM}(x-1;y-0;z-0)

\overrightarrow{BM}(x-1;y;z)

On calcule les coordonnées du vecteur \frac{1}{3}\overrightarrow{BH}.

Je repère les coordonnées des points B et H.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{H}\hspace{0.05cm}y_{H}\hspace{0.05cm}z_{H}

B(1;0;0)\hspace{2cm}H(0;1;1)

J’écris la formule :

\overrightarrow{BH}(x_{H}-x_{B};y_{H}-y_{B};z_{H}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BH}(0-1;1-0;1-0)

\overrightarrow{BH}(-1;1;1)

\frac{1}{3}\overrightarrow{BH}(\frac{1}{3}\times {(-1)};\frac{1}{3}\times {1};\frac{1}{3}\times {1})

\frac{1}{3}\overrightarrow{BH}(-\frac{1}{3};\frac{1}{3};\frac{1}{3})

Les coordonnées des vecteurs \overrightarrow{BM} et \frac{1}{3}\overrightarrow{BH} sont égales.

x-1=-\frac{1}{3}

x=-\frac{1}{3}+1

x=-\frac{1}{3}+1\times \frac{3}{3}

x=-\frac{1}{3}+\frac{3}{3}\\x=\frac{2}{3}

y=\frac{1}{3}

z=\frac{1}{3}

Donc le point M a pour coordonnées (\frac{2}{3};\frac{1}{3};\frac{1}{3}).

 

 

Pour montrer que le vecteur  \overrightarrow{n}(-1;1;1) est normal au plan (EGD), on va montrer qu’il est orthogonal aux vecteurs non colinéaires  \overrightarrow{EG} et \overrightarrow{ED}.

On commence par calculer les coordonnées des vecteurs \overrightarrow{EG} et \overrightarrow{ED}.

On calcule les coordonnées du vecteur \overrightarrow{EG}.

Je repère les coordonnées des points E et G.

\hspace{0.2cm}x_{E}\hspace{0.05cm}y_{E}\hspace{0.05cm}z_{E}\hspace{2.1cm}x_{G}\hspace{0.05cm}y_{G}\hspace{0.05cm}z_{G}

E(0;0;1)\hspace{2cm}G(1;1;1)

J’écris la formule :

\overrightarrow{EG}(x_{G}-x_{E};y_{G}-y_{E};z_{G}-z_{E})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{EG}(1-0;1-0;1-1)

\overrightarrow{EG}(1;1;0)

On calcule les coordonnées du vecteur \overrightarrow{ED}.

Je repère les coordonnées des points E et D.

\hspace{0.2cm}x_{E}\hspace{0.05cm}y_{E}\hspace{0.05cm}z_{E}\hspace{2.1cm}x_{D}\hspace{0.05cm}y_{D}\hspace{0.05cm}z_{D}

E(0;0;1)\hspace{2cm}D(0;1;0)

J’écris la formule :

\overrightarrow{ED}(x_{D}-x_{E};y_{D}-y_{E};z_{D}-z_{E})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{ED}(0-0;1-0;0-1)

\overrightarrow{ED}(0;1;-1)

Ensuite on calcule les produit scalaires  \overrightarrow{n}.\overrightarrow{EG} et \overrightarrow{n}.\overrightarrow{ED}.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{EG}.

\overrightarrow{n}(-1;1;1).

\overrightarrow{EG}(1;1;0).

Pour calculer  \overrightarrow{n}.\overrightarrow{EG}, on remplace : 

 x par -1 ,  y par 1 ,  z par 1.

 x’ par 1 ,  y’ par 1 ,  z’ par 0, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{EG}=(-1)\times 1+1\times 1+1\times 0\\\overrightarrow{n}.\overrightarrow{EG}=-1+1+0\\\overrightarrow{n}.\overrightarrow{EG}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{EG} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{ED}.

\overrightarrow{n}(-1;1;1).

\overrightarrow{ED}(0;1;-1).

Pour calculer  \overrightarrow{n}.\overrightarrow{ED}, on remplace : 

 x par -1 ,  y par 1 ,  z par 1.

 x’ par 0 ,  y’ par 1 ,  z’ par -1, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{ED}=(-1)\times 0+1\times 1+1\times (-1)\\\overrightarrow{n}.\overrightarrow{ED}=0+1-1\\\overrightarrow{n}.\overrightarrow{ED}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{ED} sont orthogonaux.

Le vecteur   \overrightarrow{n} est orthogonal à   \overrightarrow{EG} et \overrightarrow{ED}, donc il est normal au plan (EGD)

 

 

On veut en déduire qu’une équation cartésienne du plan (EGD) est : -x+y+z-1=0

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{n} a pour coordonnées (-1;1;1).

On remplace a par -1 et b par 1 et c par 1 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (EGD) est de la forme :

(-1)\times x+1\times y+1\times z+d=0

-x+y+z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(EGD) passe par E(0;0;1), on remplace x par 0,  y par 0 et z par 1 dans -x+y+z+d=0.

-0+0+1+d=0

1+d=0

d=-1

Une équation cartésienne du plan  (EGD) est -x+y+z-1=0

 

 

d est la droite passant par M et orthogonale au plan (EGD).
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (EGD), alors le vecteur normal au plan  \overrightarrow{n}(-1;1;1) est un vecteur directeur de la droite d.

De plus la droite d passe par le point M(\frac{2}{3};\frac{1}{3};\frac{1}{3}).

On remplace x_M par \frac{2}{3}, y_M par \frac{1}{3}, z_M par \frac{1}{3} ,a par (-1), b par 1 et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

 

Soit K, le pied de la hauteur de la pyramide GEDM issue du point M. Donc K est le point d’intersection de la droite d et du plan (GED). 

K\in d donc ses coordonnées vérifient le système 

K\in (GED) donc ses coordonnées vérifient l’équation -x+y+z-1=0 

Comme K est le point d’intersection de la droite d et du plan (GED). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

-(\frac{2}{3}-t)+(\frac{1}{3}+t)+(\frac{1}{3}+t)-1=0\\-\frac{2}{3}+t+\frac{1}{3}+t+\frac{1}{3}+t-1=0\\3t-1=0\\3t=1\\t=\frac{1}{3}

Pour trouver les valeurs de x,y,z, on remplace t par \frac{1}{3} dans les 3 premières équations.

x=\frac{2}{3}-\frac{1}{3}\\x=\frac{1}{3}
y=\frac{1}{3}+\frac{1}{3}\\y=\frac{2}{3}
z=\frac{1}{3}+\frac{1}{3}\\z=\frac{2}{3}

Donc K a pour coordonnées (\frac{1}{3};\frac{2}{3};\frac{2}{3}).

 

 

On choisit pour base le triangle GED. La hauteur correspondante sera  [MK].

V=\frac{aire(GED)\times MK}{3}

On a vu dans la question 2.b que aire(GED)=\frac{\sqrt{3}}{2}

On calcule MK

M(\frac{2}{3};\frac{1}{3};\frac{1}{3})\\K(\frac{1}{3};\frac{2}{3};\frac{2}{3})

Pour calculer la distance MK, on remplace x_K par \frac{1}{3} , y_K par \frac{2}{3} , z_K par \frac{2}{3} , x_M par \frac{2}{3} , y_M par \frac{1}{3} et z_M par \frac{1}{3} dans la formule

MK=\sqrt{(x_K-x_M)^2+(y_K-y_M)^2+(z_K-z_M)^2}

MK=\sqrt{(\frac{1}{3}-\frac{2}{3})^2+(\frac{2}{3}-\frac{1}{3})^2+(\frac{2}{3}-\frac{1}{3})^2}

On effectue ce qu’il y a entre parenthèses 

MK=\sqrt{(-\frac{1}{3})^2+(\frac{1}{3})^2+(\frac{1}{3})^2}

On effectue les puissances

MK=\sqrt{\frac{1}{9}+\frac{1}{9}+\frac{1}{9}}

On ajoute 

MK=\sqrt{\frac{3}{9}}\\MK=\frac{\sqrt{3}}{\sqrt{9}}\\MK=\frac{\sqrt{3}}{3}

On remplace aire(GED) par \frac{\sqrt{3}}{2} et MK par \frac{\sqrt{3}}{3} dans V=\frac{aire(GED)\times MK}{3}.

V=\frac{\frac{\sqrt{3}}{2}\times \frac{\sqrt{3}}{3}}{3}

V=\frac{\frac{\sqrt{3}^2}{6}}{3}

V=\frac{\frac{3}{6}}{3}

V=\frac{3}{6}\times \frac{1}{3}

V=\frac{1}{6}

 

 

Pour déterminer les coordonnées d’un point, il faut :

Partir de l’origine  A  pour se rendre au point en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{i}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{j}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{k}).

On part de  A pour se rendre en P, on se déplace de  6\overrightarrow{i} puis de  0\overrightarrow{j} et de  0\overrightarrow{k}. 

Donc P(6;0;0) dans le repère  (A; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}).

On part de A pour se rendre en Q, on se déplace de  0\overrightarrow{i} puis de  0\overrightarrow{j} et de  6\overrightarrow{k}. 

Donc Q(0;0;6) dans le repère  (A; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}).

Pour montrer que le vecteur  \overrightarrow{n} est normal au plan (PQR), on va montrer qu’il est orthogonal aux vecteurs non colinéaires  \overrightarrow{PQ} et \overrightarrow{PR}.

On commence par calculer les coordonnées des vecteurs \overrightarrow{PQ} et \overrightarrow{PR}.

On calcule les coordonnées du vecteur \overrightarrow{PQ}.

Je repère les coordonnées des points P et Q.

\hspace{0.2cm}x_{P}\hspace{0.05cm}y_{P}\hspace{0.05cm}z_{P}\hspace{2.1cm}x_{Q}\hspace{0.05cm}y_{Q}\hspace{0.05cm}z_{Q}

P(6;0;0)\hspace{2cm}Q(0;0;6)

J’écris la formule :

\overrightarrow{PQ}(x_{Q}-x_{P};y_{Q}-y_{P};z_{Q}-z_{P})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{PQ}(0-6;0-0;6-0)

\overrightarrow{PQ}(-6;0;6)

On calcule les coordonnées du vecteur \overrightarrow{PR}.

Je repère les coordonnées des points P et R.

\hspace{0.2cm}x_{P}\hspace{0.05cm}y_{P}\hspace{0.05cm}z_{P}\hspace{2.1cm}x_{R}\hspace{0.05cm}y_{R}\hspace{0.05cm}z_{R}

P(6;0;0)\hspace{2cm}R(8;2;8)

J’écris la formule :

\overrightarrow{PR}(x_{R}-x_{P};y_{R}-y_{P};z_{R}-z_{P})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{PR}(8-6;2-0;8-0)

\overrightarrow{PR}(2;2;8)

Ensuite on calcule les produit scalaires  \overrightarrow{n}.\overrightarrow{PQ} et \overrightarrow{n}.\overrightarrow{PR}.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{PQ}.

\overrightarrow{n}(1;-5;1).

\overrightarrow{PQ}(-6;0;6).

Pour calculer  \overrightarrow{n}.\overrightarrow{PQ}, on remplace : 

 x par 1 ,  y par (-5) ,  z par 1.

 x’ par (-6) ,  y’ par 0 ,  z’ par 6, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{PQ}=1\times (-6)+(-5)\times 0+1\times 6\\\overrightarrow{n}.\overrightarrow{PQ}=-6+ 0+ 6\\\overrightarrow{n}.\overrightarrow{PQ}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{PQ} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{PR}.

\overrightarrow{n}(1;-5;1).

\overrightarrow{PR}(2;2;8).

Pour calculer  \overrightarrow{n}.\overrightarrow{PQ}, on remplace : 

 x par 1 ,  y par (-5) ,  z par 1.

 x’ par 2 ,  y’ par 2 ,  z’ par 8, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{PR}=1\times 2+(-5)\times 2+1\times 8\\\overrightarrow{n}.\overrightarrow{PR}=2-10+8\\\overrightarrow{n}.\overrightarrow{PR}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{PR} sont orthogonaux.

Le vecteur   \overrightarrow{n} est orthogonal à   \overrightarrow{PQ} et \overrightarrow{PR}, donc il est normal au plan (PQR)

 

On veut déterminer une équation cartésienne du plan  (PQR) de vecteur normal \overrightarrow{n}.

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{n} a pour coordonnées (1;-5;1).

On remplace a par 1 et b par (-5) et c par 1 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (PQR) est de la forme :

1\times x+(-5)\times y+1\times z+d=0

x-5y+z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(PQR) passe par P(6;0;0), on remplace x par 6,  y par 0 et z par 0 dans x-5y+z+d=0.

6-5\times 0+ 0+d=0

6+d=0

d=-6

Une équation cartésienne du plan  (PQR) est x-5y+z-6=0

I est le centre du cube donc c’est le milieu de [AG].

A(0;0;0) et G(8;8;8).

On remplace x_A, y_A et z_A par 0, x_G par 8, y_G par 8 et z_G par 8 dans 

x_I=\frac{x_A+x_G}{2}\hspace{2cm}y_I=\frac{y_A+y_G}{2}\hspace{2cm}z_I=\frac{z_A+z_G}{2}

x_I=\frac{0+8}{2}\hspace{2.4cm}y_I=\frac{0+8}{2}\hspace{2.4cm}z_I=\frac{0+8}{2}\\x_I=4\hspace{2.8cm}y_I=4\hspace{2.8cm}z_I=4

Donc I(4;4;4).

 

 

On veut déterminer une représentation paramétrique de la droite d perpendiculaire au plan (PQR)
et passant par I.
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (PQR), alors le vecteur normal au plan  \overrightarrow{n}(1;-5;1) est un vecteur directeur de la droite d.

De plus la droite d passe par le point I(4;4;4).

On remplace x_I par 4, y_I par 4, z_I par 4 ,a par 1, b par (-5) et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

 

L est le projeté orthogonal du point I sur le plan (PQR). 

L\in d donc ses coordonnées vérifient le système 

L\in (PQR) donc ses coordonnées vérifient l’équation x-5y+z-6=0 

Comme L est le point d’intersection de la droite d et du plan (PQR). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

(4+t)-5(4-5t)+(4+t)-6=0\\4+t-20+25t+4+t-6=0\\27t-18=0\\27t=18\\t=\frac{18}{27}\\t=\frac{2}{3}

Pour trouver les valeurs de x,y,z, on remplace t par \frac{2}{3} dans les 3 premières équations.

x=4+\frac{2}{3}\\x=4\times \frac{3}{3}+\frac{2}{3}\\x= \frac{12}{3}+\frac{2}{3}\\x= \frac{14}{3}
y=4-5\times \frac{2}{3}\\y=4-\frac{10}{3}\\y=4\times \frac{3}{3}-\frac{10}{3}\\y= \frac{12}{3}-\frac{10}{3}\\y= \frac{2}{3}
z=4+\frac{2}{3}\\z=4\times \frac{3}{3}+\frac{2}{3}\\z= \frac{12}{3}+\frac{2}{3}\\z= \frac{14}{3}

Donc L a pour coordonnées (\frac{14}{3};\frac{2}{3};\frac{14}{3}).

 

 

On cherche quel point se trouve sur la droite d de représentation paramétrique :

a. M(2;1;-1)

b. N(-3;-4;6)

c. P(-3;-4;2)

d. Q(-5;-5;1)

Regardons si M est sur d. On peut, par exemple, déterminer pour quelle valeur de t, y=1.

y=1 si -2+t=1\\\hspace{2.1cm}t=1+2\\\hspace{2.1cm}t=3

On remplace ensuite t par le résultat trouvé  3 dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par 2 et t par 3 dans x=1+2t et on regarde si l’égalité est vérifiée.

2\ne 1+2\times3 donc M(2;1;-1) n’est pas sur d

Regardons si N est sur d. On peut, par exemple, déterminer pour quelle valeur de t, y=-4.

y=-4 si -2+t=-4\\\hspace{2.1cm}t=-4+2\\\hspace{2.1cm}t=-2

On remplace ensuite t par le résultat trouvé  (-2) dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par -3 et t par -2 dans x=1+2t et on regarde si l’égalité est vérifiée.

-3= 1+2\times(-2).

On remplace z par 6 et t par -2 dans z=4-t et on regarde si l’égalité est vérifiée.

6= 4-(-2).

donc N(-3;-4;6) est sur d.

La bonne réponse est la réponse b.

a. (1.5;0.5;1)

b. (-1;-1;2)

c. (1;1;-2)

d. (3;1;2)

On calcule les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(1;0;2)\hspace{2cm}B(2;1;0)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(2-1;1-0;0-2)

\overrightarrow{AB}(1;1;-2)

La bonne réponse est la réponse c.

On cherche une représentation paramétrique de la droite (AB) :

Réponse a

Réponse b

Réponse c

Réponse d

(AB) est la droite passant par A(1;0;2) et de vecteur directeur \overrightarrow{AB}(1;1;-2).  
On remplace x_A par 1, y_A par 0, z_A par 2 ,a par 1, b par 1 et c par -2 dans la représentation paramétrique :

La bonne réponse est la réponse d.

 

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.