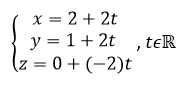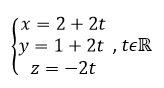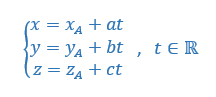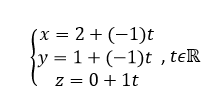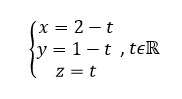logo

T. Représentations paramétriques de droites

Propriété 

Soient A(x_A;y_A;z_A) un point de l’espace et \overrightarrow{u}(a;b;c) un vecteur non nul de l’espace.

On considère la droite d de vecteur directeur \overrightarrow{u} et qui passe par le point A.

Soit M(x;y;z) un point de l’espace.

Le point M appartient à la droite d si et seulement s’il existe un réel t tel que  

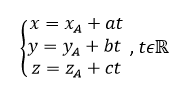
Ce système est une représentation paramétrique de la droite d.

Exercice n°1 

On considère les points   A(2;1;0) , B(4;3;-2) et C(1;0;1)

1.a. déterminer par le calcul les coordonnées du vecteur \overrightarrow{AB}

Pour conjecturer les coordonnées du vecteur \overrightarrow{AB} à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées du vecteur \overrightarrow{AB}(2;2;-2).

correction

1.b. En déduire une représentation paramétrique de la droite (AB)

Pour conjecturer une représentation paramétrique de la droite (AB) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite (AB)  :  X=(2,1,0)+\lambda (2,2,-2).

correction

1.c. Parmi les points suivants : E(2;1;0)  et F(2;3;-2). Lesquels sont sur la droite (AB) ?

Pour placer le point E dans le repère à l’aide de la fenêtre active géogébra ci-dessus, saisir E=(2,1,0) dans la colonne Algèbre située à gauche. Puis regarder si le point est sur la droite (AB).

correction

2.a. déterminer par le calcul les coordonnées du vecteur \overrightarrow{AC}

Pour conjecturer les coordonnées du vecteur \overrightarrow{AC} à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point C. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées du vecteur \overrightarrow{AC}(-1;-1;1).

correction

2.b. En déduire une représentation paramétrique de la droite (AC)

Pour conjecturer une représentation paramétrique de la droite (AC) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point C . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite (AC)  :  X=(2,1,0)+\lambda (-1,-1,1).

correction

2.c. Parmi les points suivants : G(-1;-2;3)  et H(0;-1;-2). Lesquels sont sur la droite (AC) ?

Pour placer le point G dans le repère à l’aide de la fenêtre active géogébra ci-dessus, saisir G=(-1,-2,3) dans la colonne Algèbre située à gauche. Puis regarder si le point est sur la droite (AC).

correction

3. Etudier la position des droites (AB) et (AC)? Qu’en déduire pour les points A,B et C ?

correction

Exercice n°2 

Soient A(0;8;0) et  B(2;-2;2) deux points de l’espace.

Soit la droite d de représentation paramétrique :

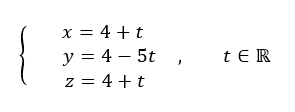
La droite d est-elle parallèle à la droite (AB) ?

correction

Exercice n°3 

Soient A(0;2;4) un point de l’espace.

Soit la droite d de représentation paramétrique :

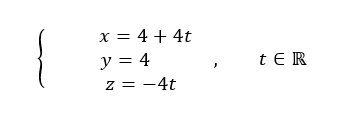
Le point B(0;4;4) est-il le projeté orthogonal de A sur la droite d ?

correction

©2020 – Math’O karé SAS

On calcule les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(2;1;0)\hspace{2cm}B(4;3;-2)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(4-2;3-1;(-2)-0)

\overrightarrow{AB}(2;2;-2)

Pour déterminer une représentation paramétrique de la droite, il faut un vecteur directeur et un point de cette droite.

(AB) passe par A et a pour vecteur directeur  \overrightarrow{AB}.

On remplace x_A par 2, y_A par 1, z_A par 0 ,a par 2, b par 2 et c par -2 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite (AB).

 

Parmi les points suivants : E(2;1;0) et F(2;3;1), lesquels sont sur la droite (AB) dont la représentation paramétrique est :

Regardons si E(2;1;0) est sur (AB). Déterminons, par exemple, pour quelle valeur de t, y=1.

y=1 si 1+2t=1\\\hspace{1.8cm}2t=1-1\\\hspace{1.8cm}2t=0\\\hspace{1.8cm}t=\frac{0}{2}\\\hspace{1.8cm}t=0

On remplace ensuite t par le résultat trouvé  0 dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par 2 et t par 0 dans x=2+2t et on regarde si l’égalité est vérifiée.

2= 2+2\times0 est vraie. 

On remplace z par 0 et t par 0 dans z=-2t et on regarde si l’égalité est vérifiée.

0= -2\times0 est vraie. 

Les trois égalités sont vérifiées avec t=0 donc E(2;1;0) se trouve sur la droite (AB).

Regardons si F(2;3;-2) est sur (AB). Déterminons, par exemple, pour quelle valeur de t, z=-2.

z=-2 si -2t=-2\\\hspace{1.95cm}t=\frac{-2}{-2}\\\hspace{1.95cm}t=1

On remplace ensuite t par le résultat trouvé  1 dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par 2 et t par 1 dans x=2+2t et on regarde si l’égalité est vérifiée.

2\ne 2+2\times1  donc F(2;3;-2) ne se trouve pas sur la droite (AB).

On calcule les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{C}\hspace{0.05cm}y_{C}\hspace{0.05cm}z_{C}

A(2;1;0)\hspace{2cm}C(1;0;1)

J’écris la formule :

\overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A};z_{C}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(1-2;0-1;1-0)

\overrightarrow{AC}(-1;-1;1)

 

Pour déterminer une représentation paramétrique de la droite, il faut un vecteur directeur et un point de cette droite.

(AC) passe par A(2;1;0) et a pour vecteur directeur  \overrightarrow{AC}(-1;-1;1).

On remplace x_A par 2, y_A par 1, z_A par 0 ,a par -1, b par -1 et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite (AC).

Remarque : la représentation donnée par géogébra est exacte aussi car les vecteurs de coordonnées (2;-1;1) et (1;-0.5;0.5) sont colinéaires.

Parmi les points suivants : G(-1;-2;3) et H(0;-1;-2), lesquels sont sur la droite (AC) dont la représentation paramétrique est :

Regardons si G(-1;-2;3) est sur (AC). Déterminons, par exemple, pour quelle valeur de t, z=3.

z=3 si t=3

On remplace ensuite t par le résultat trouvé  3 dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par (-1) et t par 3 dans x=2-t et on regarde si l’égalité est vérifiée.

(-1)= 2-3 est vraie. 

On remplace y par (-2) et t par 3 dans y=1-t et on regarde si l’égalité est vérifiée.

(-2)= 1-3 est vraie. 

Les trois égalités sont vérifiées avec t=3 donc G(-1;-2;3) se trouve sur la droite (AC).

Voyons si H(0;-1;-2) est sur (AC). Déterminons, par exemple, pour quelle valeur de t, z=-2.

z=-2 si t=-2

On remplace ensuite t par le résultat trouvé  (-2) dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par 0 et t par (-2) dans x=2-t et on regarde si l’égalité est vérifiée.

0\ne 2-(-2) donc H(0;-1;-2) ne se trouve pas sur la droite (AC).

 

\overrightarrow{AB} a pour coordonnées  (2;2;-2) et \overrightarrow{AC} a pour coordonnées  (-1;-1;1).

Leurs coordonnées sont proportionnelles donc \overrightarrow{AB} et \overrightarrow{AC} sont colinéaires donc les droites (AB) et (AC) sont parallèles donc les points A,B,C sont alignés.

On calcule les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(0;8;0)\hspace{2cm}B(2;-2;2)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(2-0;(-2)-8;2-0)

\overrightarrow{AB}(2;-10;2)

D’après le cours, les nombres  a,b,c de la représentation paramétrique suivante :

sont les coordonnées d’un vecteur directeur de la droite.

Donc les coordonnées d’un vecteur directeur de la droite d de représentation paramétrique :

sont (1;-5;1)

Les coordonnées de \overrightarrow{AB} sont (2;-10;2) et celles du vecteur directeur de d sont (1;-5;1)).

Les coordonnées sont proportionnelles donc les vecteurs sont colinéaires donc les droites (AB) et d sont parallèles.

 

 

Le point B(0;4;4) est-il le projeté orthogonal de A(0;2;4) sur la droite d de représentation paramétrique :

Regardons d’abord si le vecteur \overrightarrow{AB} est orthogonal à la droite d en montrant qu’il est orthogonal au vecteur \overrightarrow{u}(4;0;-4) qui est un vecteur directeur de d.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(0;2;4)\hspace{2cm}B(0;4;4)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(0-0;4-2;4-4)

\overrightarrow{AB}(0;2;0)

On calcule le produit scalaire  \overrightarrow{u}.\overrightarrow{AB}.

\overrightarrow{u}(4;0;-4).

\overrightarrow{AB}(0;2;0).

Pour calculer  \overrightarrow{u}.\overrightarrow{AB}, on remplace : 

 x par 4 ,  y par 0 ,  z par -4.

 x’ par 0 ,  y’ par 2 ,  z’ par 0, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{u}.\overrightarrow{AB}=4\times 0+0\times 2+(-4)\times 0\\\overrightarrow{u}.\overrightarrow{AB}=0+0+0\\\overrightarrow{u}.\overrightarrow{AB}=0

Donc les vecteurs  \overrightarrow{u} et  \overrightarrow{AB} sont orthogonaux.

Regardons ensuite si le point  B(0;4;4) appartient à la droite d de représentation paramétrique :

Déterminons, par exemple, pour quelle valeur de t, x=0.

x=0 si 4+4t=0\\\hspace{1.8cm}4t=-4\\\hspace{1.94cm}t=-\frac{4}{4}\\\hspace{1.94cm}t=-1

On remplace ensuite  t par le résultat trouvé  (-1) dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace y par 4  dans y=4 et on regarde si l’égalité est vérifiée.

4=4 est vraie. 

On remplace z par 4 et t par (-1) dans z=-4t et on regarde si l’égalité est vérifiée.

4= -4\times(-1) est vraie. 

Les trois égalités sont vérifiées avec t=-1 donc B(0;4;4) se trouve sur la droite d.

On peut donc conclure : le point B(0;4;4) est le projeté orthogonal de A(0;2;4) sur la droite d.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.