Sommaire
Principes additif et multiplicatif. Dénombrement des k-uplets.
Principes additif et multiplicatif.
Définition
Un ensemble fini est un ensemble qui possède un nombre fini d’éléments.
Exemple n°1
L’ensemble des diviseurs de 100 est un ensemble fini, il contient 9 éléments.
Pour s’en convaincre, il suffit d’écrire ce programme sur la TI 83 Python :
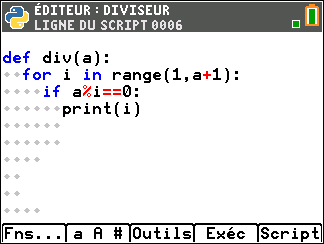
Et d’exécuter ce programme:
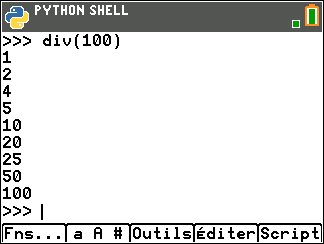
Exemple n°2
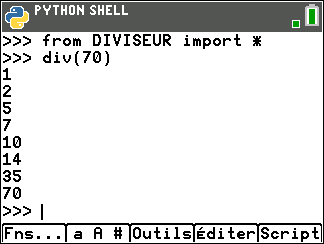
L’ensemble des diviseurs de 70 est un ensemble fini, il contient 8 éléments.
Pour s’en convaincre, on exécute le programme précédent :
Principe additif
Si A et B sont deux parties disjointes d’un ensemble fini F contenant respectivement m et n éléments alors le nombre d’éléments contenus dans la réunion E\cup F est la somme m+n.
Dans certains manuels, card(E) représentant le nombre d’éléments de E, le principe précédent s’écrit :
card(E\cup F)=card(E)+card(F).
Pour aller plus loin : Dans le cas où A et B sont deux parties non disjointes ( cela signifie par exemple qu’il y a p éléments à la fois dans A et B ) d’un ensemble fini F contenant respectivement m et n éléments alors le nombre d’éléments contenus dans la réunion E\cup F est la somme m+n-p.
Qu’on peut aussi écrire :
card(E\cup F)=card(E)+card(F)-card(E\cap F).
Exemple n°3
On jette un dé équilibré à 6 faces.
On note E l’univers de l’expérience, on a E=\{1,2,3,4,5,6\}.
On note A l’évènement obtenir un résultat pair, on a A=\{2,4,6\} donc A contient 3 éléments.
On note B l’évènement obtenir un diviseur de 3, on a B=\{1,3\} donc B contient 2 éléments.
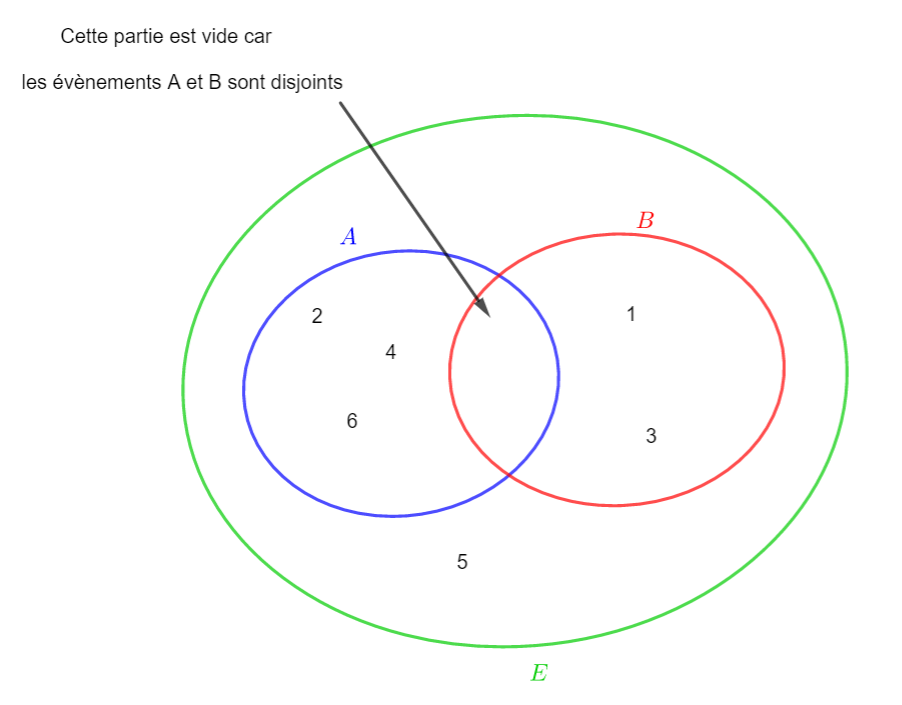
Comme A et B sont disjoints, on applique le principe additif et A\cup B contient 3+2 éléments, c’est-à-dire 5.
Illustration avec un diagramme de Venn :
Définitions
Un couple de deux éléments a et b de E est la donnée de ces deux élèments ( attention l’ordre compte ). On le note (a,b).
Le produit cartésien de E et de F, noté E\times F est l’ensemble des couples (e,f), où e\in E et où f\in F.
Exemple n°4
Un code est constitué d’une lettre et d’un chiffre.
On note L l’ensemble des lettres.
On note C l’ensemble des chiffres.
L’ ensemble de tous les codes possibles sont les couples du produit cartésien L\times C.
Propriété : Principe multiplicatif
Si E contient n éléments et F contient m éléments alors E\times F contient n\times m éléments.
Qu’on peut aussi écrire :
card(E\times F)=card(E)\times card(F)
Suite de l’exemple n°4
L l’ensemble des lettres contient 26 éléments.
On note C l’ensemble des chiffres contient 10 éléments.
Donc le produit cartésien L\times C contient 26\times 10 éléments.
On peut donc créer 260 codes différents.
Dénombrement des k-uplets
Définition
Un k-uplet de E est une liste de k éléments et E. L’ordre compte et on peut retrouver le même élément plusieurs fois.
On note E^{k} l’ensemble des k-uplets de E.
Exemple n°5
On jette une pièce de monnaie 5 fois de suite et on note à chaque fois le résultat visible.
Les issues de l’expérience sont tous les 5-uplets de l’ensemble E=\{P,F\}.
Exemple n°6
Le code PIN d’un smarphone est composé de quatre chiffres.
Les issues de l’expérience sont tous les 4-uplets de l’ensemble E=\{0,1,2,3,4,5,6,7,8,9\}.
Exemple n°7
Un QCM contient dix questions. Pour chacune d’entre elles, il y a quatre réponses possibles A, B, C et D, parmi elles, une seule est exacte.
Une personne décide de répondre au hasard à ce QCM.
Les issues de l’expérience sont tous les 10-uplets de l’ensemble E=\{A,B,C,D\}.
Propriété
Si E contient n éléments, le nombre de k-uplets de E est n^k.
Suite de l’exemple n°5
Les issues de l’expérience sont tous les 5-uplets de l’ensemble E=\{P,F\}, il y en a 2^5=32
Suite de l’exemple n°6
Les issues de l’expérience sont tous les 4-uplets de l’ensemble E=\{0,1,2,3,4,5,6,7,8,9\}, il y en a 10^4=10000.
Suite de l’exemple n°7
Les issues de l’expérience sont tous les 10-uplets de l’ensemble E=\{A,B,C,D\}, il y en a 4^{10}=1048576
Nombre de parties d’un ensemble.
Définition
Une partie de E est un ensemble d’éléments de E.
Exemple n°8
Soit E=\{a,b,c\}.
Les parties de E sont : \varnothing , \{a\} , \{b\} , \{c\} , \{a,b\} , \{a,c\} , \{b,c\} , \{a,b,c\}. Il y a donc huit parties.
Propriété
Si E contient n éléments, le nombre de parties de E est 2^n.
Démonstration
Si E=\{e_1,e_2,e_3,…,e_n\}.
On associe à une partie de l’ensemble E un n-uplet contenant des 1 et des 0 ( on met 1 si le e_i est dans la partie, 0 sinon ) .
Par exemple à \{e_1,e_4\} on associe le n-uplet \{1,0,0,1,0,0,…,0\} , \{e_1,e_3,e_4,e_5\} on associe le n-uplet \{1,0,1,1,1,0,…,0\}, …
Le nombre de parties de E sera égal au nombre de n-uplets de l’ensemble \{0,1\}, c’est-à-dire 2^n.
Dénombrement des k-uplets d’éléments distincts.
Nombre de k-uplets d’éléments distincts.
Propriété
Si E contient n éléments, le nombre de k-uplets d’éléments distincts de E est
n(n-1)(n-2)…(n-k+1).
Illustration de la propriété
Tableau ( méthode des cases)
1er élément | 2ème élément | 3ème élément | 4ème élément | … | (k-1)ème élément | kème élément |
n possibilités | n-1 possibilités | n-2 possibilités | n-3 possibilités | n-(k-2) possibilités | n-(k-1) possibilités |
On multiplie les nombres de la ligne du bas, ainsi le nombre de k-uplets d’éléments distincts de E est bien égal à n(n-1)(n-2)…(n-k+1)
Exemple n°9
Le principe du Quinté est en soit très simple : il s’agit de trouver les 5 premiers chevaux à l’arrivée des courses.
Dans une course comprenant 16 chevaux, pour trouver le nombre de quintés différents, on utilise la propriété précédente.
E contient 16 éléments, le nombre de 5-uplets d’éléments distincts de E est 16\times15\times 14\times13\times12=524160.
Factorielle d’un entier naturel.
Définition
Soit n un entier naturel non nul. On appelle factorielle n, notée n!, le produit de tous les nombres entiers compris entre 1 et n. n!=1\times 2\times3\times4\times…\times n.
Exemple n°10
5!=1\times 2\times 3\times 4\times 5=120.
Avec la TI 83 Premium CE :
Propriété
Si E contient n éléments, le nombre de k-uplets distincts de E est \frac{n!}{(n-k)!}.
Démonstration
\frac{n!}{(n-k)!}=\frac{1\times 2\times3\times4\times…\times(n-k)(n-k+1)\times…\times n}{1\times 2\times3\times4\times…\times (n-k)}On simplifie par 1\times 2\times 3\times4\times…\times (n-k) en haut et en bas
\hspace{0.9cm}=\frac{(n-k+1)\times…\times n}{1}\\\hspace{0.9cm}=(n-k+1)\times…\times nExemple n°11
Dans une urne, se trouvent neuf cartons où sont inscrites les lettres du mot PARTIES.
On tire successivement 4 cartons de l’urne sans remise.
On veut trouver combien de mots de quatre lettres peut-on former ?
On appelle mot de 4 lettres, un 4_uplet de l’ensemble E=\{P,A,R,T;I,E;S\}.
On remplace k par 4 et n par 9 dans la phrase le nombre de k-uplets distincts de E est \frac{n!}{(n-k)!}
le nombre de 4-uplets distincts de E est
\frac{9!}{(9-5)!}=\frac{9!}{4!}
\hspace{0.9cm}=\frac{362880}{24}
\hspace{0.9cm}=15120
Nombre de permutations.
Définition
Une permutation d’un ensemble E à n éléments est un n-uplet d’éléments distincts de E.
Exemple n°12
Trois amis : Alain, Bernard et Cyril décident d’aller au cinéma. Dans leur ville, se trouvent trois cinémas.
Ils décident que chacun se rendra seul dans un cinéma.
Pour trouver toutes les possibilités, on va dénombrer les 3-uplets d’éléments distincts de l’ensemble E=\{Alain,Bernard,Cyril \}. En sachant que le 3_uplet suivant (Alain,Cyril,Bernard) correspond à la possibilité Alain se rend dans le cinéma n°1, Cyril se rend dans le cinéma n°2 et Bernard se rend dans le cinéma n°3.
Il s’agit donc des permutations d’un ensemble à trois éléments.
Propriété
Si E contient n éléments, le nombre de permutations de E est n\times (n-1)\times (n-2)\times … \times 1 c’est-à-dire n!.
Suite de l’exemple n°12
Comme il s’agit des permutations d’un ensemble à trois éléments, il y en a 3!, c’est-à-dire 6.
Il y a donc pour les trois amis : Alain, Bernard et Cyril, 6 possibilités différentes d’aller au cinéma, en sachant que chacun se rendra seul dans un cinéma.
Combinaisons
Nombre de combinaisons.
Définition
Une combinaison de k éléments d’un ensemble E est une partie de E à k éléments. L’ordre ne compte pas et les éléments sont distincts.
On note \binom{n}{k} le nombre de combinaisons de k éléments de E.
Exemple n°13
On considère l’ensemble E=\{a,b,c\}.
Les parties de E sont :
\varnothing , la seule combinaison de 0 éléments dans un ensemble à 3 éléments.
Remarque : \binom{3}{0}=1.
\{a\} , \{b\} , \{c\} les combinaisons de 1 éléments dans un ensemble à 3 éléments.
Remarque : \binom{3}{1}=3.
\{a,b\} , \{a,c\} , \{b,c\} les combinaisons de 2 éléments dans un ensemble à 3 éléments.
Remarque : \binom{3}{2}=3.
\{a,b,c\} est la seule combinaison de 3 éléments dans un ensemble à 3 éléments.
Remarque : \binom{3}{3}=1.
Propriété
Soit 0\leq k\leq n alors
\binom{n}{k}=\frac{n!}{(n-k)!k!}=\frac{n(n-1)…(n-k+1)}{k!}
Cas particuliers :
\binom{n}{0}=1
\binom{n}{1}=n
\binom{n}{n}=1
Propriétés des combinaisons.
Propriété
Soit 0\leq k\leq n alors
\binom{n}{k}=\binom{n}{n-k}
Triangle de Pascal
Relation de Pascal.
Propriété
Soit 0\leq k\leq n alors
\binom{n}{k}+\binom{n}{k+1}=\binom{n+1}{k+1}
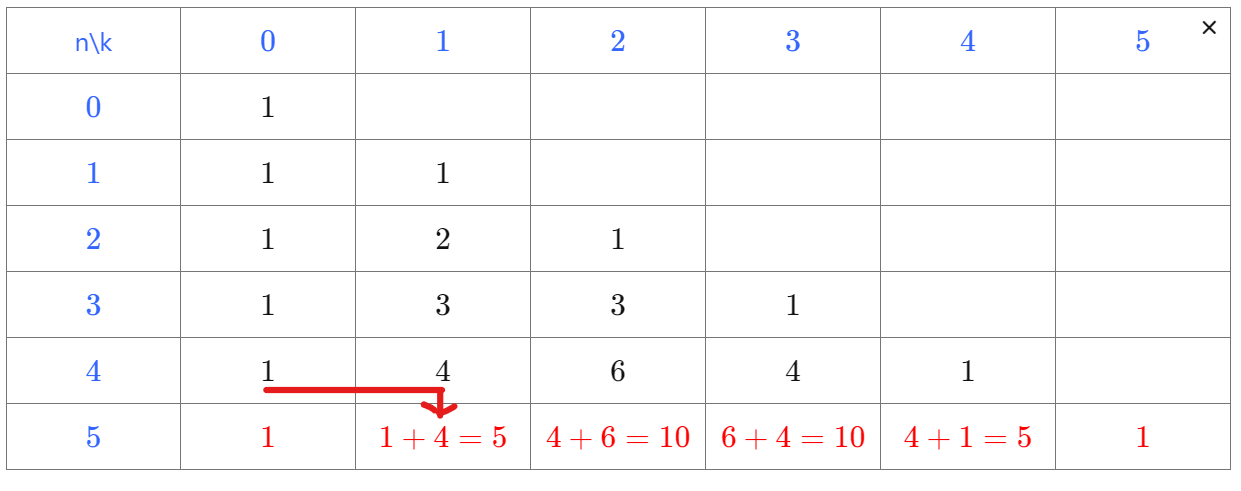
Triangle de Pascal
Après avoir observé, essayer de compléter la dernière ligne
| n\k | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | |||||
| 1 | 1 | 1 | ||||
| 2 | 1 | 2 | 1 | |||
| 3 | 1 | 3 | 3 | 1 | ||
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 |
Pour s’y retrouver dans les tirages…
On tire k objets parmi les n objets d’un ensemble E.
Tirage successif (l’ordre compte)
Tirage simultané (l’ordre ne compte pas)
Avec remise
Les résultats sont des k-uplets, c’est-à-dire des listes ordonnées de k éléments de E (distincts ou non). Il y en a en tout
n^k
Il n’y a pas de tirage simultané avec remise.
Sans remise
Les résultats sont des k-uplets d’éléments distincts, c’est-à-dire des listes ordonnées de k éléments distincts de E ( dans des exercices anciens, on utilise le mot arrangement).
Il y en a en tout
n\times(n-1)\times…\times(n-k+1)
ou
\frac{n!}{(n-k)!}
Cas particulier : quand k=n, il s’agit de permutations de n objets et il y en a
n!
Les résultats sont des combinaisons de k d’éléments de E, c’est-à-dire des parties de k éléments de E. Il y en a
\binom{n}{k}