Sommaire
Principe additif
Exercice n°1 (évènements disjoints)
On jette un dé à 6 faces, on lit sa face supérieure.
On note A, l’évènement obtenir un diviseur de 5.
On note B, l’évènement obtenir un nombre pair.
- Déterminer card(A), le cardinal de l’ensemble A qui correspond au nombre d’éléments de A
2. Déterminer card(B), le cardinal de l’ensemble B qui correspond au nombre d’éléments de B
3. En déduire A\cup B, le cardinal de l’ensemble A\cup B qui correspond au nombre d’éléments de [A\cup B.
Exercice n°2 (évènements disjoints)
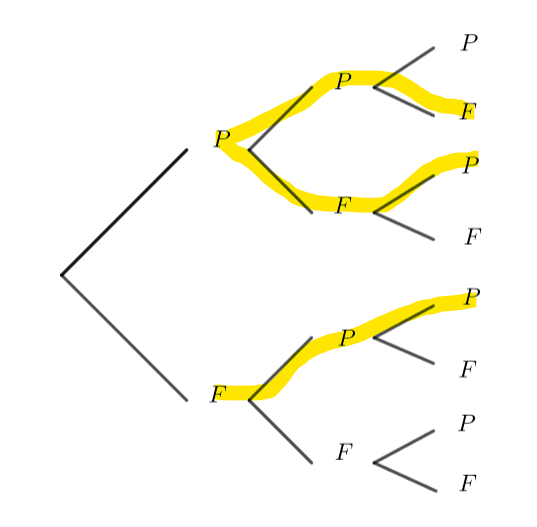
On jette une pièce de monnaie trois fois de suite.
On note A, l’évènement obtenir exactement une fois face.
On note B, l’évènement obtenir le même résultat les trois fois.
- Déterminer card(A), le cardinal de l’ensemble A qui correspond au nombre d’éléments de A
2. Déterminer card(B), le cardinal de l’ensemble B qui correspond au nombre d’éléments de B
3. En déduire A\cup B, le cardinal de l’ensemble A\cup B qui correspond au nombre d’éléments de [A\cup B/latex].
Exercice n°3 (évènements non disjoints)
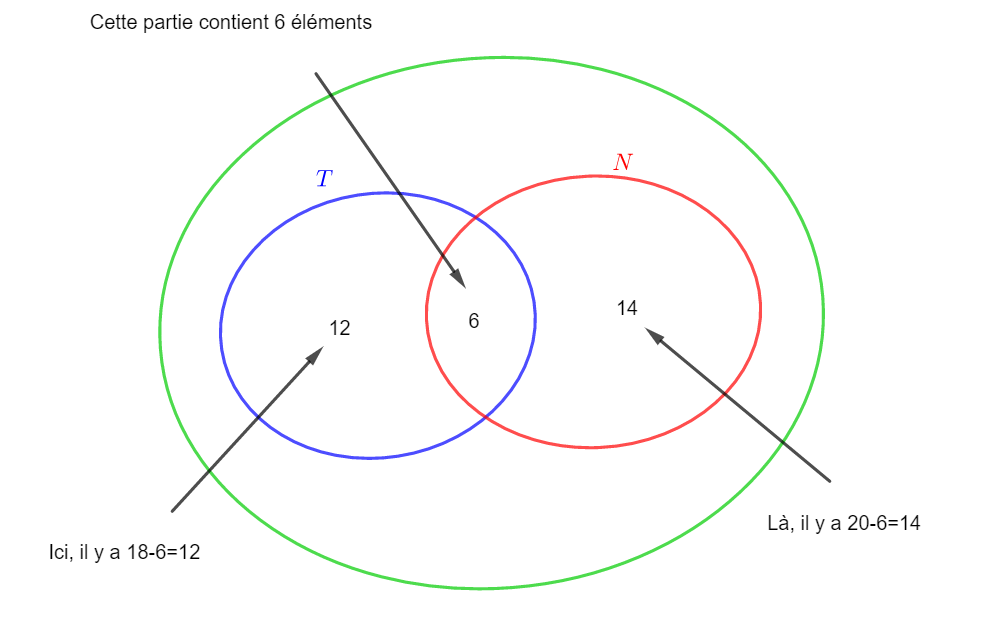
Dans un club de sport, 18 personnes font du tennis , 20 pratiquent la natation et 6 pratiquent les deux sports.
Combien de personnes pratiquent le tennis ou la natation.
On pourra noter T, l’évènement la personne pratique le tennis.
On pourra noter N, l’évènement la personne pratique la natation.
Exercice n°4 (évènements non disjoints)
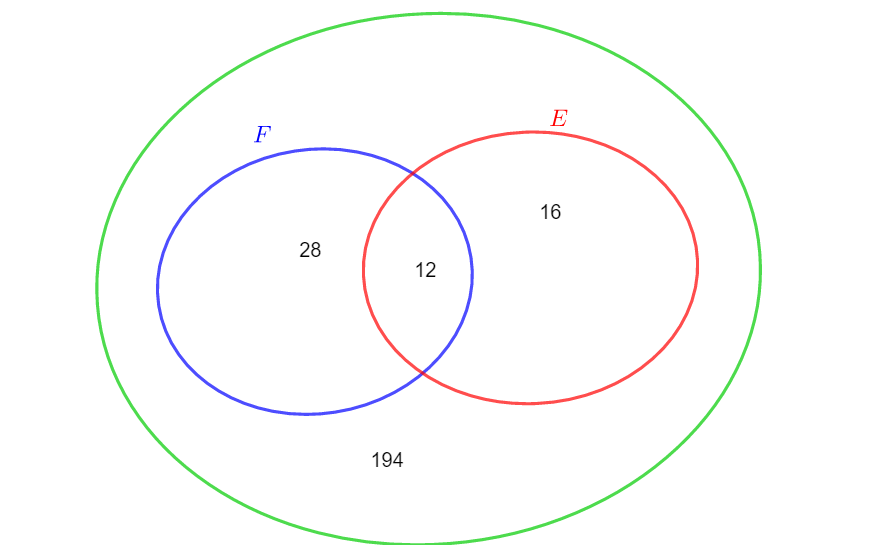
Une entreprise de transport possède 250 véhicules.
Parmi eux 40 ont un défaut de freinage, 28 ont un défaut d’éclairage et 12 présentent les deux.
On pourra noter F, l’évènement le véhicule a un défaut de freinage.
On pourra noter E, l’évènement le véhicule a un défaut d’éclairage.
Combien de véhicules ont un défaut de freinage ou un défaut d’éclairage.
Exercice n°5 (évènements non disjoints)
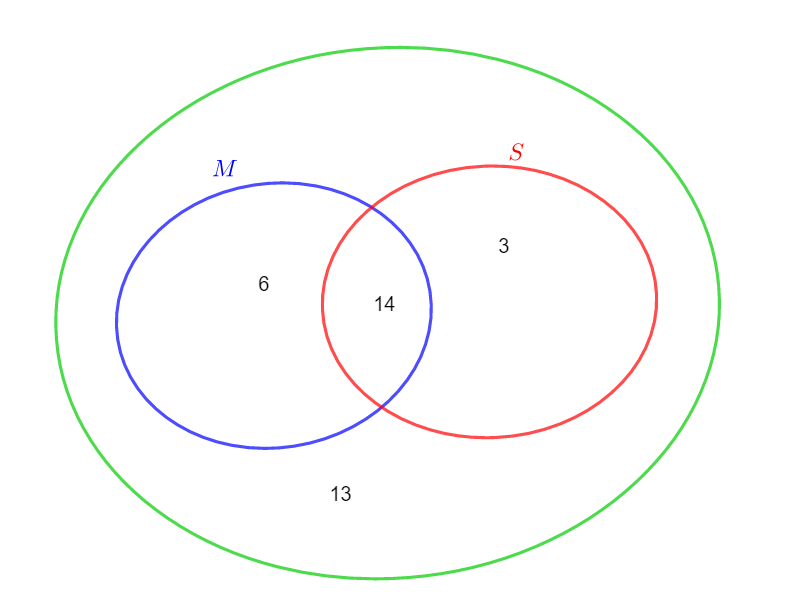
Une classe de première générale compte 36 élèves.
20 ont choisi la spécialité mathématiques, 17 la spécialité SVT et 14 font choisi les deux.
- Combien d’élèves font spécialité mathématiques ou spécialité SVT ?
2. En déduire le nombre d’élèves qui ne font ni spécialité mathématiques , ni spécialité SVT.
Principe multiplicatif
Exercice n°6
Dans un restaurant, on propose une formule plat + dessert à 12 euros.
Les plats proposés sont : entrecôte frites, filet de colin pomme vapeur et saucisse purée.
Les desserts sont tarte tatin et île flottante.
Combien y’a-t-il de possibilités pour la formule à 12 euros.
Exercice n°7
On considère l’ensemble E=\{as,2,3,…,10,valet,dame,roi\} et l’ensemble F=\{\diamondsuit,\heartsuit,\clubsuit,\spadesuit\}.
Que représente l’ensemble E\times F ? Combien possède-t-il d’éléments ?
k-uplets
Exercice n°8
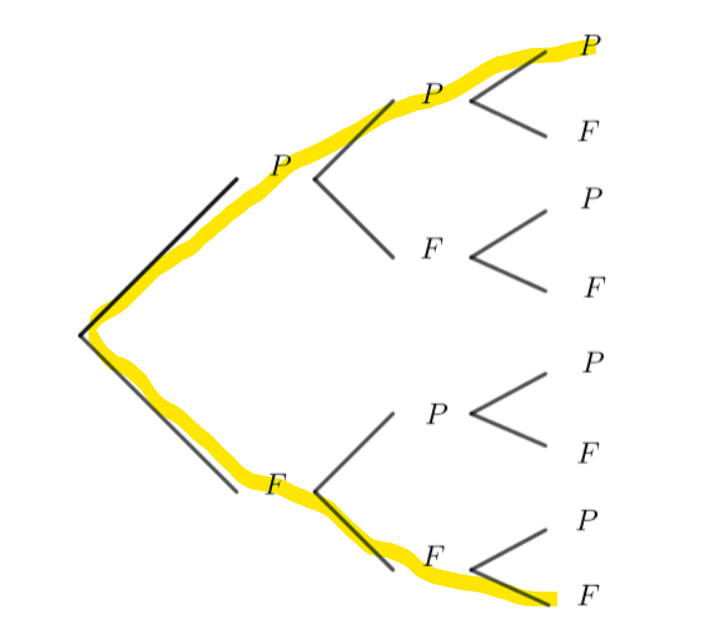
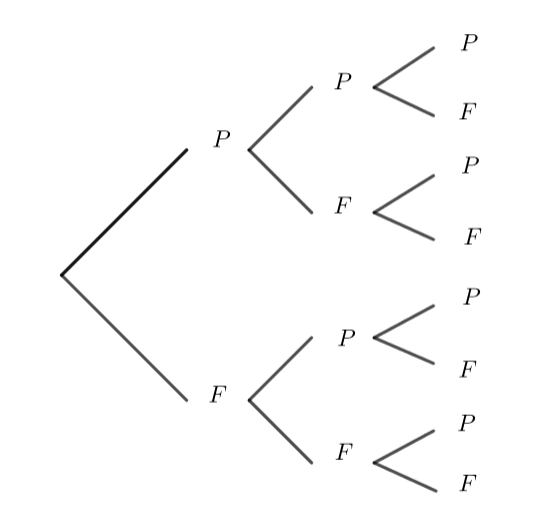
On considère l’ensemble E=\{P,F\}. Combien de 3-uplets de E peut-on former ?
Exercice n°9
Le code d’une valise comporte trois chiffres. Combien de codes peut-on former au total ?
Exercice n°10
On jette un dé huit fois de suite et à chaque fois on note le numéro sur la face supérieure.
Combien d’issues contient l’univers de cette expérience ?
Exercice n°11
Le numéro d’immatriculation d’une voiture comporte
- deux lettres ( on ne peut pas prendre O,I,U)
- trois chiffres entre 0 et 9
- deux lettres ( on ne peut pas prendre O,I,U)
Combien de plaques d’immatriculation différentes peut-on créer ?
Exercice n°12
De combien de façons différentes peut-on ranger 5 paires de chaussettes dans trois tiroirs ?
Il peut y avoir un ou deux tiroirs vides.
Nombre de parties d’un ensemble.
Exercice n°13
Soit l’ensemble E=\{1;2;3;4\}.
- Déterminer toutes les parties de l’ensemble E.
2. Déterminer de deux façons différentes le nombre de parties de l’ensemble E.