Sommaire
Pour s’y retrouver avec les tirages …
On tire k objets parmi les n objets d’un ensemble E.
Tirage successif (l’ordre compte)
Tirage simultané (l’ordre ne compte pas)
Avec remise
Les résultats sont des k-uplets, c’est-à-dire des listes ordonnées de k éléments de E (distincts ou non). Il y en a en tout
n^k
Il n’y a pas de tirage simultané avec remise.
Sans remise
Les résultats sont des k-uplets d’éléments distincts, c’est-à-dire des listes ordonnées de k éléments distincts de E ( dans des exercices anciens, on utilise le mot arrangement).
Il y en a en tout
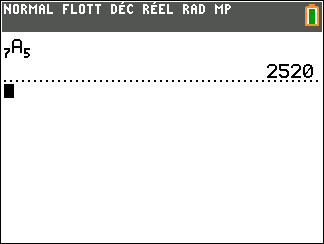
n\times(n-1)\times…\times(n-k+1)
ou
\frac{n!}{(n-k)!}
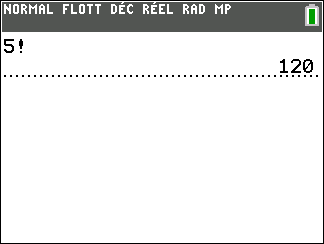
Cas particulier : quand k=n, il s’agit de permutations de n objets et il y en a
n!
Les résultats sont des combinaisons de k d’éléments de E, c’est-à-dire des parties de k éléments de E. Il y en a
\binom{n}{k}
k-uplets d’éléments distincts
Exercice n°1
Parmi les listes suivantes, lesquelles sont des 4-uplets d’éléments distincts de l’ensemble E=\{a;b;c;d;e\}.
- abc
2. abce
3. ab2e
4. abcs
5. aace
6. ebcd
7. 1b2e
8. bcd
Exercice n°2
Dans une urne, se trouvent 6 cartons sur lesquels se trouvent les lettres : N, O, M, B, R, E.
Combien peut-on former de mots différents ( qu’ils aient une signification ou non ) en sortant successivement sans remise 4 cartons de l’urne ?
Exercice n°3
Le principe du Tiercé est en soit très simple : il s’agit de trouver les 3 premiers chevaux dans le bon ordre à l’arrivée des courses.
Dans une course comprenant 15 chevaux, quel est le nombre de tiercés différents qu’on peut faire ?
Exercice n°4
Un sac contient 5 jetons verts (numérotés de 1 à 5) et 4 jetons rouges (numérotés de 1 à 4).
On tire successivement sans remise 3 jetons du sac.
1. Combien y’a-t-il de tirages différents au total ?
2. Combien y’a-t-il de tirages comportant 3 jetons verts ?
3. Combien y’a-t-il de tirages comportant au moins un jeton rouge ?
4. Combien y’a-t-il de tirages comportant exactement un jeton vert ?
Exercice n°5
Une personne décide de louer un coffre à la banque et elle doit composer un code secret composé de six chiffres distincts compris entre 1 et 8.
- Combien y’a-t-il de choix possibles ?
2. Parmi tous les codes possibles, combien commencent par 1.
permutations
Exercice n°6
On veut prendre une équipe de basket en photo.
Les cinq joueurs sont alignés.
Combien y’a-t-il de façons de les disposer ?
Exercice n°7
Combien d’anagrammes du mot DROITE peut-on former ?
Exercice n°8
Une personne vient d’acquérir une encyclopédie composée de 10 tomes.
Si on la range au hasard sur l’étagère de la bibilothèque, combien y’a-t-il de rangements possibles.