On tire k objets parmi les n objets d’un ensemble E.
Tirage successif (l’ordre compte)
Tirage simultané (l’ordre ne compte pas)
Avec remise
Les résultats sont des k-uplets, c’est-à-dire des listes ordonnées de k éléments de E (distincts ou non). Il y en a en tout
n^k
Il n’y a pas de tirage simultané avec remise.
Sans remise
Les résultats sont des k-uplets d’éléments distincts, c’est-à-dire des listes ordonnées de k éléments distincts de E ( dans des exercices anciens, on utilise le mot arrangement).
Il y en a en tout
n\times(n-1)\times…\times(n-k+1)
ou
\frac{n!}{(n-k)!}
Cas particulier : quand k=n, il s’agit de permutations de n objets et il y en a
n!
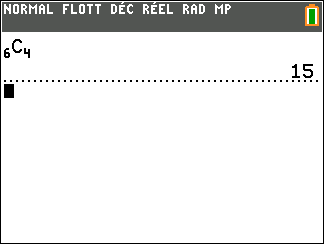
Les résultats sont des combinaisons de k d’éléments de E, c’est-à-dire des parties de k éléments de E. Il y en a
\binom{n}{k}