logo

TE. Nombres complexes : calculs et conjugué.

Sommaire

Ensemble des nombres complexes

Définition 

 Il existe un ensemble noté \mathbf{C} et appelé ensemble des nombres complexes qui vérifie les propriétés suivantes :

  • \mathbf{R}\subset\mathbf{C}
  • L’ensemble \mathbf{C}est muni d’une addition et d’une multiplication qui prolongent celles de \mathbf{R} et les règles de calcul restent les mêmes.
  • Il existe un nombre complexe, noté i, tel que i^2=-1.
  • Tout nombre complexe s’écrit de façon unique sous la forme a+ib avec a et b réels.

Exemples : 3 , i , 3+i , 3i sont des nombres complexes.

Définition 

L’écriture a+ib (avec a et b réels) d’un nombre complexe z s’appelle la forme algébrique d’un complexe 

                    a est appelée la partie réelle de z et est notée Re(z)

                    b est appelée la partie imaginaire de z et est notée Im(z)         .          

Exercice n°1 

Déterminer dans chaque cas, la partie réelle et la partie imaginaire de z.

z=3+2i
correction
z=-1+i
correction
z=-2i+6
correction
z=9
correction
z=4i
correction
z=-5i
correction
z=3i-2
correction
z=i
correction

Remarque :

Si Re(z)=0 , on dit que z est un imaginaire pur.

Si Im(z)=0 , on dit que z est un réel.

Propriété 

Deux nombres complexes sont égaux  si, et seulement si, ils ont la même partie réelle et la même partie imaginaire.

Opérations sur les nombres complexes

Soient deux nombres complexes z et z’ de formes algébriques respectives z=a+ib et z’=a’+ib’ 

 Définition (l’opposé d’un nombre complexe)

 L’opposé d’un nombre complexe est le nombre complexe -z défini par

-z=-a-ib

Exemples : L’opposé de 3+2i est  -3-2i, l’opposé de 3-i est  -3+i et l’opposé de -6-2i est  6+2i.

Propriétés ( somme et produit de nombres complexes )

z+z’=(a+a’)+i(b+b’)

z.z’=(aa’-bb’)+i(ab’+a’b)

Démonstration de la formule du produit

Voici le début de la démonstration :

z.z’=(a+ib)(a’+ib’)

On développe

\hspace{0.6cm}=aa’+…

correction

Les calculs avec des nombres complexes avec la TI 83 premium CE.

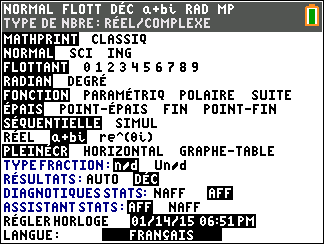
Appuyer sur la touche mode du clavier de la calculatrice.

Sur la 8ème ligne sélectionner a+bi.

Quand on tape des calculs avec la calculatrice, pour obtenir le i, taper sur la touche 2nde puis sur la touche . située entre 0 et (-) .

Exercice n°2 

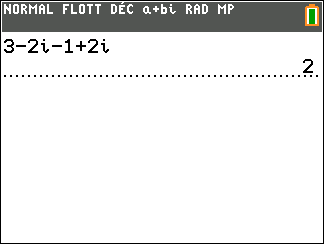
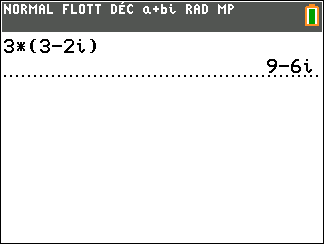
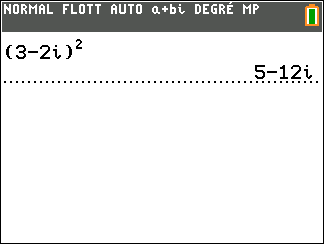
On considère  z_1=3-2i et z_2=-1+2i

Déterminer la forme algébrique des complexes suivants.

z_1+z_2
correction
3z_1
correction
z_1\times z_2
correction
(z_1)^2
correction

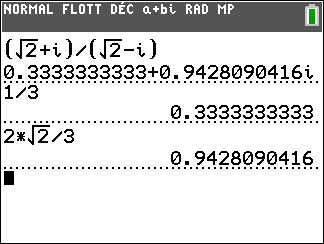
Exercice n°3

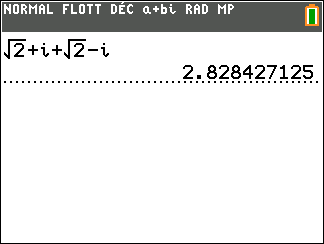
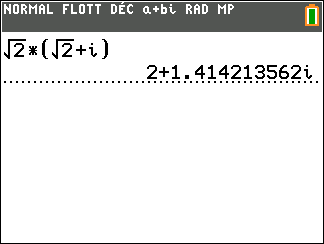
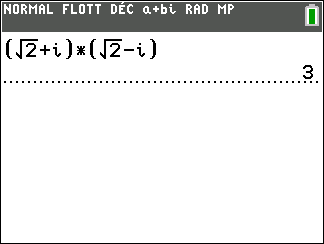
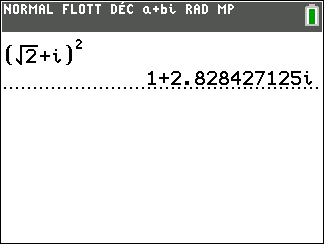
On considère  z_1=\sqrt{2}+i et z_2=\sqrt{2}-i

Déterminer la forme algébrique des complexes suivants.

z_1+z_2
correction
z=\sqrt{2}z_1
correction
z_1\times z_2
correction
(z_1)^2
correction

Résoudre des équations dans C avec Géogébra.

Ouvrir une page de Calcul Formel comme ci-dessous ( elle est active, vous pouvez l’utiliser ).

Saisir CSolutions(équation,variable) puis faire entrer.

Pour saisir i, il faut appuyer sur les touches Alt et i .

On l’utilise pour conjecturer les résultats de l’exercice n°4 ci-dessous.

Exercice n°4 

Résoudre les équations suivantes dans \mathbf{C}.

1+2i+z=2+i
correction
4+2z=3-i
correction
2i-3z=3-i
correction
3+i-2z=5+3i
correction

Définition  et propriété ( inverse d’un nombre complexe non nul )

Tout nombre complexe non nul z de forme algébrique z=a+ib  admet un inverse noté \frac{1}{z} de forme algébrique

\frac{1}{z}=\frac{a}{a^2+b^2}+i\frac{(-b)}{a^2+b^2}

Démonstration de la formule de l’inverse

Voici le début de la démonstration :

\frac{1}{z}=\frac{1}{a+ib}

On multiplie le second membre par  \frac{a-ib}{a-ib}

\hspace{0.3cm}=\frac{1}{a+ib}\times \frac{a-ib}{a-ib}

correction

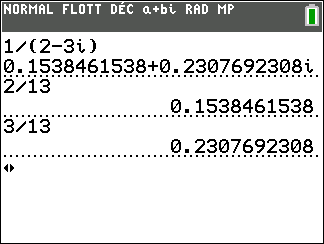
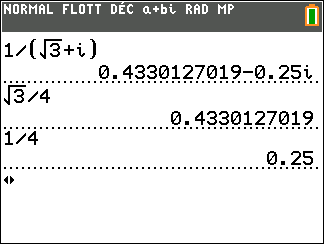
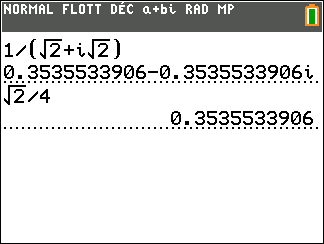
Exercice n°5

Déterminer la forme algébrique de l’inverse des nombres complexes suivants.

z=1+i
correction
z=2-3i
correction
z=\sqrt{3}+i
correction
z=\sqrt{2}+i\sqrt{2}
correction

Définition ( quotient de deux complexes )

Soient deux nombres complexes z et z’ tels que z’ soit non nul.

Alors le quotient \frac{z}{z’} est égal à z\times \frac{1}{z’}.

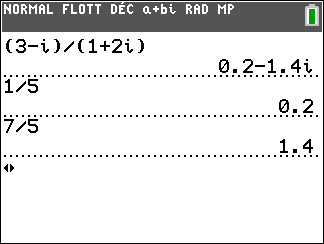
Exercice n°6 

Déterminer dans chaque cas, la partie réelle et la partie imaginaire des nombres complexes suivants.

z_1=\frac{3}{1-i}
correction
z_2=\frac{3-i}{1+2i}
correction
z_3=\frac{\sqrt{2}+i}{\sqrt{2}-i}
correction
z_4=\frac{1+5i}{-2+i}
correction

Exercice n°7 

Résoudre les équations suivantes dans \mathbf{C}.

(1+i)z=2+i
correction
iz=3-i
correction
(1+2i)z=3-2i
correction
2iz=5+3i
correction

Conjugué d’un nombre complexe  

 Définition (conjugué d’un nombre complexe)

Soit z un nombre complexe tel que z=a+ib

Le conjugué de z noté \overline{z} est le nombre complexe défini par

\overline{z}=a-ib.

Exemples : Le conjugué de z=3+2i est \overline{z}=3-2i, le conjugué de z=2i est \overline{z}=-2i et le conjugué de z=3 est \overline{z}=3. 

Calculer le conjugué avec la TI 83 premium CE.

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

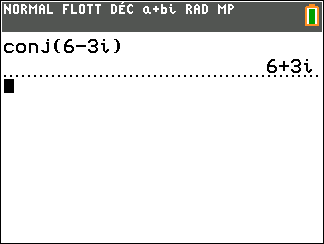
Sur la 1ère ligne sélectionner conj( et saisir à al suite le nombre complexe.

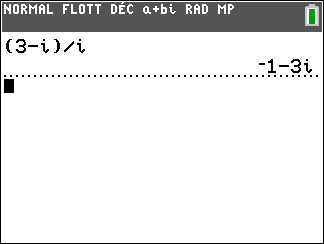
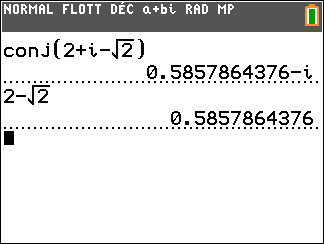
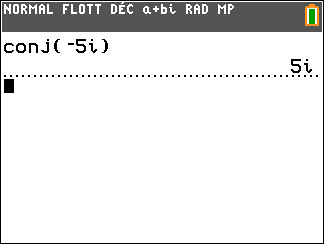
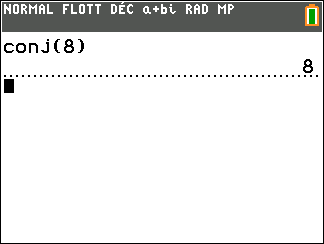
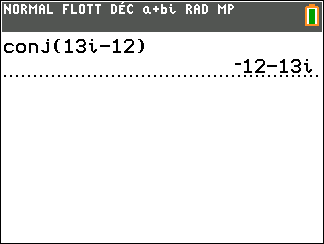
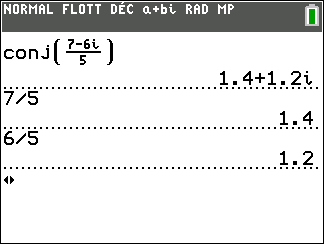
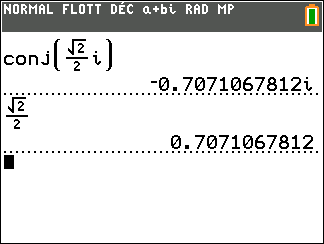
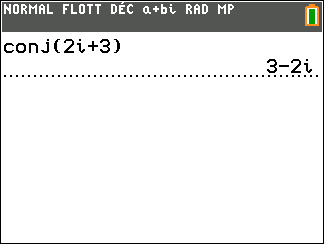
Conjecturons le conjugué du premier complexe de l’exercice n°8

 

Exercice n°8

Déterminer les conjugués des nombres complexes suivants.

 6-3i

correction

2+i-\sqrt{2}

correction

-5i

correction

8

correction

 13i-12

correction

\frac{7-6i}{5}

correction

\frac{\sqrt{2}}{2}i

correction

2i+3

correction

 Propriétés (opérations avec les conjugués )

Soit z et z’ deux nombres complexes. 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

Exercice n°9

Déterminer les conjugués des nombres complexes suivants en fonction de \overline{z}.

 3z

correction

2iz

correction

z+1-2i

correction

\frac{z+1}{3}

correction

\frac{z+1}{z-i}

correction

z^2+2z

correction

\frac{z-i}{z+i}

correction

3z+5i

correction

 Propriétés du conjugué

Pour tout nombre complexe z. 

z+\overline{z}=2Re(z)

z-\overline{z}=2iIm(z)

z \in \mathbf{R}\iff z=\overline{z}

z  est imaginaire pur \iff z=-\overline{z}

Exercice n°10

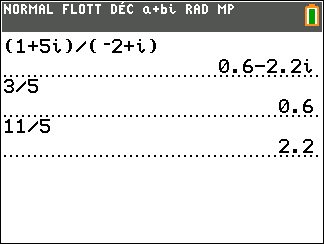
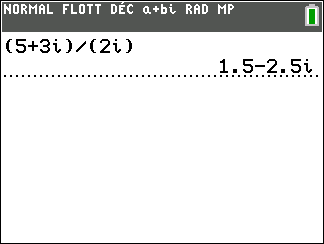
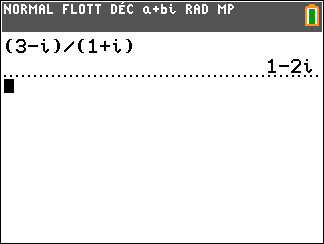
On considère z=\frac{3-i}{1+i}.

  1. Déterminer la forme algébrique de z.
correction

2. En utilisant les propriétés précédentes, en déduire les valeurs de z+\overline{z} et z-\overline{z}.

correction

Formule du binôme

Propriété : Formule du binôme de Newton

Soit a et b deux nombres complexes.

Pour tout entier naturel n, on a 

(a+b)^n=\sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}

Démonstration de la formule du binôme de Newton

On va montrer, par récurrence, que : pour tout entier naturel n, on a (a+b)^n=\sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}.

Initialisation : J’écris la propriété au premier rang en remplaçant tous les n par 0.

(a+b)^0=\sum\limits_{k=0}^{0}\binom{0}{k}a^0b^{0-k} est vraie car (a+b)^0=1 et \sum\limits_{k=0}^{0}\binom{0}{0}a^0b^0=1 .

Transmission ou hérédité:

(a+b)^n=\sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}\\(a+b)^{n+1}=(\sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k})(a+b)\\(a+b)^{n+1}=a\times \sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}+b\times \sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}\\(a+b)^{n+1}= \sum\limits_{k=0}^{n}\binom{n}{k}a^{k+1}b^{n-k}+ \sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k+1}\\(a+b)^{n+1}= \binom{n}{n}a^{n+1}b^{n-n}+\sum\limits_{k=0}^{n-1}\binom{n}{k}a^{k+1}b^{n-k}+ \binom{n}{0}a^{0}b^{n-0+1}+\sum\limits_{k=1}^{n}\binom{n}{k}a^{k}b^{n-k+1}\\(a+b)^{n+1}= a^{n+1}+\sum\limits_{k=0}^{n-1}\binom{n}{k}a^{k+1}b^{n-k}+ b^{n+1}+\sum\limits_{k=1}^{n}\binom{n}{k}a^{k}b^{n-k+1}\\(a+b)^{n+1}= a^{n+1}+\sum\limits_{k=1}^{n}\binom{n}{k-1}a^{k}b^{n-k+1}+ b^{n+1}+\sum\limits_{k=1}^{n}\binom{n}{k}a^{k}b^{n-k+1}\\(a+b)^{n+1}= a^{n+1}+b^{n+1}+\sum\limits_{k=1}^{n}(\binom{n}{k-1}+\binom{n}{k})a^{k} b^{n-k+1}\\(a+b)^{n+1}= a^{n+1}+b^{n+1}+\sum\limits_{k=1}^{n}\binom{n+1}{k}a^{k} b^{n-k+1}\\(a+b)^{n+1}=\binom{n+1}{n+1} a^{n+1}b^0+\binom{n+1}{0}a^0 b^{n+1}+\sum\limits_{k=1}^{n}\binom{n+1}{k}a^{k} b^{n-k+1}\\(a+b)^{n+1}=\sum\limits_{k=0}^{n+1}\binom{n+1}{k}a^k b^{n+1-k}

étape n°1 : j’écris la propriété au rang  n en haut.

étape n°3 : On muliplie l’égalité de l’étape n°1 par (a+b).

étape n°4 : On développe le produit de droite.

étape n°5 : On effectue les deux produits de droite.

étape n°6 : on remplace \sum\limits_{k=0}^{n}\binom{n}{k}a^{k+1}b^{n-k} par \binom{n}{n}a^{n+1}b^{n-n}+\sum\limits_{k=0}^{n-1}\binom{n}{k}a^{k+1}b^{n-k} et \sum\limits_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k+1} par \binom{n}{0}a^{0}b^{n-0+1}+\sum\limits_{k=1}^{n}\binom{n}{k}a^{k}b^{n-k+1}.

étape n°7 : on remplace \binom{n}{n} par 1 et \binom{n}{0} par 1.

étape n°8 : on remplace \sum\limits_{k=0}^{n-1}\binom{n}{k}a^{k+1}b^{n-k} par \sum\limits_{k=1}^{n}\binom{n}{k-1}a^{k}b^{n-k+1}

 

étape n°9 : on met a^{k}b^{n-k+1} en facteur dans \sum\limits_{k=1}^{n}\binom{n}{k}a^{k}b^{n-k+1}+ \sum\limits_{k=1}^{n}\binom{n}{k-1}a^{k}b^{n-k+1}

étape n°10 : on utilise la propriété \binom{n}{k-1}+\binom{n}{k}=\binom{n+1}{k}

étape n°11 : on remplace a^{n+1}  par \binom{n+1}{n+1} a^{n+1}b^0 et b^{n+1} par \binom{n+1}{0} a^{0}b^{n+1}.

étape n°2 : j’écris la propriété au rang n+1 en bas.

Conclusion

Donc pour tout entier naturel n, on a (a+b)^n=\sum\limits_{k=0}^{n}\binom{n}{k}a^kb^{n-k}

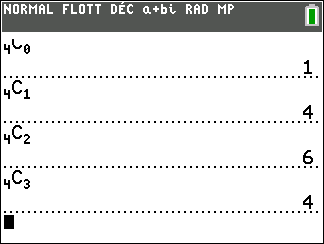
Exercice n°11

En utilisant la formule du binôme, déterminer la forme algébrique de (1+i)^4.

correction

©2020 – Math’O karé SAS

3+2i est la somme des deux termes : 3 et 2i ( on prend soin, si c’est nécessaire, d’écrire en deuxième le terme en i)

Le terme de la somme 3 est la partie réelle.

Dans le deuxième terme de la somme 2i, i est multiplié par 2, donc la partie imaginaire est 2.

Pour z=3+2i,

Re(z)=3 et Im(z)=2

-1+i est la somme des deux termes : -1 et i ( on prend soin, si c’est nécessaire, d’écrire en deuxième le terme en i)

Le terme de la somme -1 est la partie réelle.

Dans le deuxième terme de la somme i, i est multiplié par 1, donc la partie imaginaire est 1.

Pour z=-1+i,

Re(z)=-1 et Im(z)=1

-2i+6 est la somme des deux termes : 6 et -2i ( on prend soin, si c’est nécessaire, d’écrire en deuxième le terme en i)

Le terme de la somme 6 est la partie réelle.

Dans le deuxième terme de la somme -2i, i est multiplié par -2, donc la partie imaginaire est -2.

Pour z=-2i+6,

Re(z)=6 et Im(z)=-2

On peut imaginer que 9 est la somme des deux termes : 9 et 0 

Le terme de la somme 9 est la partie réelle.

Dans le deuxième terme de la somme 0, i est multiplié par 0, donc la partie imaginaire est 0.

Pour z=9,

Re(z)=9 et Im(z)=0

On peut imaginer que 4i est la somme des deux termes : 0 et 4i 

Le terme de la somme 0 est la partie réelle.

Dans le deuxième terme de la somme 4i, i est multiplié par 4, donc la partie imaginaire est 4.

Pour z=4i,

Re(z)=0 et Im(z)=4

On peut imaginer que -5i est la somme des deux termes : 0 et -5i 

Le terme de la somme 0 est la partie réelle.

Dans le deuxième terme de la somme -5i, i est multiplié par -5, donc la partie imaginaire est -5.

Pour z=-5i,

Re(z)=0 et Im(z)=-5

3i-2 est la somme des deux termes : -2 et 3i ( on prend soin, si c’est nécessaire, d’écrire en deuxième le terme en i)

Le terme de la somme -2 est la partie réelle.

Dans le deuxième terme de la somme 3i, i est multiplié par 3, donc la partie imaginaire est 3.

Pour z=3i-2,

Re(z)=-2 et Im(z)=3

On peut imaginer que i est la somme des deux termes : 0 et i ( on prend soin, si c’est nécessaire, d’écrire en deuxième le terme en i)

Le terme de la somme 0 est la partie réelle.

Dans le deuxième terme de la somme i, i est multiplié par 1, donc la partie imaginaire est 1.

Pour z=i,

Re(z)=0 et Im(z)=1

z.z’=(a+ib)(a’+ib’)

On développe

\hspace{0.6cm}=aa’+aib’+iba’+ibib’\\\hspace{0.6cm}=aa’+iab’+iba’+i^2bb’

On remplace i^2 par -1.

\hspace{0.6cm}=aa’+iab’+iba’-bb’\\\hspace{0.6cm}=aa’-bb’+i(ab’+ba’)

z_1=3-2i et z_2=-1+2i

On veut déterminer la forme algébrique de z_1+z_2.

z_1+z_2=3-2i-1+2i\\\hspace{1.15cm}=2

On vérifie avec la TI 83 Premium CE

z_1=3-2i et z_2=-1+2i

On veut déterminer la forme algébrique de 3z_1.

3z_1=3(3-2i)\\\hspace{0.6cm}=9-6i

On vérifie à l’aide de la calculatrice TI 83 Premium CE

z_1=3-2i et z_2=-1+2i

On veut déterminer la forme algébrique de z_1\times z_2.

z_1\times z_2=(3-2i)\times (-1+2i)

Plutôt que d’appliquer la formule, on préfère développer.

\hspace{1.15cm}=3\times(-1)+3\times(2i)-2i\times(-1)-2i\times2i\\\hspace{1.15cm}=-3+6i+2i-4i^2\\\hspace{1.15cm}=-3+8i-4\times(-1)\\\hspace{1.15cm}=-3+8i+4\\\hspace{1.15cm}=1+8i

On vérifie à l’aide de la calculatrice TI 83 Premium CE

z_1=3-2i et z_2=-1+2i

On veut déterminer la forme algébrique de z_1^2.

z_1^2=(3-2i)^2

On utilise l’identité remarquable (a-b)^2=a^2-2ab+b^2 avec a=3 et b=2i.

\hspace{0.5cm}=3^2-2\times3\times 2i+(2i)^2\\\hspace{0.5cm}=9-12i+4i^2\\\hspace{0.5cm}=9-12i-4\\\hspace{0.5cm}=5-12i

On vérifie avec la TI 83 Premium CE

z_1=\sqrt{2}+i et z_2=\sqrt{2}-i

On veut déterminer la forme algébrique de z_1+z_2.

z_1+z_2=\sqrt{2}+i+\sqrt{2}-i\\\hspace{1.15cm}=2\sqrt{2}

On vérifie avec la TI 83 Premium CE

z_1=\sqrt{2}+i et z_2=\sqrt{2}-i

On veut déterminer la forme algébrique de \sqrt{2}z_1.

\sqrt{2}z_1=\sqrt{2}(\sqrt{2}+i)\\\hspace{0.9cm}=\sqrt{2}^2+\sqrt{2}i\\\hspace{0.9cm}=2+\sqrt{2}i

On vérifie à l’aide de la calculatrice TI 83 Premium CE

z_1=\sqrt{2}+i et z_2=\sqrt{2}-i

On veut déterminer la forme algébrique de z_1\times z_2.

z_1\times z_2=(\sqrt{2}+i)\times (\sqrt{2}-i)

Plutôt que d’appliquer la formule, on préfère développer en utilisant l’identité remarquable

(a+b)(a-b)=a^2-b^2 avec a=\sqrt{2} et b=i.

\hspace{1.15cm}=\sqrt{2}^2-i^2\\\hspace{1.15cm}=2-(-1)\\\hspace{1.15cm}=2+1\\\hspace{1.15cm}=3

On vérifie à l’aide de la calculatrice TI 83 Premium CE

z_1=\sqrt{2}+i et z_2=\sqrt{2}-i

On veut déterminer la forme algébrique de z_1^2.

z_1^2=(\sqrt{2}+i)^2

On utilise l’identité remarquable (a+b)^2=a^2+2ab+b^2 avec a=\sqrt{2} et b=i.

\hspace{0.5cm}=\sqrt{2}^2+2\times\sqrt{2}\times i+i^2\\\hspace{0.5cm}=2+2\sqrt{2}i-1\\\hspace{0.5cm}=1+2\sqrt{2}i

On vérifie avec la TI 83 Premium CE

On veut résoudre l’équation 1+2i+z=2+i dans \mathbf{C}.

C’est une équations du premier degré, on doit remettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, 1+2i n’est pas à sa place, on enlève 1+2i de chaque côté.

z=2+i-1-2i\\z=1-i

L’ensemble solution est S=\{1-i\}

La solution correspond à ce qu’on a conjecturé précédemment avec Géogébra.

On veut résoudre l’équation 4+2z=3-i dans \mathbf{C}.

C’est une équations du premier degré, on doit remettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, 4 n’est pas à sa place, on enlève 4 de chaque côté.

2z=3-i-4\\2z=-1-i

Dans le membre de gauche, 2 n’est pas à sa place, on divise par 2 de chaque côté.

z=\frac{-1-i}{2}\\z=-\frac{1}{2}-\frac{1}{2}i

L’ensemble solution est S=\{-\frac{1}{2}-\frac{1}{2}i\}

La solution correspond à ce qu’on a conjecturé précédemment avec Géogébra.

On veut résoudre l’équation 2i-3z=3-i dans \mathbf{C}.

C’est une équation du premier degré, on doit remettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, 2i n’est pas à sa place, on enlève 2i de chaque côté.

-3z=3-i-2i\\-3z=3-3i

Dans le membre de gauche, -3 n’est pas à sa place, on divise par -3 de chaque côté.

z=\frac{3-3i}{-3}\\z=-1+i

L’ensemble solution est S=\{-1+i\}

La solution correspond à ce qu’on a conjecturé précédemment avec Géogébra.

On veut résoudre l’équation 3+i-2z=5+3i dans \mathbf{C}.

C’est une équation du premier degré, on doit remettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, 3+i n’est pas à sa place, on enlève 3+i de chaque côté.

-2z=5+3i-3-i\\-2z=2+2i

Dans le membre de gauche, -2 n’est pas à sa place, on divise par -2 de chaque côté.

z=\frac{2+2i}{-2}\\z=-1-i

L’ensemble solution est S=\{-1-i\}

La solution correspond à ce qu’on a conjecturé précédemment avec Géogébra.

Démonstration de la formule de l’inverse

Voici le début de la démonstration :

\frac{1}{z}=\frac{1}{a+ib}

On multiplie le second membre par  \frac{a-ib}{a-ib}

\hspace{0.6cm}=\frac{1}{a+ib}\times \frac{a-ib}{a-ib}\\\hspace{0.6cm}=\frac{a-ib}{(a+ib)(a-ib)}

On utilise une identité remarquable pour développer le produit au dénominateur (a-b)(a+b)=a^2-b^2.

\hspace{0.6cm}=\frac{a-ib}{a^2-(ib)^2}\\\hspace{0.6cm}=\frac{a-ib}{a^2-i^2b^2}

On remplace i^2 par -1

\hspace{0.6cm}=\frac{a-ib}{a^2-(-1)\times b^2}\\\hspace{0.6cm}=\frac{a-ib}{a^2+b^2}\\\hspace{0.6cm}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i

 

 

 

 On veut déterminer l’inverse de z=1+i.

On identifie la partie réelle de z : a=1 et la partie imaginaire de z : b=1.

On remplace a par 1 et b par 1 dans \frac{1}{z}=\frac{a}{a^2+b^2}+\frac{(-b)}{a^2+b^2}i

\frac{1}{z}=\frac{1}{1^2+1^2}+\frac{(-1)}{1^2+1^2}i

\frac{1}{z}=\frac{1}{2}-\frac{1}{2}i

On vérifie le résultat avec la TI 83 Premium CE

 On veut déterminer l’inverse de z=2-3i.

On identifie la partie réelle de z : a=2 et la partie imaginaire de z : b=-3.

On remplace a par 2 et b par -3 dans \frac{1}{z}=\frac{a}{a^2+b^2}+\frac{(-b)}{a^2+b^2}i

\frac{1}{z}=\frac{2}{2^2+(-3)^2}+\frac{(-(-3))}{2^2+(-3)^2}i

\frac{1}{z}=\frac{2}{13}+\frac{3}{13}i

On vérifie le résultat avec la TI 83 Premium CE. La calculatrice donne des valeurs décimales, on n’hésite pas à calculer \frac{2}{13} et \frac{3}{13}.

 On veut déterminer l’inverse de z=\sqrt{3}+i.

On identifie la partie réelle de z : a=\sqrt{3} et la partie imaginaire de z : b=1.

On remplace a par \sqrt{3} et b par 1 dans \frac{1}{z}=\frac{a}{a^2+b^2}+\frac{(-b)}{a^2+b^2}i

\frac{1}{z}=\frac{\sqrt{3}}{\sqrt{3}^2+1^2}+\frac{(-1)}{\sqrt{3}^2+1^2}i

\frac{1}{z}=\frac{\sqrt{3}}{4}-\frac{1}{4}i

On vérifie le résultat avec la TI 83 Premium CE. La calculatrice donne des valeurs décimales, on n’hésite pas à calculer \frac{\sqrt{3}}{4} et éventuellement \frac{1}{4}.

 On veut déterminer l’inverse de z=\sqrt{2}+i\sqrt{2}.

On identifie la partie réelle de z : a=\sqrt{2} et la partie imaginaire de z : b=\sqrt{2}.

On remplace a par \sqrt{2} et b par \sqrt{2} dans \frac{1}{z}=\frac{a}{a^2+b^2}+\frac{(-b)}{a^2+b^2}i

\frac{1}{z}=\frac{\sqrt{2}}{\sqrt{2}^2+\sqrt{2}^2}+\frac{-\sqrt{2}}{\sqrt{2}^2+\sqrt{2}^2}i

\frac{1}{z}=\frac{\sqrt{2}}{4}-\frac{\sqrt{2}}{4}i

On vérifie le résultat avec la TI 83 Premium CE. La calculatrice donne des valeurs décimales, on n’hésite pas à calculer \frac{\sqrt{2}}{4}.

 On veut mettre z_2=\frac{3-i}{1+2i} sous forme algébrique.

On va multiplier par le conjugué du dénominateur 1+2i c’est-à-dire 1-2i en haut et en bas.

z_2=\frac{3-i}{1+2i}\times \frac{1-2i}{1-2i} \\\hspace{0.42cm}=\frac{(3-i)(1-2i)}{(1+2i)(1-2i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.42cm}=\frac{3-6i-i+2i^2}{1^2-(2i)^2}\\\hspace{0.42cm}=\frac{3-6i-i+2\times(-1)}{1-4i^2}\\\hspace{0.42cm}=\frac{3-6i-i-2}{1-4\times(-1)}\\\hspace{0.42cm}=\frac{1-7i}{1+4}\\\hspace{0.42cm}=\frac{1-7i}{5}\\\hspace{0.42cm}=\frac{1}{5}-\frac{7}{5}i

On vérifie le résultat avec la TI 83 Premium CE. Comme la calculatrice donne des valeurs décimales, on peut éventuellement calculer \frac{1}{5} et \frac{7}{5}.

 On veut mettre z_3=\frac{\sqrt{2}+i}{\sqrt{2}-i} sous forme algébrique.

On va multiplier par le conjugué du dénominateur \sqrt{2}-i c’est-à-dire \sqrt{2}+i en haut et en bas.

z_3=\frac{\sqrt{2}+i}{\sqrt{2}-i}\times \frac{\sqrt{2}+i}{\sqrt{2}-i} \\\hspace{0.42cm}=\frac{(\sqrt{2}+i)(\sqrt{2}+i)}{(\sqrt{2}-i)(\sqrt{2}+i)}

On utilise l’identité remarquable (a+b)^2=a^2+2ab+b^2 pour développer le numérateur et on utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.42cm}=\frac{\sqrt{2}^2+2\sqrt{2}i+i^2}{\sqrt{2}^2-i^2}\\\hspace{0.42cm}=\frac{2+2\sqrt{2}i+(-1)}{2-(-1)}\\\hspace{0.42cm}=\frac{1+2\sqrt{2}i}{3}\\\hspace{0.42cm}=\frac{1}{3}+\frac{2\sqrt{2}}{3}i

On vérifie le résultat avec la TI 83 Premium CE. Comme la calculatrice donne des valeurs décimales, on peut éventuellement calculer \frac{1}{3} et \frac{2\sqrt{2}}{3}.

 On veut mettre z_4=\frac{1+5i}{-2+i} sous forme algébrique.

On va multiplier par le conjugué du dénominateur -2+i c’est-à-dire -2-i en haut et en bas.

z_4=\frac{1+5i}{-2+i}\times \frac{-2-i}{-2-i} \\\hspace{0.42cm}=\frac{(1+5i)(-2-i)}{(-2+i)(-2-i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.42cm}=\frac{-2-i-10i-5i^2}{(-2)^2-i^2}\\\hspace{0.42cm}=\frac{-2-i-10i-5\times(-1)}{4-(-1)}\\\hspace{0.42cm}=\frac{-2-i-10i+5}{4+1}\\\hspace{0.42cm}=\frac{3-11i}{5}\\\hspace{0.42cm}=\frac{3}{5}-\frac{11}{5}i

On vérifie le résultat avec la TI 83 Premium CE. Comme la calculatrice donne des valeurs décimales, on peut éventuellement calculer \frac{3}{5} et \frac{11}{5}.

 On veut mettre résoudre (1+i)z=2+i dans \mathbf{C}.

C’est une équation du premier degré. On va mettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, le facteur 1+i n’est pas à sa place, on divise par  1+i de chaque côté.

z=\frac{2+i}{1+i}

On va multiplier par le conjugué du dénominateur 1+i c’est-à-dire 1-i en haut et en bas.

\hspace{0.3cm}=\frac{2+i}{1+i}\times \frac{1-i}{1-i} \\\hspace{0.3cm}=\frac{(2+i)(1-i)}{(1+i)(1-i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.3cm}=\frac{2-2i+i-i^2}{1^2-i^2}\\\hspace{0.3cm}=\frac{2-2i+i-(-1)}{1-(-1)}\\\hspace{0.3cm}=\frac{2+-2i+i+1}{1+1}\\\hspace{0.3cm}=\frac{3-i}{2}\\\hspace{0.3cm}=\frac{3}{2}-\frac{1}{2}i

Donc S=\{\frac{3}{2}-\frac{1}{2}i\}

On peut vérifier que la forme algébrique est exacte avec la TI 83 Premium CE. 

 On veut résoudre iz=3-i dans \mathbf{C}.

C’est une équation du premier degré. On va mettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, le facteur i n’est pas à sa place, on divise par  i de chaque côté.

z=\frac{3-i}{i}

On va multiplier par le conjugué du dénominateur i c’est-à-dire -i en haut et en bas.

\hspace{0.3cm}=\frac{3-i}{i}\times \frac{-i}{-i} \\\hspace{0.3cm}=\frac{(3-i)(-i)}{(i)(-i)}\\\hspace{0.3cm}=\frac{-3i+i^2}{-i^2}\\\hspace{0.3cm}=\frac{-3i+(-1)}{-(-1)}\\\hspace{0.3cm}=\frac{-3i-1}{1}\\\hspace{0.3cm}=-3i-1\\\hspace{0.3cm}=-1-3i

Donc S=\{-1-3i\}

On peut vérifier que la forme algébrique est exacte avec la TI 83 Premium CE. 

 On veut  résoudre (1+2i)z=3-2i dans \mathbf{C}.

C’est une équation du premier degré. On va mettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, le facteur 1+2i n’est pas à sa place, on divise par  1+2i de chaque côté.

z=\frac{3-2i}{1+2i}

On va multiplier par le conjugué du dénominateur 1+2i c’est-à-dire 1-2i en haut et en bas.

\hspace{0.3cm}=\frac{3-2i}{1+2i}\times \frac{1-2i}{1-2i} \\\hspace{0.3cm}=\frac{(3-2i)(1-2i)}{(1+2i)(1-2i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.3cm}=\frac{3-6i-2i+(2i)^2}{1^2-(2i)^2}\\\hspace{0.3cm}=\frac{3-6i-2i+4i^2}{1-4i^2}\\\hspace{0.3cm}=\frac{3-6i-2i+4\times(-1)}{1-4\times(-1)}\\\hspace{0.3cm}=\frac{3-6i-2i-4}{1+4}\\\hspace{0.3cm}=\frac{-1-8i}{5}\\\hspace{0.3cm}=-\frac{1}{5}-\frac{8}{5}i

Donc S=\{-\frac{1}{5}-\frac{8}{5}i\}

On peut vérifier que la forme algébrique est exacte avec la TI 83 Premium CE. Comme la calculatrice donne des valeurs décimales, on peut éventuellement calculer \frac{1}{5} et \frac{8}{5}.

 On veut résoudre 2iz=5+3i dans \mathbf{C}.

C’est une équation du premier degré. On va mettre à leur place les membres qui ne sont pas à leur place.

Dans le membre de gauche, le facteur 2i n’est pas à sa place, on divise par  2i de chaque côté.

z=\frac{5+3i}{2i}

On va multiplier par le conjugué du dénominateur 2i c’est-à-dire -2i en haut et en bas.

\hspace{0.3cm}=\frac{5+3i}{2i}\times \frac{-2i}{-2i} \\\hspace{0.3cm}=\frac{(5+3i)(-2i)}{(2i)(-2i)}\\\hspace{0.3cm}=\frac{-10i-6i^2}{-4i^2}\\\hspace{0.3cm}=\frac{-10i-6\times(-1)}{-4\times(-1)}\\\hspace{0.3cm}=\frac{-10i+6}{4}\\\hspace{0.3cm}=-\frac{10}{4}i+\frac{6}{4}\\\hspace{0.3cm}=\frac{6}{4}-\frac{10}{4}i

On peut simplifier les fractions.

\hspace{0.3cm}=\frac{3}{2}-\frac{5}{2}i

Donc S=\{\frac{3}{2}-\frac{5}{2}i\}

On peut vérifier que la forme algébrique est exacte avec la TI 83 Premium CE. 

6-3i est la somme des deux termes : 6 et -3i.

Le terme de la somme 6 est la partie réelle.

Dans le deuxième terme de la somme -3i, i est multiplié par -3, donc la partie imaginaire est -3.

On remplace a par 6 et b par -3 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=6+3i

On peut vérifier le résultat avec la TI 83 Premium CE

2+i-\sqrt{2}=2-\sqrt{2}+i est la somme des deux termes : 2-\sqrt{2} et i ( on a pris soin d’écrire en dernier le terme en i)

Le terme de la somme 2-\sqrt{2} est la partie réelle.

Dans le deuxième terme de la somme i, i est multiplié par 1, donc la partie imaginaire est 1.

On remplace a par 2-\sqrt{2} et b par 1 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=2-\sqrt{2}-1i.

\hspace{0.25cm}=2-\sqrt{2}-i

On peut vérifier le résultat avec la TI 83 Premium CE.

2+i-\sqrt{2}=2-\sqrt{2}+i est la somme des deux termes : 2-\sqrt{2} et i ( on a pris soin d’écrire en dernier le terme en i)

Le terme de la somme 2-\sqrt{2} est la partie réelle.

Dans le deuxième terme de la somme i, i est multiplié par 1, donc la partie imaginaire est 1.

On remplace a par 2-\sqrt{2} et b par 1 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=2-\sqrt{2}-1i.

\hspace{0.25cm}=2-\sqrt{2}-i

-5i peut être la somme des deux termes : 0 et -5i.

Le terme de la somme 0 est la partie réelle.

Dans le deuxième terme de la somme -5i, i est multiplié par -5, donc la partie imaginaire est -5.

On remplace a par 0 et b par -5 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=0+5i\\\overline{z}=5i

On peut vérifier le résultat avec la TI 83 Premium CE

8 peut être la somme des deux termes : 8 et 0\times i.

Le terme de la somme 8 est la partie réelle.

Dans le deuxième terme de la somme 0\times i, i est multiplié par 0, donc la partie imaginaire est 0.

On remplace a par 8 et b par 0 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=8-0\times i\\\overline{z}=8

On peut vérifier le résultat avec la TI 83 Premium CE

13i-12=-12+13i est la somme des deux termes : -12 et 13i.

Le terme de la somme -12 est la partie réelle.

Dans le deuxième terme de la somme 13i, i est multiplié par 13, donc la partie imaginaire est 13.

On remplace a par -12 et b par 13 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=-12-13i

On peut vérifier le résultat avec la TI 83 Premium CE

\frac{7-6i}{5}=\frac{7}{5}-\frac{6}{5}i est la somme des deux termes : \frac{7}{5} et \frac{6}{5}i.

Le terme de la somme \frac{7}{5} est la partie réelle.

Dans le deuxième terme de la somme -\frac{6}{5}i, i est multiplié par -\frac{6}{5}, donc la partie imaginaire est -\frac{6}{5}.

On remplace a par \frac{7}{5} et b par -\frac{6}{5} dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=\frac{7}{5}+\frac{6}{5}i

On peut vérifier le résultat avec la TI 83 Premium CE

\frac{\sqrt{2}}{2}i peut être la somme des deux termes : 0 et \frac{\sqrt{2}}{2}i.

Le terme de la somme 0 est la partie réelle.

Dans le deuxième terme de la somme \frac{\sqrt{2}}{2}i, i est multiplié par \frac{\sqrt{2}}{2}, donc la partie imaginaire est \frac{\sqrt{2}}{2}.

On remplace a par 0 et b par \frac{\sqrt{2}}{2} dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=0-\frac{\sqrt{2}}{2}i\\\overline{z}=-\frac{\sqrt{2}}{2}i

On peut vérifier le résultat avec la TI 83 Premium CE

2i+3=3+2i est la somme des deux termes : 3 et 2i.

Le terme de la somme 3 est la partie réelle.

Dans le deuxième terme de la somme 2i, i est multiplié par 2, donc la partie imaginaire est 2.

On remplace a par 3 et b par 2 dans \overline{z}=a-ib

Le conjugué de z est

\overline{z}=3-2i

On peut vérifier le résultat avec la TI 83 Premium CE

Pour exprimer \overline{3z} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{3\times z}=\overline{3}\times \overline{z}

\overline{3\times z}=3 \overline{z}

Pour exprimer \overline{2iz} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{2i\times z}=\overline{2i}\times \overline{z}

\overline{2i\times z}=-2i \overline{z}

Pour exprimer \overline{z+1-2i} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{z+1-2i}=\overline{z}+ \overline{1-2i}

\overline{z+1-2i}=\overline{z}+ 1+2i

Pour exprimer \overline{(\frac{z+1}{3})} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{(\frac{z+1}{3})}=\frac{\overline{z+1}}{\overline{3}}

\overline{(\frac{z+1}{3})}=\frac{\overline{z}+1}{3}

Pour exprimer \overline{(\frac{z+1}{z-i})} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{(\frac{z+1}{z-i})}=\frac{\overline{z+1}}{\overline{z-i}}

\overline{(\frac{z+1}{z-i})}=\frac{\overline{z}+1}{\overline{z}+i}

Pour exprimer \overline{z^2+2z} en fonction de \overline{z},

on utilise \overline{z+z’}=\overline{z}+\overline{z’}

\overline{z^2+2z}=\overline{z^2}+\overline{2z}

Puis \overline{z\times z’}=\overline{z}\times \overline{z’} et \overline{z^n}=\overline{z}^n

\overline{z^2+2z}=\overline{z}^2+\overline{2}\times \overline{z}\\\overline{z^2+2z}=\overline{z}^2+2\overline{z}

Pour exprimer \overline{(\frac{z-i}{z-i})} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{(\frac{z-i}{z+i})}=\frac{\overline{z-i}}{\overline{z+i}}

\hspace{0.9cm}=\frac{\overline{z}-\overline{i}}{\overline{z}+\overline{i}}

\hspace{0.9cm}=\frac{\overline{z}-(-i)}{\overline{z}+(-i)}

\hspace{0.9cm}=\frac{\overline{z}+i}{\overline{z}-i}

Pour exprimer \overline{3z+5i} en fonction de \overline{z}, on utilise 

\overline{-z}=-\overline{z}

\overline{z+z’}=\overline{z}+\overline{z’}

\overline{z\times z’}=\overline{z}\times \overline{z’}

Pour tout entier n, \overline{z^n}=\overline{z}^n

Si z\neq 0, \overline{(\frac{1}{z})}=\frac{1}{\overline{z}}

Si z\neq 0, \overline{(\frac{z}{z’})}=\frac{\overline{z}}{\overline{z’}}

\overline{3z+5i}=\overline{3z}+ \overline{5i}

\hspace{1.2cm}=\overline{3}\times \overline{z}-5i

\hspace{1.2cm}=3 \overline{z}-5i

 On veut mettre z=\frac{3-i}{1+i} sous forme algébrique.

On va multiplier par le conjugué du dénominateur 1+i c’est-à-dire 1-i en haut et en bas.

z=\frac{3-i}{1+i}\times \frac{1-i}{1-i} \\\hspace{0.42cm}=\frac{(3-i)(1-i)}{(1+i)(1-i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

\hspace{0.42cm}=\frac{3-3i-i+i^2}{1^2-i^2}\\\hspace{0.42cm}=\frac{3-3i-i-1}{1-(-1)}\\\hspace{0.42cm}=\frac{2-4i}{2}\\\hspace{0.42cm}=1-2i

On vérifie le résultat avec la TI 83 Premium CE. 

On utilise les résultat du cours 

z+\overline{z}=2Re(z)

z-\overline{z}=2iIm(z).

Comme z=1-2i , Re(z)=1 et Im(z)=-2.

Donc z+\overline{z}=2\times{1}=2 et z-\overline{z}=2i\times{-2}=-4i.

 

(1+i)^4=\sum\limits_{k=0}^{4}\binom{4}{k}1^k\times i^{4-k}\\\hspace{1.3cm}=\binom{4}{0}1^0\times i^{4-0}+\binom{4}{1}1^1\times i^{4-1}+\binom{4}{2}1^2\times i^{4-2}+\binom{4}{3}1^3\times i^{4-3}+\binom{4}{4}1^4\times i^{4-4}

On peut déterminer \binom{4}{0} , \binom{4}{1} , \binom{4}{2} , … avec la calculatrice

\hspace{1.3cm}=1\times1\times i^4+4\times1\times i^3+6\times1\times i^{2}+4\times1\times i^1+1\times1\times i^0\\\hspace{1.3cm}= i^4+4i^3+6i^{2}+4 i^1+i^0\\\hspace{1.3cm}= i^2\times i^2+4i\times i^2+6i^{2}+4 i^1+i^0\\\hspace{1.3cm}= (-1)\times(-1)+4i\times(-1)+6\times(-1)+4 i+1\\\hspace{1.3cm}= 1-4i-6+4 i+1\\\hspace{1.3cm}= -4

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.