TE. Complexes et géométrie : affixe d’un point, affixe d’un vecteur.

Complexes et géométrie, Niveau maths expertes, Nombres complexes

Définition : affixe d’un point et point image.

A tout point $M$ du plan de coordonnées $(x;y)$ est associé le complexe $z=x+iy$ appelé affixe du point $M$ .

A tout nombre complexe $z=x+iy$ , on associe le point $M$ de coordonnées $(x;y)$ .

Le plan muni d’un repère orthonormal direct dans lequel on représente des nombres complexes est appelé plan complexe

Exercice n°1

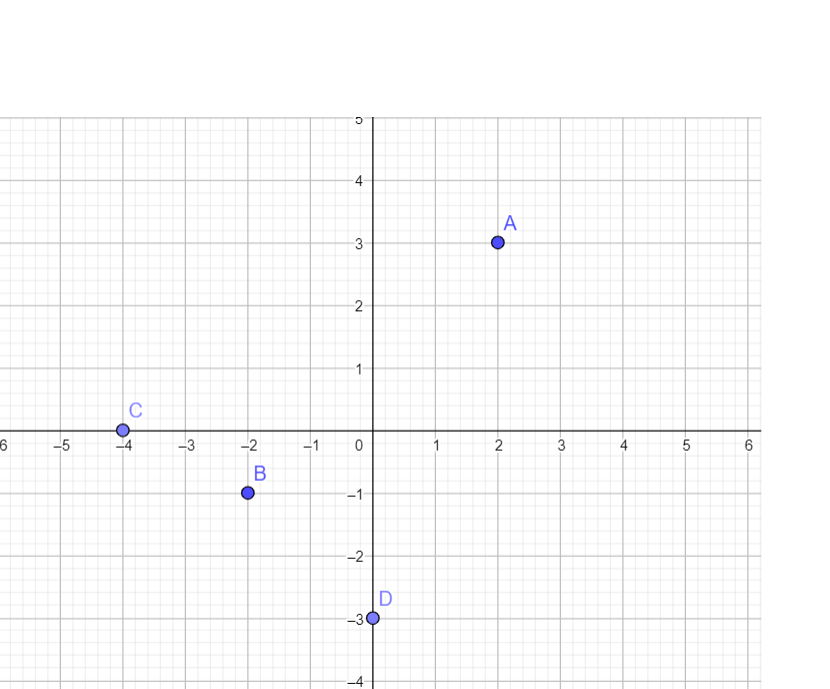
En utilisant la page Géogébra ci-dessus, placer les points suivants :

$A$ d’affixe $z_A=2+3i$ , $B$ d’affixe $z_B=-2-i$ , $C$ d’affixe $z_C=-4$ et $D$ d’affixe $z_D=-3i$ .

Exercice n°2

En utilisant la page Géogébra ci-dessus, placer les points suivants :

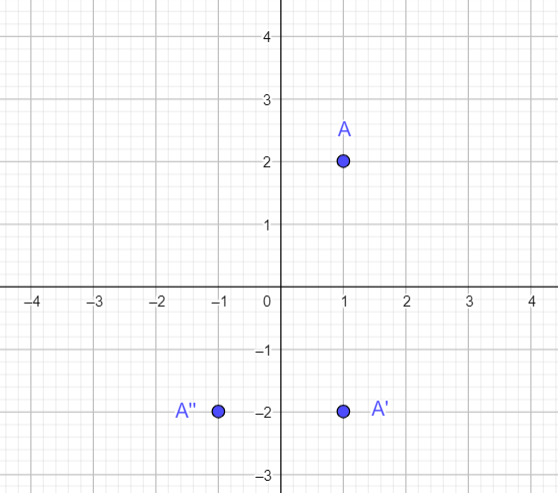
$A$ d’affixe $z_A=1+2i$ , $A’$ d’affixe $z_A’=\overline{z_A}$ et $A"$ d’affixe $z_A"=-z_A$

2. a. Par quelle transformation géométrique, obtient-on $A’$ à partir de $A$ ?

2. b. Par quelle transformation géométrique, obtient-on $A"$ à partir de $A$ ?

Propriété

Soit $M$ un point du plan d’affixe $z$ , alors

$-z$ est l’affixe du symétrique du point $M$ par rapport à l’origine
$\overline{z}$ est l’affixe du symétrique du point $M$ par rapport à l’axe des abscisses

Exemple : voir exercice n°2

Théorème : égalité de deux points

Soit $A(z_A)$ et $B(z_B)$ deux points du plan complexe.

$A=B \iff z_A=z_B$ .

Théorème : affixe du milieu du segment [AB]

Soit $A(z_A)$ et $B(z_B)$ deux points du plan complexe.

Le milieu de $[AB]$ a pour affixe $\frac{z_A+z_B}{2}$ .

Exercice n°3

En utilisant la page Géogébra ci-dessus, placer les points suivants :

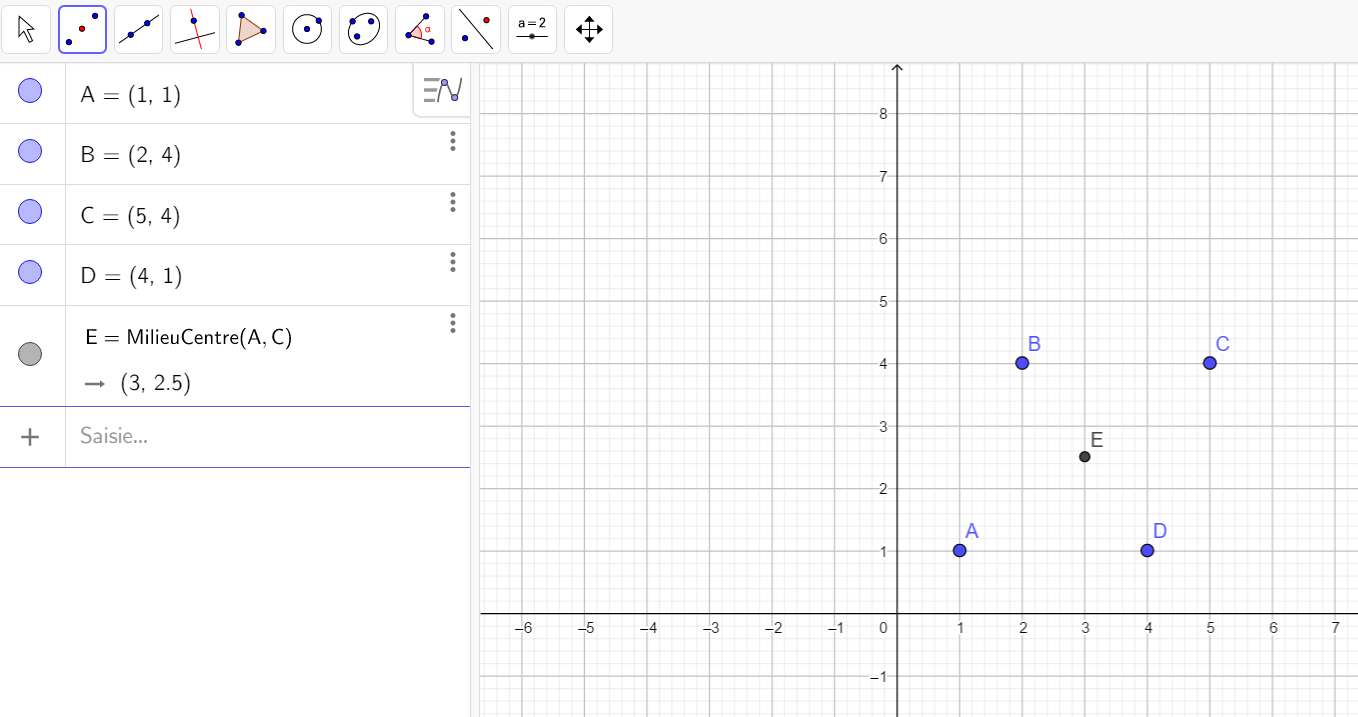
$A(z_A=1+i)$ , $B(z_B=2+4i)$ , $C(z_C=5+4i)$ et $D(z_D=4+i)$ .

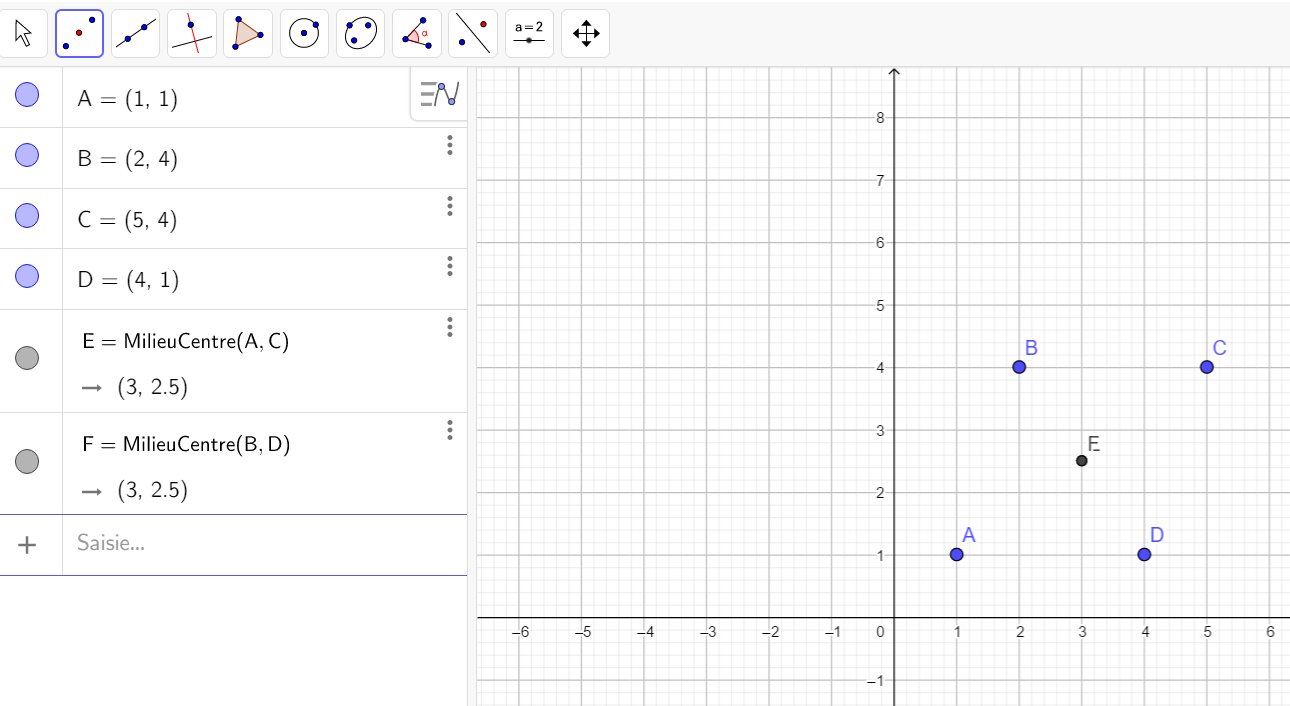
2. a. Calculer l’affixe du milieu de $[AC]$ .

2. b. Calculer l’affixe du milieu de $[BD]$ .

2. c. En déduire la nature du quadrilatère $ABCD$ .

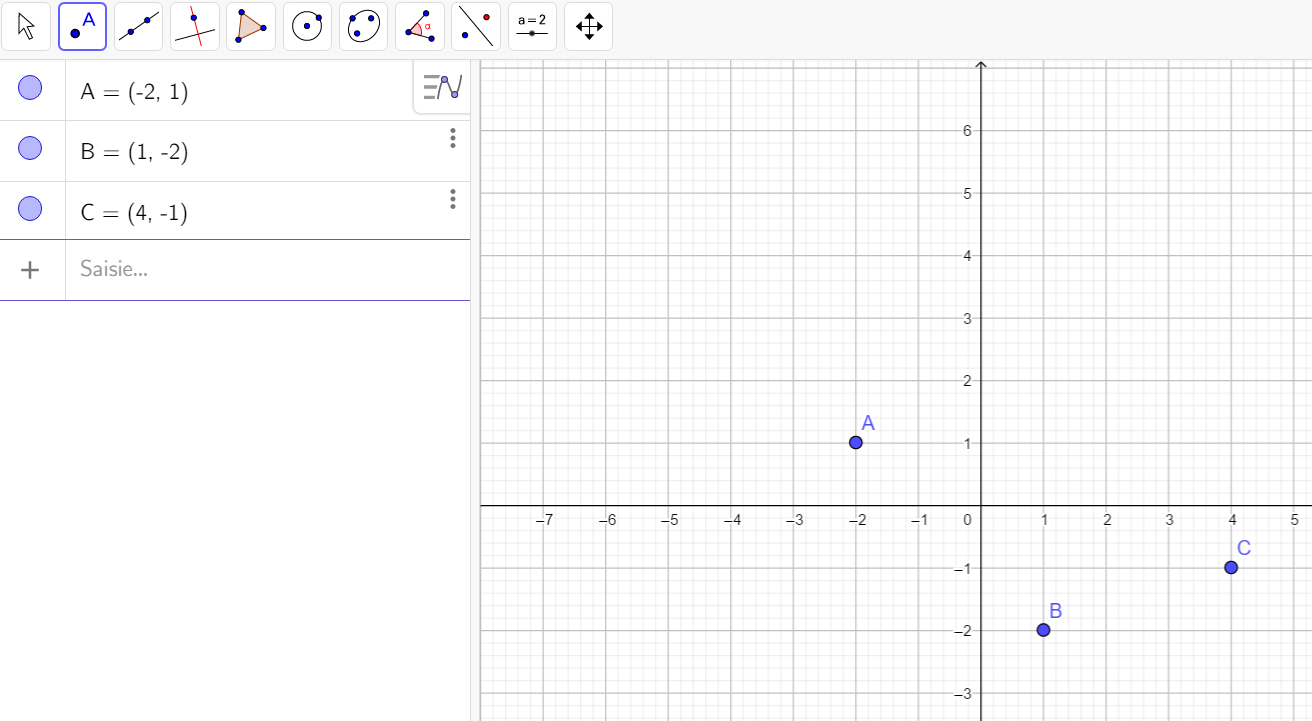
Exercice n°4

En utilisant la page Géogébra ci-dessus, placer les points suivants :

$A(z_A=-2+i)$ , $B(z_B=1-2i)$ , $C(z_C=4-i)$ .

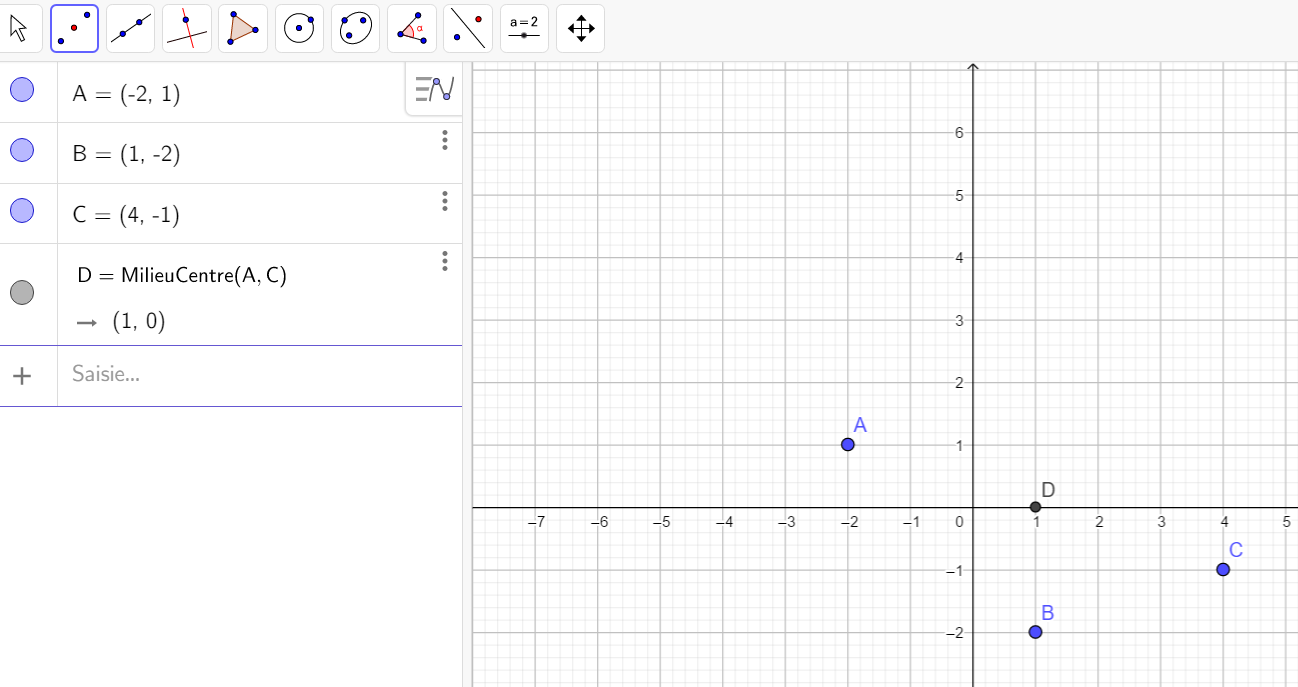
2. a. Calculer l’affixe du milieu de $[AC]$ .

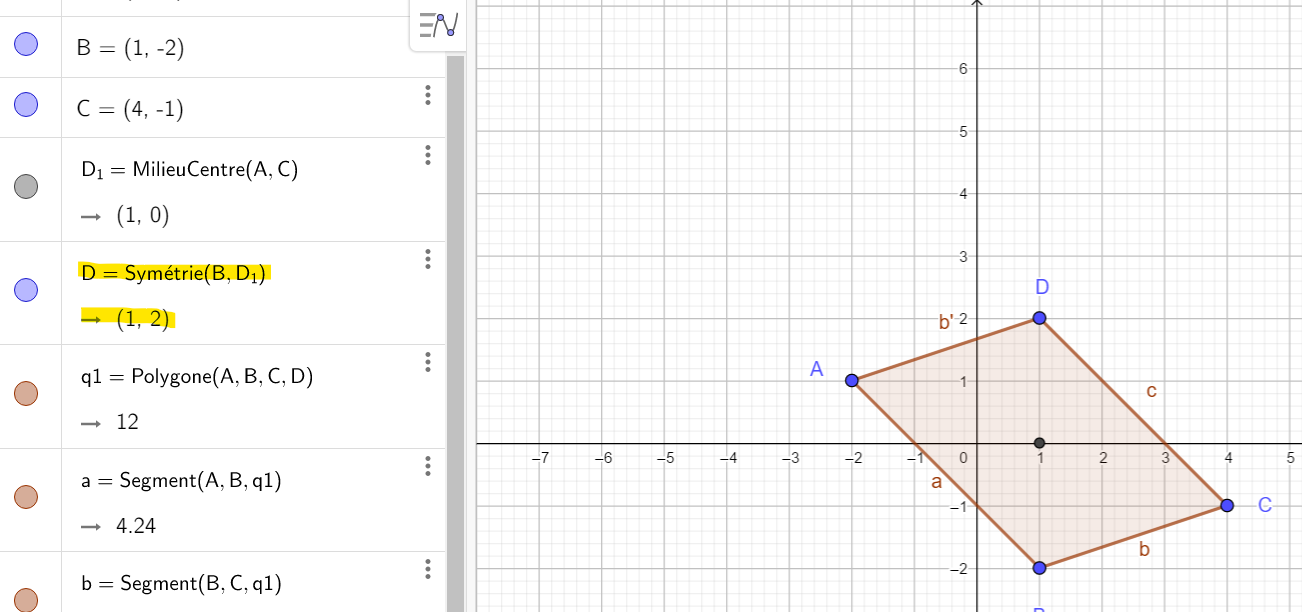
2. b. On considère le point $D$ qui est le quatrième sommet du parallélogramme $ABCD$ . On note $x+iy$ l’affixe du point de $D$ . Exprimer l’affixe du milieu de $[BD]$ en fonction de $x$ et de $y$ .

2. c. En déduire, par le calcul, l’affixe du point $D$ .

Définition : affixe d’un vecteur

A tout vecteur $\overrightarrow{v}$ du plan de coordonnées $(a;b)$ est associé le complexe $z=a+ib$ appelé affixe du vecteur $\overrightarrow{v}$ .

Théorème : égalité de deux vecteurs

Soit $\overrightarrow{v_1}(z_{\overrightarrow{v_1}})$ et $\overrightarrow{v_2}(z_{\overrightarrow{v_2}})$ deux vecteurs du plan complexe.

$\overrightarrow{v_1}=\overrightarrow{v_2} \iff z_{\overrightarrow{v_1}}=z_{\overrightarrow{v_2}}$ .

Théorème : affixe d’un vecteur

Soit $A(z_A)$ et $B(z_B)$ deux points du plan complexe.

$\overrightarrow{AB}$ a pour affixe $z_{\overrightarrow{AB}}=z_B-z_A$ .

Exemple :

Soit $A(z_A)$ et $B(z_B)$ alors $\overrightarrow{AB}$ a pour affixe $z_{\overrightarrow{AB}}=z_B-z_A$ .

Soit $A(2-3i)$ et $B(6+i)$ alors $\overrightarrow{AB}$ a pour affixe $z_{\overrightarrow{AB}}=(6+i)-(2-3i)$ .

\hspace{7.52cm}=6+i-2+3i\\\hspace{7.52cm}=4+4i

Exercice n°5

Soient $A(z_A=-1+2i)$ , $B(z_B=1+3i)$ , $C(z_C=5)$ .

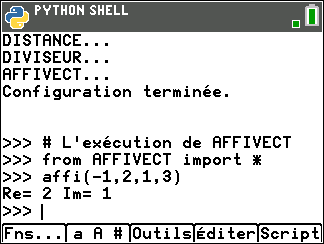
Calculer les affixes des vecteurs suivants. On pourra vérifier le résultat en utilisant le programme en Python que vous trouverez dans l’article : TE. Programmer sa TI 83 Edition PYTHON en langage Python : calculer l’affixe d’un vecteur.

\overrightarrow{AB}

\overrightarrow{BC}

\overrightarrow{AC}

\overrightarrow{BA}

Exercice n°6

Soient $A(z_A=-3+3i)$ , $B(z_B=4i)$ , $C(z_C=2+2i)$ et $D(z_D=-1+i)$ .

Déterminer l’affixe du vecteur $\overrightarrow{AB}$ .

2. Déterminer l’affixe du vecteur $\overrightarrow{DC}$ .

3. En déduire la nature du quadrilatère $ABCD$ .

Exercice n°7

Soient $A(z_A=-1+3i)$ , $B(z_B=4+5i)$ , $C(z_C=6+3i)$ .

On veut déterminer l’affixe du point $D$ pour que le quadrilatère $ABCD$ soit un parallélogramme.

Comme on ne la connaît pas, on notera $x+iy$ l’affixe du point $D$ .

Déterminer l’affixe du vecteur $\overrightarrow{AB}$ .

2. Exprimer l’affixe du vecteur $\overrightarrow{DC}$ en fonction de $x$ et de $y$ .

3. En utilisant le fait que $\overrightarrow{AB}=\overrightarrow{DC}$ en déduire les valeurs de $x$ et de $y$ . Conclure.

Théorème : opérations et affixe d’un vecteur.

Soit $\overrightarrow{u_1}(z_1)$ et $\overrightarrow{u_2}(z_2)$ deux vecteurs.

$\overrightarrow{u_1}+\overrightarrow{u_2}$ a pour affixe $z_1+z_2$

$\overrightarrow{u_1}-\overrightarrow{u_2}$ a pour affixe $z_1-z_2$

$-\overrightarrow{u_1}$ a pour affixe $-z_1$

$k\overrightarrow{u_1}$ a pour affixe $kz_1$

Exercice n°8

Soient $A(z_A=2-i)$ , $B(z_B=3+3i)$ .

Le but de l’exercice est de déterminer l’affixe du point $C$ défini par $\overrightarrow{AC}=4\overrightarrow{AB}$ .

Comme on ne la connaît pas, on notera $x+iy$ l’affixe du point $C$ .

Déterminer l’affixe du vecteur $\overrightarrow{AB}$ . Puis celle de $4\overrightarrow{AB}$

2. Exprimer l’affixe du vecteur $\overrightarrow{AC}$ en fonction de $x$ et de $y$ .

3. déduire des questions précédentes l’affixe du point $C$ .

Exercice n°9

Soient $A(z_A=3-3i)$ , $B(z_B=6-i)$ et $C(z_C=-2+2i)$ .

Le but de l’exercice est de déterminer l’affixe du point $D$ défini par $\overrightarrow{AD}=2\overrightarrow{AB}-\overrightarrow{AC}$ soit un parallélogramme.

Comme on ne la connaît pas, on notera $x+iy$ l’affixe du point $D$ .

1.a.Déterminer l’affixe du vecteur $\overrightarrow{AB}$ . Puis celle de $2\overrightarrow{AB}$