logo

TE. Complexes et géométrie : module d’un nombre complexe.

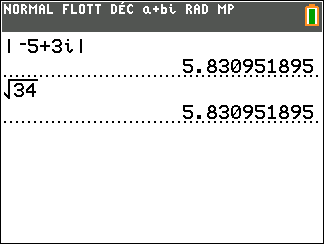
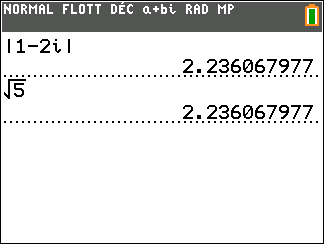
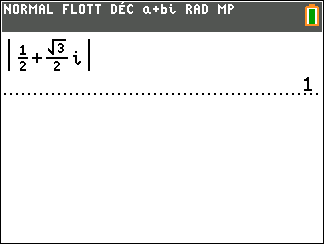
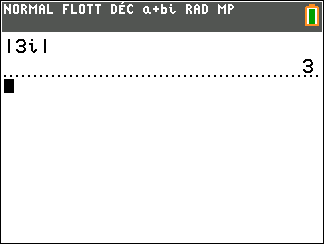
Définition du module d’un complexe

z est un nombre de forme algébrique a+ib avec a\in \mathbf{R} et b\in \mathbf{R}.

Le module de z est le nombre réel positif noté |z| défini par |z|=\sqrt{a^2+b^2}

Exemple 

Calculons le module du nombre complexe  z=-3+4i

On remplace a par la partie rélle de z qui vaut -3 et b par la partie imaginaire de z qui vaut 4 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-3)^2+4^2}

\hspace{0.5cm}=\sqrt{9+16}

\hspace{0.5cm}=\sqrt{25}

\hspace{0.5cm}=5

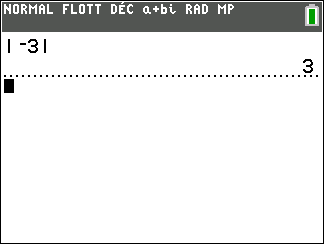
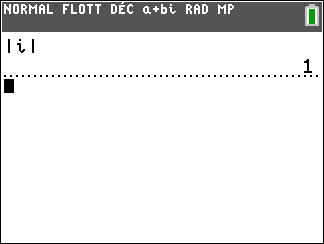
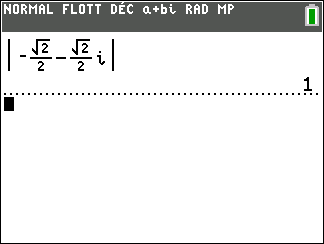
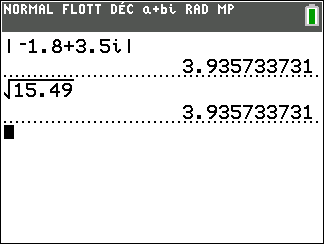
Méthode pour calculer le module d’un complexe avec la TI 83 premium CE.

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

Sur la 5ème ligne sélectionner abs( , puis saisir à la suite le nombre complexe.

Exemple : déterminons le module du complexe -3+4i

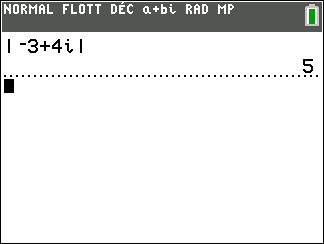
Exercice n°1

Calculer le module du nombre complexe dans chaque cas z=-3+4i

z_1=-5+3i

correction
je valide avec ma TI

z_2=1-2i

correction
je valide avec ma TI

z_3=\frac{1}{2}+\frac{\sqrt{3}}{2}i

correction
je valide avec ma TI

z_4=3i

correction
je valide avec ma TI

z_5=-3

correction
je valide avec ma TI

z_6=i

correction
je valide avec ma TI

z_7=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i

correction
je valide avec ma TI

z_8=-1.8+3.5i

correction
je valide avec ma TI

Propriétés du module d’un complexe

z est un nombre complexe.

|z|=0 \iff z=0

|-z|=|z|

|\overline{z}|=|z|

z\times\overline{z}=|z|^2

Démonstration de la quatrième propriété

On va montrer que z\times\overline{z} et |z|^2 sont tous les deux égaux à une même troisième quantité.

On pose z=a+ib .

z\times\overline{z}=(a+ib)(a-ib) \\z\times\overline{z}=a^2-(ib)^2 \\z\times\overline{z}=a^2-i^2\times b^2\\z\times\overline{z}=a^2-(-1)\times b^2\\z\times\overline{z}=a^2+ b^2
|z|^2=(\sqrt{a^2+b^2})^2\\|z|^2=a^2+b^2

 

Donc z\times\overline{z}=|z|^2

Théorème : module et opérations

 Soient z et z’ deux nombres complexes.

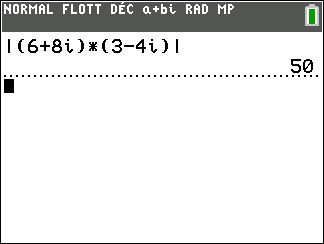
|z\times z’|=|z|\times| z’|

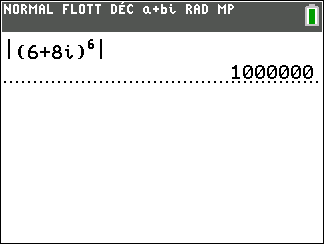
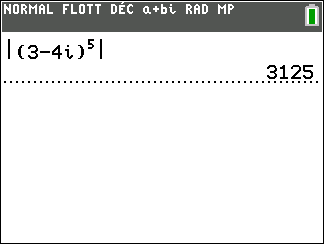
|z^n|=|z|^n

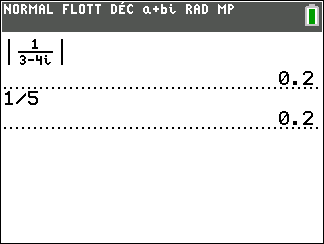
|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

Exercice n°2

z_1=6+8i et z_2=3-4i

  1. Calculer |z_1| et |z_2|
correction de |z_1|
correction de |z_2|
je valide avec ma TI

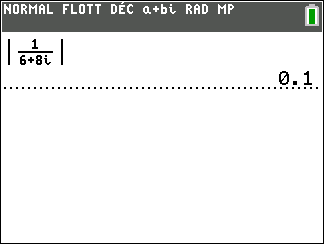
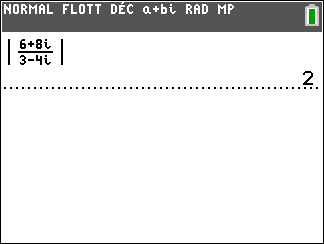
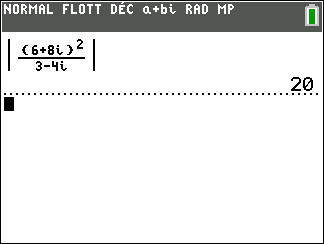
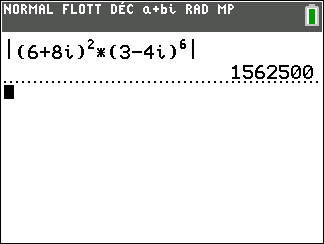
2. En utilisant les propriétés précédentes, calculer 

|(6+8i)(3-4i)

correction
je valide avec ma TI

|(6+8i)^6|

correction
je valide avec ma TI

|(3-4i)^5|

correction
je valide avec ma TI

|\frac{1}{3-4i}|

correction
je valide avec ma TI

|\frac{1}{6+8i}|

correction
je valide avec ma TI

|\frac{6+8i}{3-4i}|

correction
je valide avec ma TI

|\frac{(6+8i)^2}{3-4i}|

correction
je valide avec ma TI

|(6+8i)^2(3-4i)^6|

correction
je valide avec ma TI

Théorème : module et distance

 Soient A(z_A) et B(z_B), on a AB=|z_B-z_A|.

Exercice n°3

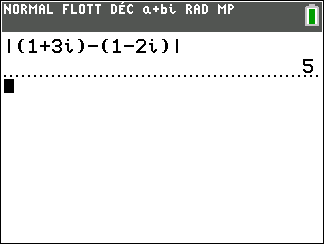
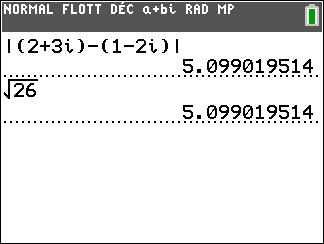
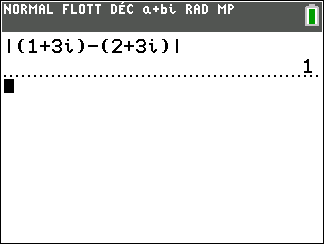
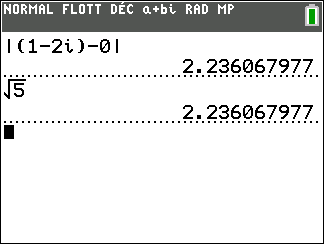
Calculer les distances suivantes

AB avec z_A=1-2i et z_B=1+3i

correction
je valide avec ma TI

AC avec z_A=1-2i et z_C=2+3i

correction
je valide avec ma TI

CB avec z_C=2+3i et z_B=1+3i

correction
je valide avec ma TI

OA avec z_O=0 et z_A=1-2i

correction
je valide avec ma TI

Exercice n°4

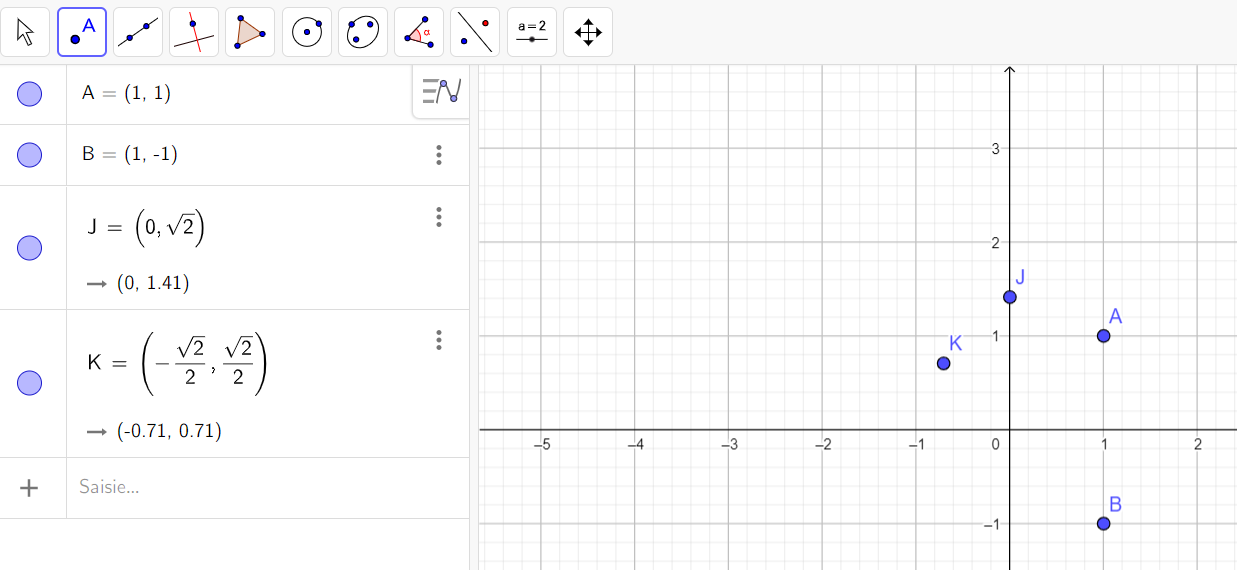
Dans un repère orthonormé (O,\overrightarrow{u},\overrightarrow{v}), on donne z_A=1+i , z_B=1-i , z_J=i\sqrt{2} et z_K=-\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}.

  1. Placer les points A,B,J et K dans le repère de la fenêtre Géogébra ci-dessous.

Pour placer le point J, saisir dans la colonne de gauche :

J=(0,\sqrt{2}) et faire entrer.

Pour saisir \sqrt{2}, cliquer sur le petit clavier situé en bas de l’écran qui apparaît quand on commence à saisir la formule. 

correction

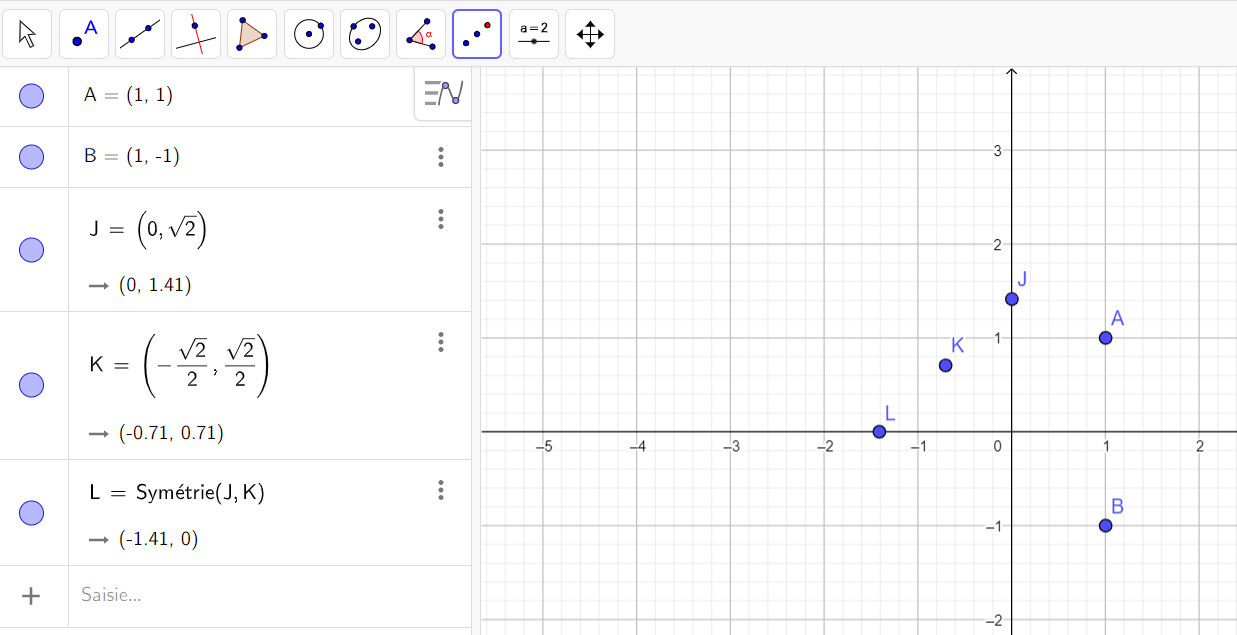
2. Soit L le symétrique du point J par rapport au point K. Déterminer z_L l’affixe du point L.

correction

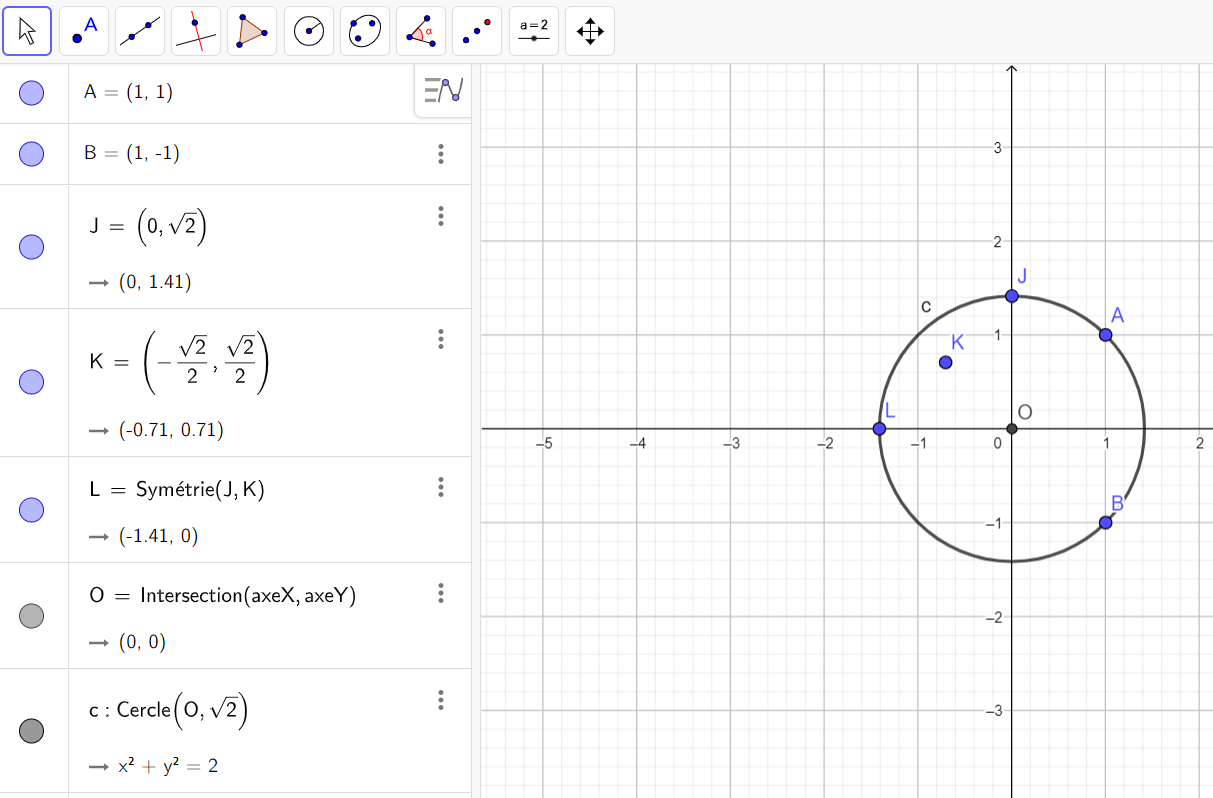
3. Montrer que les points A, B, J et L appartiennent au cercle de O er de rayon \sqrt{2}.

correction

Exercice n°5

Dans un repère orthonormé, on donne z_A=5+i et z_B=6+5i.

1.Déterminer l’ensemble des points M d’affixe z qui vérifient |z-5-i|=2

correction

2.Déterminer l’ensemble des points M d’affixe z qui vérifient |z-5-i|=|z-6-5i|

correction

Exercice n°6

Dans un repère orthonormé, on donne z_C=6-i et z_D=-5+2i.

1.Déterminer l’ensemble des points M d’affixe z qui vérifient |z+5-2i|=4

correction

2.Déterminer l’ensemble des points M d’affixe z qui vérifient |z+5-2i|=|z-6+i|

correction

©2020 – Math’O karé SAS

Calculons le module du nombre complexe  z_1=-5+3i

On remplace a par la partie rélle de z_1 qui vaut -5 et b par la partie imaginaire de z_1 qui vaut 3 dans 

|z|=\sqrt{a^2+b^2}.

|z_1|=\sqrt{(-5)^2+3^2}

\hspace{0.5cm}=\sqrt{25+9}

\hspace{0.5cm}=\sqrt{34}

Calculons le module du nombre complexe  z_2=1-2i

On remplace a par la partie rélle de z_2 qui vaut 1 et b par la partie imaginaire de z_2 qui vaut -2 dans 

|z|=\sqrt{a^2+b^2}.

|z_2|=\sqrt{1^2+(-2)^2}

\hspace{0.5cm}=\sqrt{1+4}

\hspace{0.5cm}=\sqrt{5}

Calculons le module du nombre complexe  z_3=\frac{1}{2}+\frac{\sqrt{3}}{2}i

On remplace a par la partie rélle de z_3 qui vaut \frac{1}{2} et b par la partie imaginaire de z_3 qui vaut \frac{\sqrt{3}}{2} dans 

|z|=\sqrt{a^2+b^2}.

|z_3|=\sqrt{(\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}

\hspace{0.6cm}=\sqrt{\frac{1^2}{2^2}+\frac{\sqrt{3}^2}{2^2}}

\hspace{0.6cm}=\sqrt{\frac{1}{4}+\frac{3}{4}}

\hspace{0.6cm}=\sqrt{\frac{4}{4}}

\hspace{0.6cm}=\sqrt{1}

\hspace{0.6cm}=1

 

Calculons le module du nombre complexe  z_4=3i

On remplace a par la partie rélle de z_4 qui vaut 0 et b par la partie imaginaire de z_4 qui vaut 3 dans 

|z|=\sqrt{a^2+b^2}.

|z_4|=\sqrt{0^2+3^2}

\hspace{0.6cm}=\sqrt{0+9}

\hspace{0.6cm}=\sqrt{9}

\hspace{0.6cm}=3

Calculons le module du nombre complexe  z_5=-3

On remplace a par la partie rélle de z_5 qui vaut -3 et b par la partie imaginaire de z_5 qui vaut 0 dans 

|z|=\sqrt{a^2+b^2}.

|z_5|=\sqrt{(-3)^2+0^2}

\hspace{0.6cm}=\sqrt{9+0}

\hspace{0.6cm}=\sqrt{9}

\hspace{0.6cm}=3

Calculons le module du nombre complexe  z_6=i

On remplace a par la partie rélle de z_6 qui vaut 0 et b par la partie imaginaire de z_6 qui vaut 1 dans 

|z|=\sqrt{a^2+b^2}.

|z_6|=\sqrt{0^2+1^2}

\hspace{0.6cm}=\sqrt{0+1}

\hspace{0.6cm}=\sqrt{1}

\hspace{0.6cm}=1

Calculons le module du nombre complexe  z_7=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i

On remplace a par la partie rélle de z_7 qui vaut -\frac{\sqrt{2}}{2} et b par la partie imaginaire de z_7 qui vaut -\frac{\sqrt{2}}{2} dans 

|z|=\sqrt{a^2+b^2}.

|z_7|=\sqrt{(\frac{(-\sqrt{2})}{2})^2+(\frac{(-\sqrt{2})}{2})^2}

\hspace{0.6cm}=\sqrt{\frac{\sqrt{2}^2}{2^2}+\frac{\sqrt{2}^2}{2^2}}

\hspace{0.6cm}=\sqrt{\frac{2}{4}+\frac{2}{4}}

\hspace{0.6cm}=\sqrt{\frac{4}{4}}

\hspace{0.6cm}=\sqrt{1}

\hspace{0.6cm}=1

Calculons le module du nombre complexe  z_8=-1.8+3.5i

On remplace a par la partie rélle de z_8 qui vaut -1.8 et b par la partie imaginaire de z_8 qui vaut 3.5 dans 

|z|=\sqrt{a^2+b^2}.

|z_8|=\sqrt{(-1.8)^2+3.5^2}

\hspace{0.5cm}=\sqrt{3.24+12.25}

\hspace{0.5cm}=\sqrt{15.49}

Calculons le module du nombre complexe  z_1=6+8i

On remplace a par la partie rélle de z_1 qui vaut 6 et b par la partie imaginaire de z_1 qui vaut 8 dans 

|z|=\sqrt{a^2+b^2}.

|z_1|=\sqrt{6^2+8^2}

\hspace{0.6cm}=\sqrt{36+64}

\hspace{0.6cm}=\sqrt{100}

\hspace{0.6cm}=10

Calculons le module du nombre complexe  z_2=3-4i

On remplace a par la partie rélle de z_2 qui vaut 3 et b par la partie imaginaire de z_2 qui vaut -4 dans 

|z|=\sqrt{a^2+b^2}.

|z_2|=\sqrt{3^2+(-4)^2}

\hspace{0.6cm}=\sqrt{9+16}

\hspace{0.6cm}=\sqrt{25}

\hspace{0.6cm}=5

Pour calculer |(6+8i)(3-4i)| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|(6+8i)(3-4i)|=|6+8i||3-4i|\\\hspace{2.65cm}=10\times 5\\\hspace{2.65cm}=50

Pour calculer |(6+8i)^6| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|(6+8i)^6|=|6+8i|^6\\\hspace{1.6cm}=10^6\\\hspace{1.6cm}=1000000

Pour calculer |(3-4i)^5| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|(3-4i)^5|=|3-4i|^5\\\hspace{1.6cm}=5^5\\\hspace{1.6cm}=3125

Pour calculer |\frac{1}{3-4i}| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|\frac{1}{3-4i}|=\frac{1}{|3-4i|}\\\hspace{0.9cm}=\frac{1}{5}

 

Pour calculer |\frac{1}{6+8i}| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|\frac{1}{6+8i}|=\frac{1}{|6+8i|}\\\hspace{0.9cm}=\frac{1}{10}

Pour calculer |\frac{6+8i}{3-4i}| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|\frac{6+8i}{3-4i}|=\frac{|6+8i|}{|3-4i|}\\\hspace{0.9cm}=\frac{10}{5}\\\hspace{0.9cm}=2

Pour calculer |\frac{(6+8i)^2}{3-4i}| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|\frac{(6+8i)^2}{3-4i}|=\frac{|6+8i|^2}{|3-4i|}\\\hspace{0.9cm}=\frac{10^2}{5}\\\hspace{0.9cm}=\frac{100}{5}\\\hspace{0.9cm}=20

Pour calculer |(6+8i)^2(3-4i)^6| , on utilise : 

|z\times z’|=|z|\times| z’|

|z^n|=|z|^n

|\frac{1}{z}|=\frac{1}{|z|} et |\frac{z’}{z}|=\frac{|z’|}{|z|} , si z\ne 0

|z+z’|\leq |z|+|z’|

|(6+8i)^2(3-4i)^6|=|6+8i|^2|3-4i|^6\\\hspace{2.95cm}=10^2\times 5^6\\\hspace{2.95cm}=100\times 15625\\\hspace{2.95cm}=1562500

A(z_A=1-2i) et B(z_B=1+3i) 

Pour calculer la distance AB , on remplace z_A par 1-2i et z_B par 1+3i dans 

AB=|z_B-z_A|.

AB=|(1+3i)-(1-2i)|

\hspace{0.66cm}=|1+3i-1+2i|

\hspace{0.66cm}=|0+5i|

\hspace{0.66cm}=|5i|

méthode n°1 : Pour calculer |5i|, on peut utiliser les propriétés du module

\hspace{0.66cm}=|5|\times|i|=5\times1=5

méthode n°2 : Pour calculer |5i|, on peut utiliser la définition

\hspace{0.66cm}=\sqrt{0^2+5^2}=\sqrt{25}=5.

A(z_A=1-2i) et C(z_C=2+3i) 

Pour calculer la distance AC , on remplace z_A par 1-2i et z_C par 2+3i dans 

AC=|z_C-z_A|.

AC=|(2+3i)-(1-2i)|

\hspace{0.66cm}=|2+3i-1+2i|

\hspace{0.66cm}=|1+5i|

\hspace{0.66cm}=|1+5i|

Pour calculer |1+5i|, on utilise la définition

\hspace{0.66cm}=\sqrt{1^2+5^2}=\sqrt{1+25}=\sqrt{26}.

C(z_C=2+3i) et B(z_B=1+3i) 

Pour calculer la distance CB , on remplace z_C par 2+3i et z_B par 1+3i dans 

CB=|z_B-z_C|.

CB=|(1+3i)-(2+3i)|

\hspace{0.66cm}=|1+3i-2-3i|

\hspace{0.66cm}=|-1|

\hspace{0.66cm}=1.

O(z_O=0) et A(z_A=1-2i) 

Pour calculer la distance OA , on remplace z_O par 0 et z_A par 1-2i dans 

OA=|z_A-z_O|.

OA=|(1-2i)-0|

\hspace{0.66cm}=|1-2i|

On utilise la définition du module.

\hspace{0.66cm}=\sqrt{1^2+(-2)^2}

\hspace{0.66cm}=\sqrt{1+4}

\hspace{0.66cm}=\sqrt{5}

z_A=1+i , z_B=1-i , z_J=i\sqrt{2} et z_K=-\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}

On veut déterminer z_L l’affixe du point L.

L le symétrique du point J par rapport au point K donc K est le milieu du segment [LJ].

Donc z_K=\frac{z_L+z_J}{2}

On remplace z_K par -\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i et z_J par \sqrt{2}i dans

z_K=\frac{z_L+z_J}{2}.

-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i=\frac{z_L+\sqrt{2}i}{2}

On écrit l’égalité dans l’autre sens pour plus de facilité.

\frac{z_L+\sqrt{2}i}{2}=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i

On multiplie par 2 de chaque côté.

z_L+\sqrt{2}i=2\times(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)

z_L+\sqrt{2}i=-\sqrt{2}+\sqrt{2}i

\sqrt{2}i n’est pas à sa place dans le membre de gauche, on l’enlève de chaque côté.

z_L=-\sqrt{2}

On vérifie avec Géogébra.

Pour montrer que les points A,B,J et L appartiennent au cercle de O er de rayon \sqrt{2}, on va montrer que les distances OA , OB , OJ et OL sont égales au rayon \sqrt{2}.

Pour calculer la distance OA , on remplace z_A par 1+i 

OA=|z_A|

\hspace{0.66cm}=|1+i|

\hspace{0.66cm}=\sqrt{1^2+1^2}

\hspace{0.66cm}=\sqrt{1+1}

\hspace{0.66cm}=\sqrt{2}

Pour calculer la distance OB , on remplace z_B par 1-i qui est égal à \overline{z_A}

OB=|z_B|\\\hspace{0.66cm}=|\overline{z_A}|.

\hspace{0.66cm}=|z_A|.

\hspace{0.66cm}=\sqrt{2}

Pour calculer la distance OJ , on remplace z_J par \sqrt{2}i 

OJ=|z_J|\\\hspace{0.66cm}=|\sqrt{2}i|

\hspace{0.66cm}=\sqrt{0^2+\sqrt{2}^2}

\hspace{0.66cm}=\sqrt{0+2}

\hspace{0.66cm}=\sqrt{2}

Pour calculer la distance OL , on remplace z_L par -\sqrt{2} 

OL=|z_L|\\\hspace{0.66cm}=|-\sqrt{2}|

\hspace{0.66cm}=\sqrt{(-\sqrt{2})^2+0^2}

\hspace{0.66cm}=\sqrt{2+0}

\hspace{0.66cm}=\sqrt{2}

On a  montré que les distances OA , OB , OJ et OL sont égales au rayon \sqrt{2} donc  les points A,B,J et L appartiennent au cercle de O er de rayon \sqrt{2}.

On vérifie avec Géogébra.

z_A=5+i et z_B=6+5i.

On veut déterminer l’ensemble des points M d’affixe z qui vérifient |z-5-i|=2.

Il n’y a z que d’un côté, on modifie l’égalité |z-5-i|=2 sous la forme |z–z_I|=R\\|z–(5+i)|=2\\|z–z_A|=2 

On traduit dans le langage des points. 

AM=2 

L’ensemble cherché est donc le cercle de centre A et de rayon 2.

z_A=5+i et z_B=6+5i.

On veut déterminer l’ensemble des points M d’affixe z qui vérifient |z-5-i|=|z-6-5i|

Il y a z des deux côtés, on modifie l’égalité |z-5-i|=|z-6-5i| sous la forme |z–z_A|=|z–z_B|. 

|z–(5+i)|=|z–(6+5i)|\\|z–z_A|=|z–z_B|

On traduit dans le langage des points. 

AM=BM

L’ensemble cherché est donc la médiatrice de  [AB].

z_C=6-i et z_D=-5+2i.

On veut déterminer l’ensemble des points M d’affixe z qui vérifient |z+5-2i|=|z-6+i|

Il y a z des deux côtés, on modifie l’égalité |z+5-2i=|z-6+i| sous la forme |z–z_A|=|z–z_B|. 

|z–(-5+2i)|=|z–(6-i)|\\|z–z_D|=|z–z_C|

On traduit dans le langage des points. 

DM=CM

L’ensemble cherché est donc la médiatrice du segment [DC].

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.