logo

TE. Complexes et géométrie : argument et forme trigonométrique.

Sommaire

Définition : Argument d’un complexe.

Soit z un nombre complexe et M le point d’affixe z.

Un argument de z est une mesure en radian de l’angle orienté (\overrightarrow{u},\overrightarrow{OM}), on le note arg(z)

Déterminer un argument d’un complexe à l’aide de Géogébra : exemple n°1

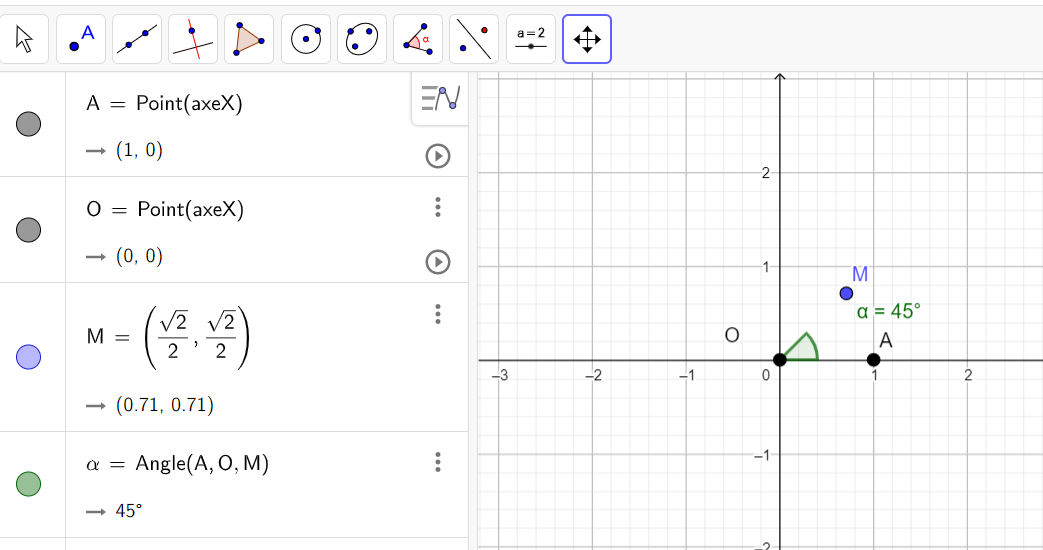
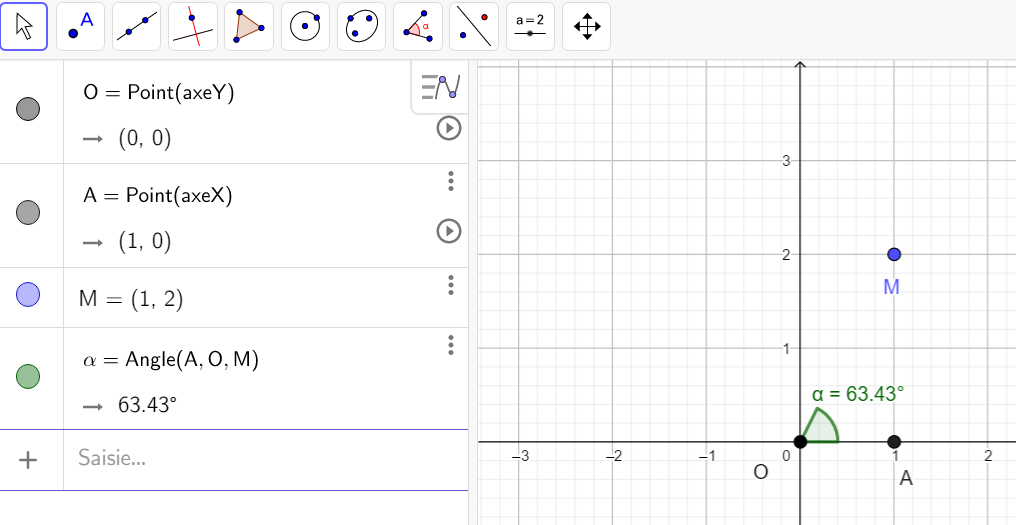
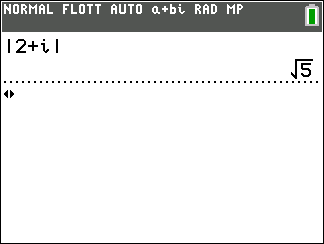
Soit le complexe suivant 2+2i.

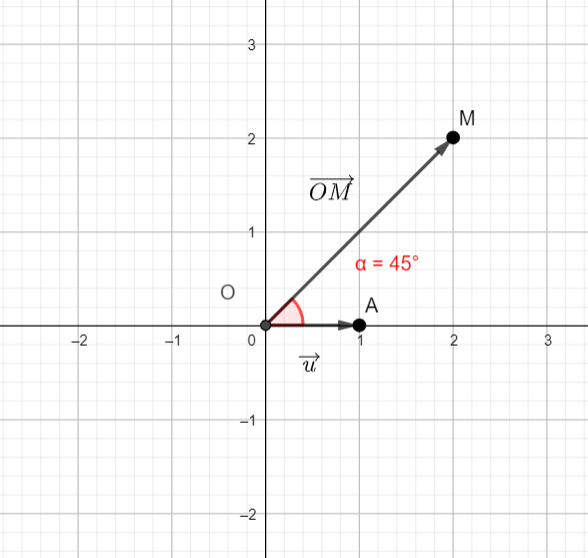
  1. Placer les points O(0,0) , A(1,0) et M(2,2). Pour cela on peut, par exemple,  taper  O=(0,0) dans la colonne Algèbre ( celle de gauche).
  2. Mesurer l’angle orienté (\overrightarrow{u},\overrightarrow{OM}). Pour cela cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Angle dans le menu déroulant. Dans le repère cliquer sur les points A , O et M dans cet ordre, s’affiche alors \alpha=45°.
  3. Pour conclure, comme il s’agit d’un angle orienté, on regarde si on va de \overrightarrow{u} vers \overrightarrow{OM} dans le sens trigonométrique (sens inverse des aiguilles d’une montre ) ou pas; ici on va dans le sens trigonométrique donc la mesure est positive. Pour obtenir la mesure en radians on utilise la proportionnalité :

\pi

?

180°

45°

Donc (\overrightarrow{u},\overrightarrow{OM})=\frac{45\pi}{180}=\frac{\pi}{4}.

Déterminer un argument d’un complexe à l’aide de Géogébra : exemple n°2

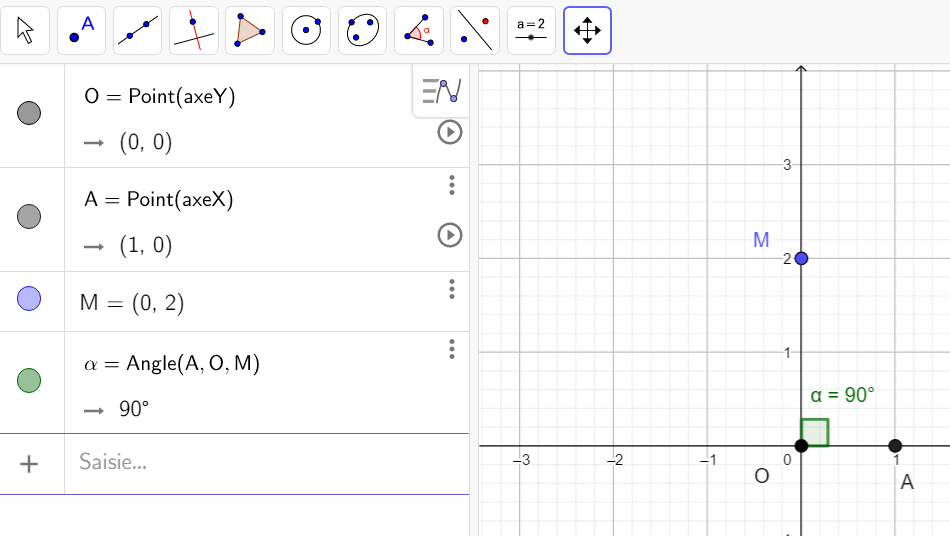
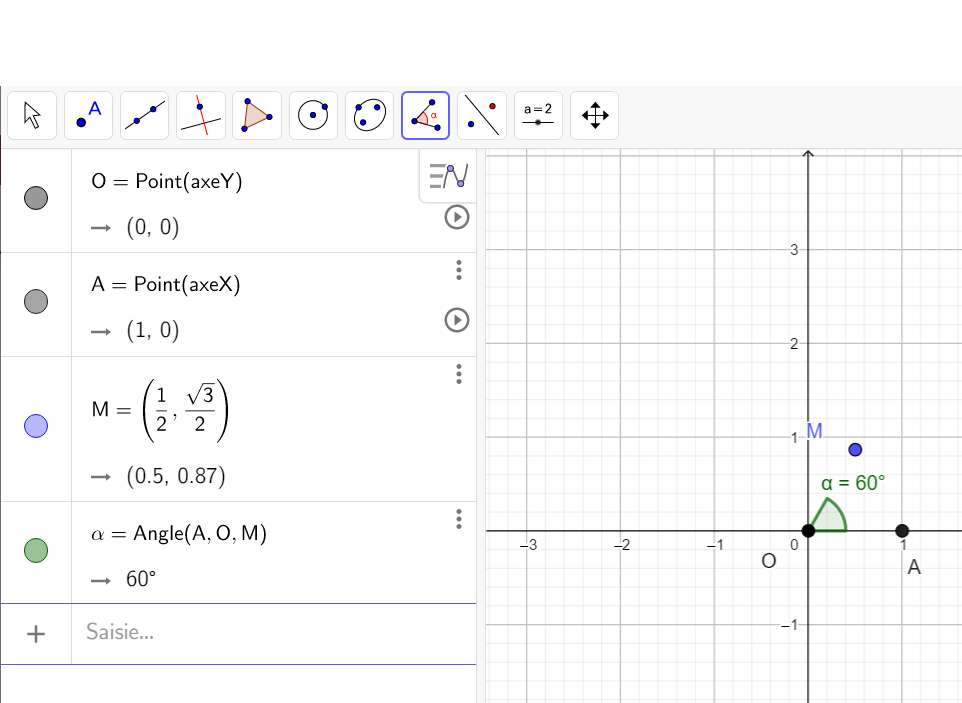
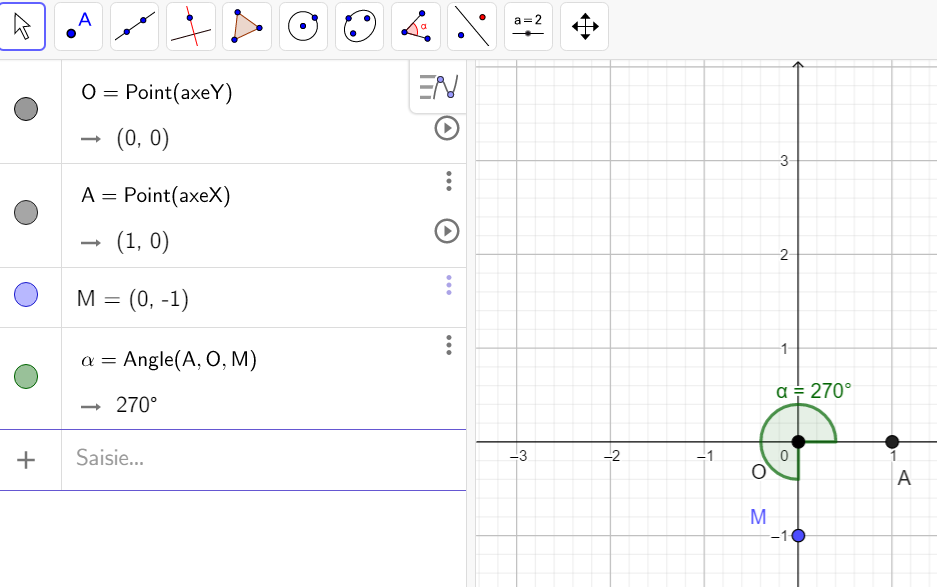
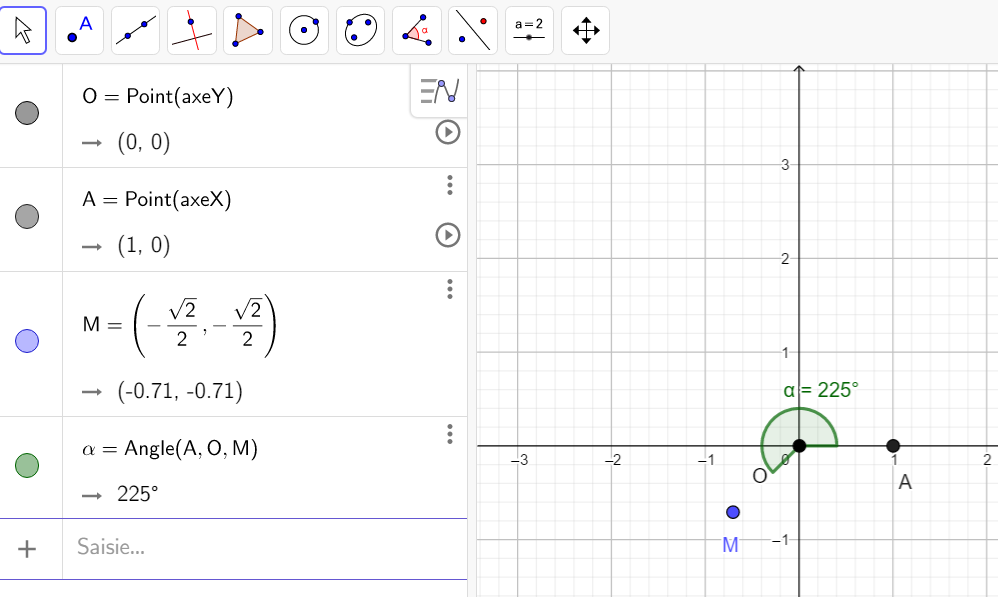
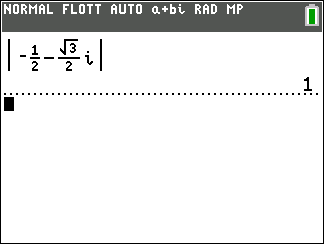
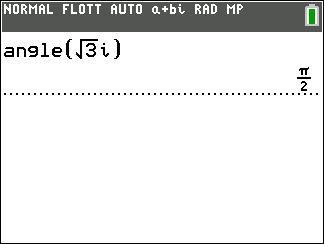
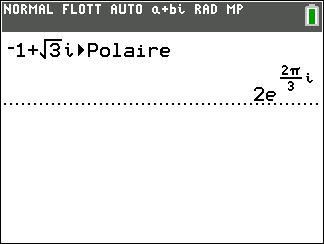
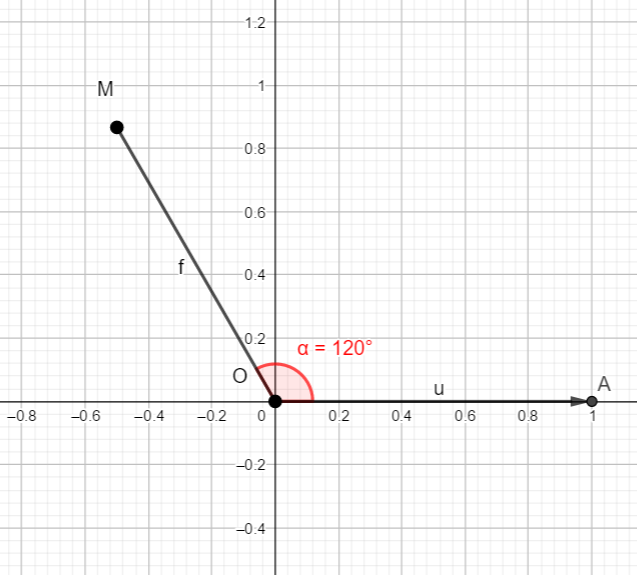
Soit le complexe -\frac{1}{2}+i\frac{\sqrt{3}}{2}.

  1. Placer les points O(0,0) , A(1,0) et M(-\frac{1}{2},\frac{\sqrt{3}}{2}). Pour cela on peut, par exemple,  taper  O=(0,0) dans la colonne Algèbre ( celle de gauche).
  2. Mesurer l’angle orienté (\overrightarrow{u},\overrightarrow{OM}). Pour cela cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Angle dans le menu déroulant. Dans le repère cliquer sur les points A , O et M dans cet ordre, s’affiche alors \alpha=120°.
  3. Pour conclure, comme il s’agit d’un angle orienté, on regarde si on va de \overrightarrow{u} vers \overrightarrow{OM} dans le sens trigonométrique (sens inverse des aiguilles d’une montre ) ou pas; ici on va dans le sens trigonométrique donc la mesure est positive. Pour obtenir la mesure en radians on utilise la proportionnalité :

\pi

?

180°

120°

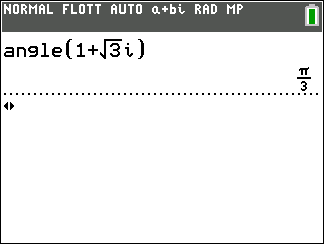
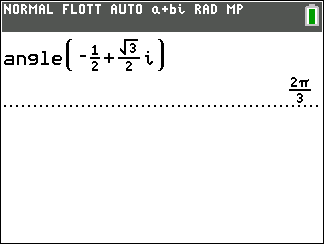
Donc (\overrightarrow{u},\overrightarrow{OM})=\frac{120\pi}{180}=\frac{2\pi}{3}.

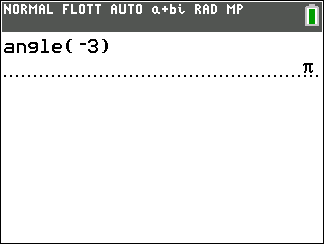
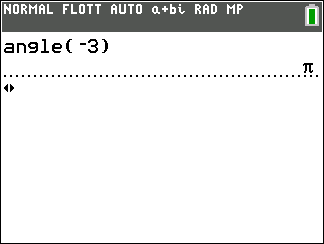
Méthode pour calculer un argument d’un complexe avec la TI 83 premium CE.

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

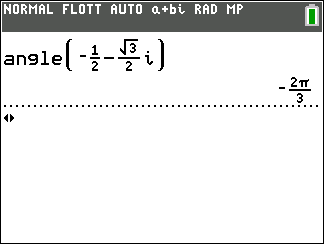
Sur la 4ème ligne sélectionner angle( , puis saisir à la suite le nombre complexe.

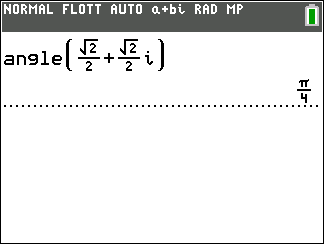
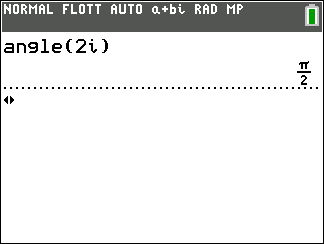
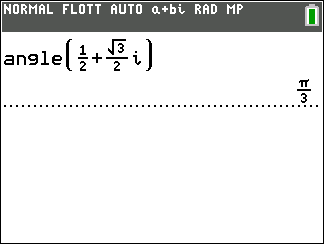
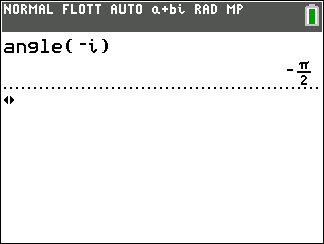
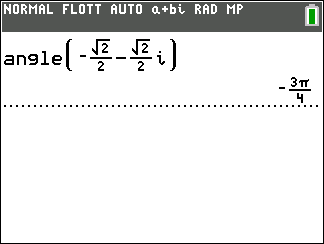
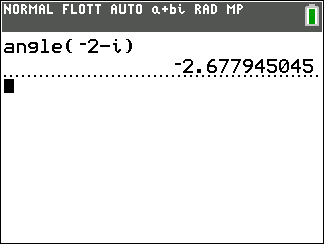
Exemple : vérifions le résultat obtenu à l’exemple n°2 

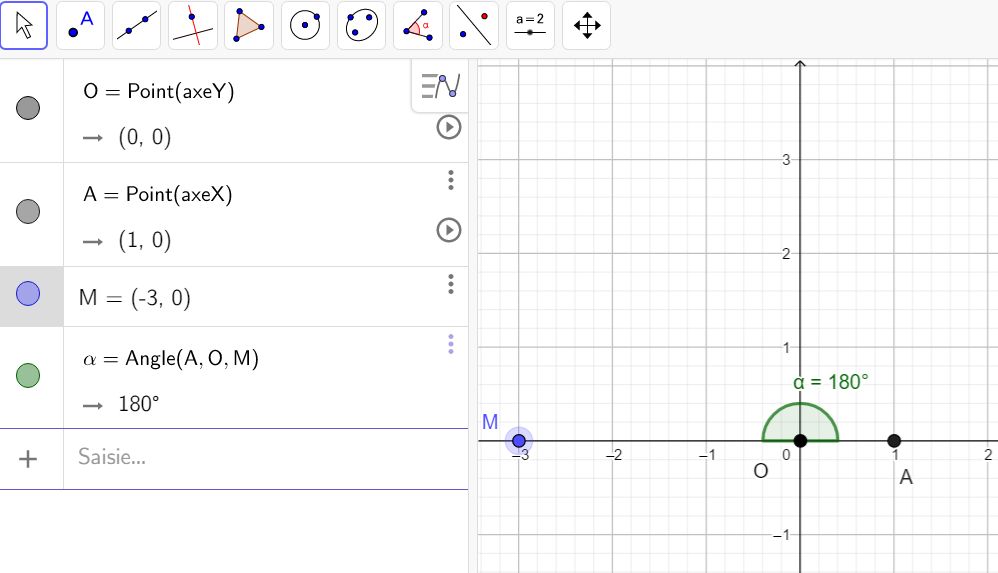
Exercice n°1

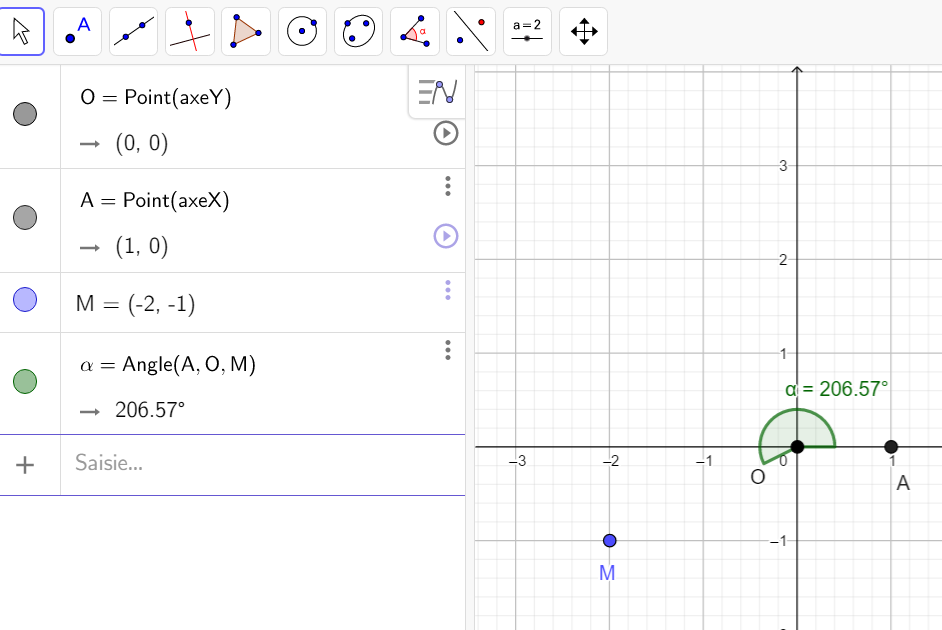
A l’aide de la fenêtre Géogébra ci-dessous, déterminer arg(z) dans chaque cas. Pour cela 

  1. Placer le point M d’affixe z
  2. Mesurer l’angle orienté (\overrightarrow{OA},\overrightarrow{OM}).
  3. En déduire les mesures de arg(z).

On peut ensuite vérifier le résultat à l’aide de la TI 83 Premium CE.

z_1=\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}
correction
je vérifie avec ma TI 83
z_2=2i
correction
je vérifie avec ma TI 83
z_3=-3
correction
je vérifie avec ma TI 83
z_4=\frac{1}{2}+i\frac{\sqrt{3}}{2}
correction
je vérifie avec ma TI 83
z_5=-i
correction
je vérifie avec ma TI 83
z_6=2
correction
je vérifie avec ma TI 83
z_7=-\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}
correction
je vérifie avec ma TI 83
z_8=1+2i
correction
je vérifie avec ma TI 83
z_9=-2-i
correction
je vérifie avec ma TI 83

Propriétés des argument d’un complexe.

Soit z un nombre complexe non nul.

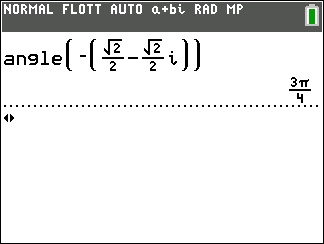
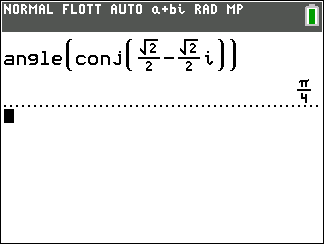
z \in \mathbf{R}^{+}\iff arg(z)=0[2\pi]\\z est un imaginaire pur avec une partie imaginaire positive \iff arg(z)=\frac{\pi}{2}[2\pi]\\z \in \mathbf{R}^{-}\iff arg(z)=\pi [2\pi]\\z est un imaginaire pur avec une partie imaginaire négative \iff arg(z)=-\frac{\pi}{2}[2\pi]\\arg(-z)=arg(z)+\pi[2\pi]\\arg(\overline{z})=-arg(z)[2\pi]

Exercice n°2

A l’aide des propriétés précédentes, déterminer arg(z) dans chaque cas.

z_1=-6i
correction
je vérifie avec ma TI 83
z_2=2i
correction
je vérifie avec ma TI 83
z_3=-3
correction
je vérifie avec ma TI 83

Exercice n°3

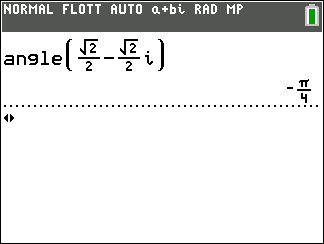
Soit z=\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}

  1. Déterminer arg(z) à l’aide de la calculatrice.
correction

2. A l’aide des propriétés précédentes, déterminer :

arg(-z)
correction
je vérifie avec ma TI 83
arg(\overline{z})
correction
je vérifie avec ma TI 83

Théorème : déterminer un argument par le calcul

Soit z un nombre complexe non nul tel que z=a+ib.

Alors un argument de z est un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

Exemple n°1

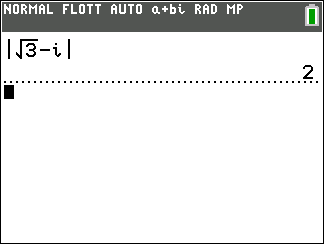
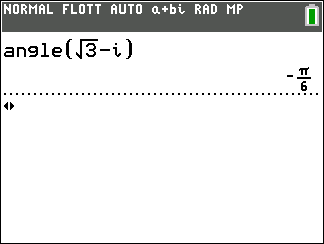
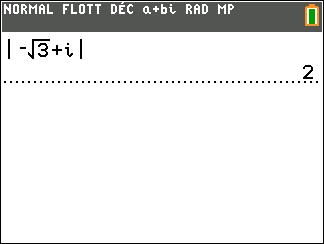
On veut déterminer un argument de z=-\sqrt{3}+i

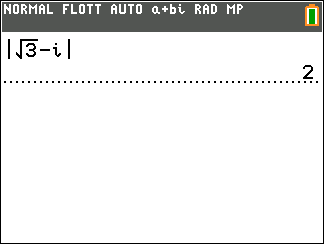
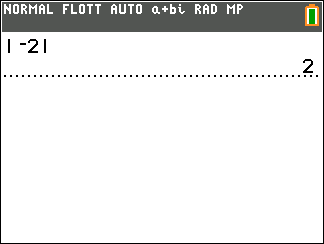
  1. On calcule le module de z

On remplace a par la partie rélle de z qui vaut -\sqrt{3} et b par la partie imaginaire de z qui vaut 1 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-\sqrt{3})^2+1^2}

\hspace{0.5cm}=\sqrt{3+1}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

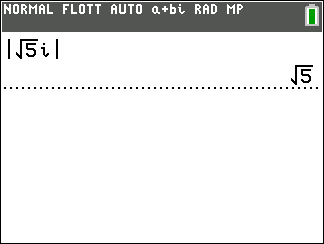
On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut -\sqrt{3} et b par la partie imaginaire de z qui vaut 1 et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{-\sqrt{3}}{2} et sin(\Theta)=\frac{1}{2}

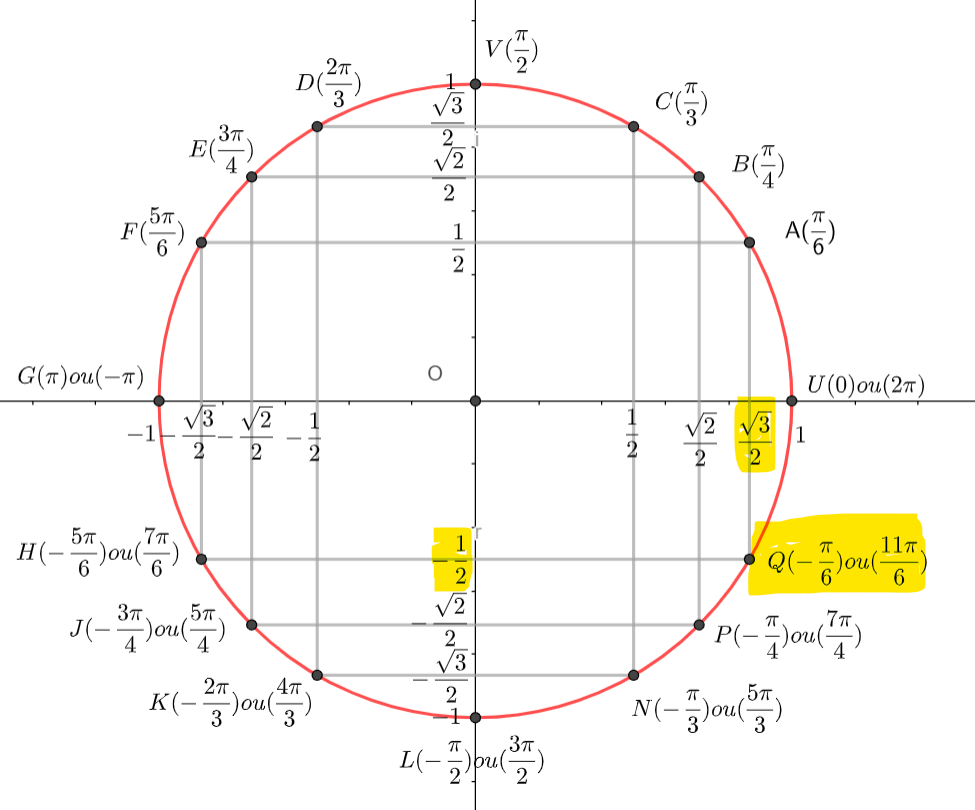
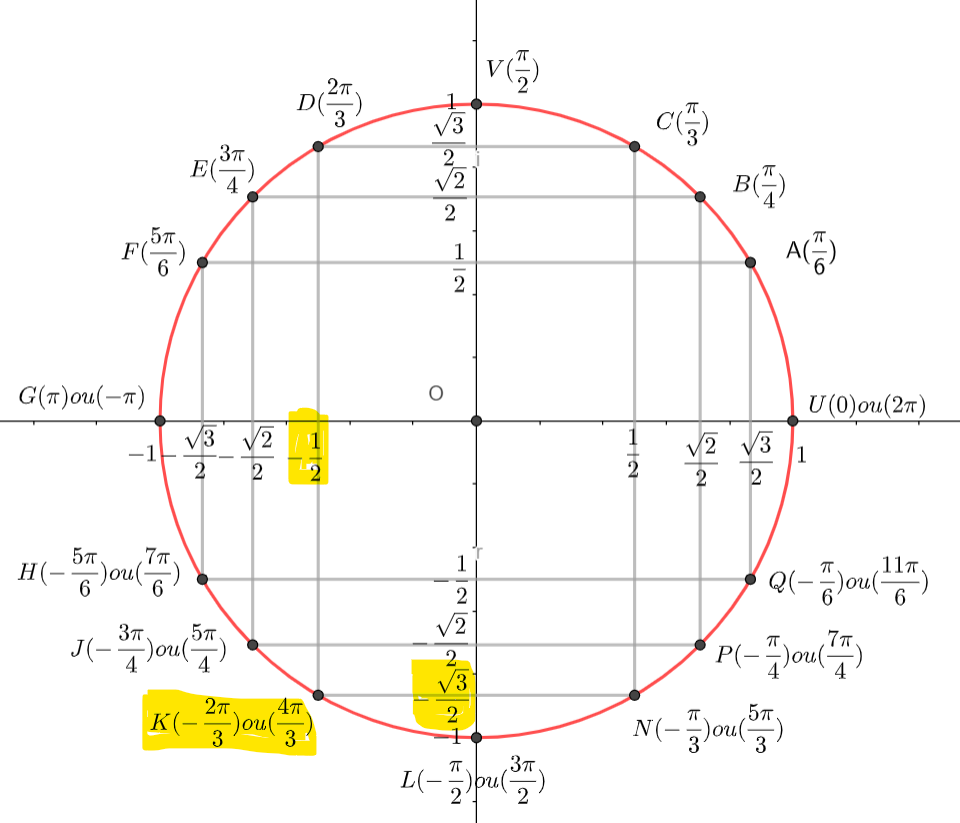
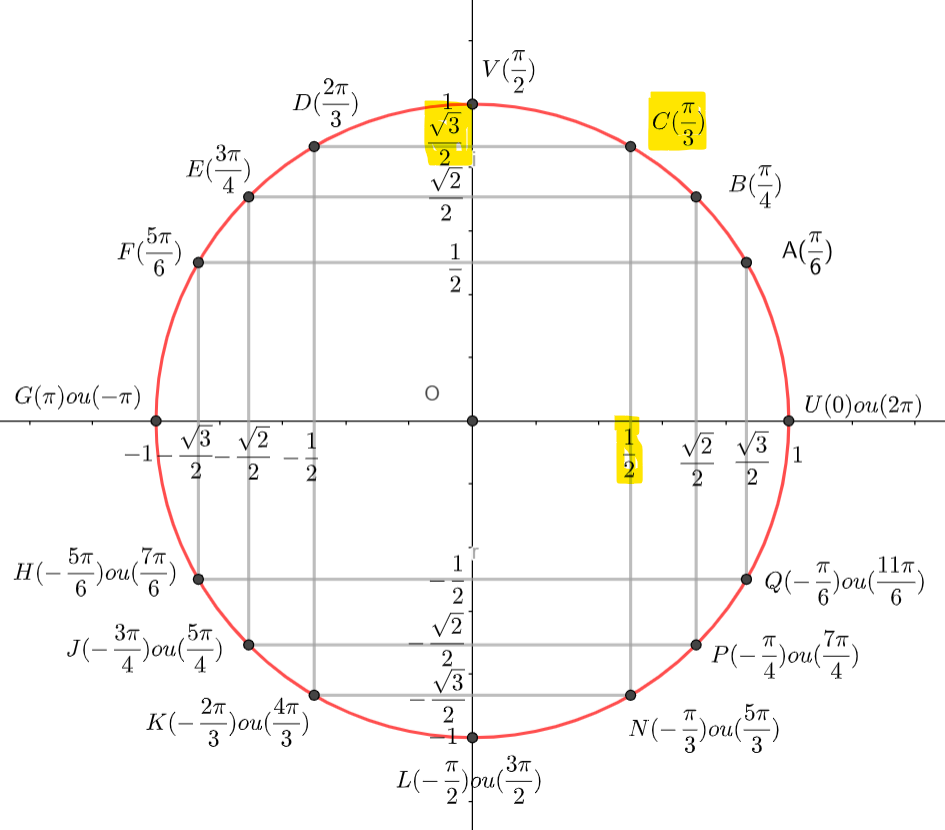
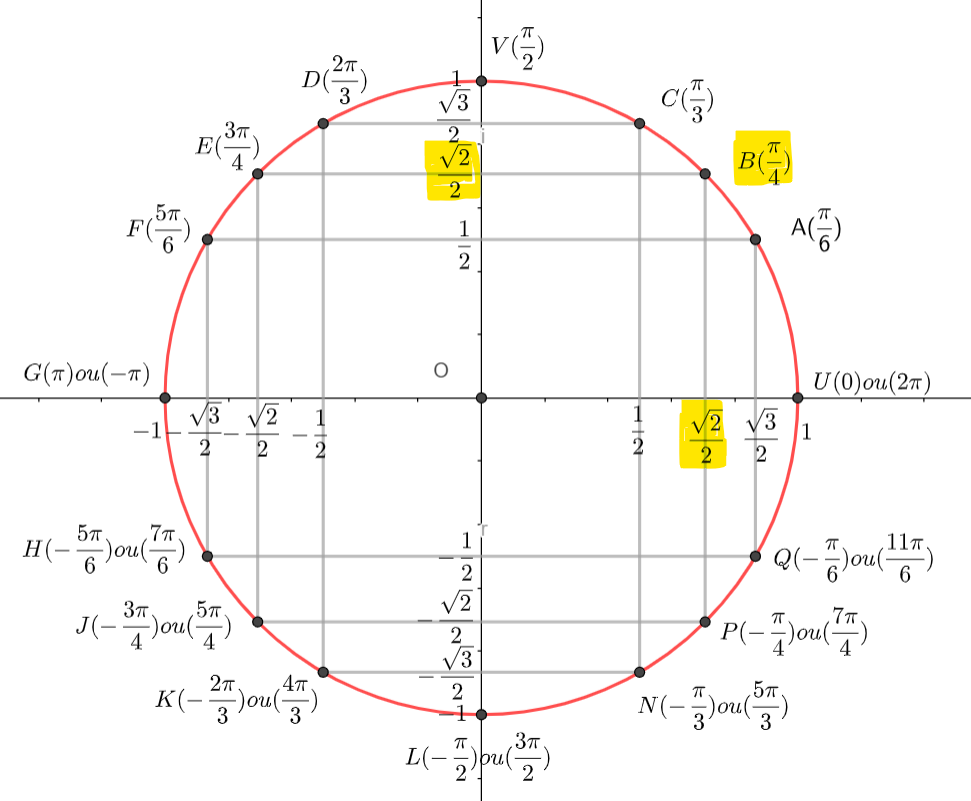
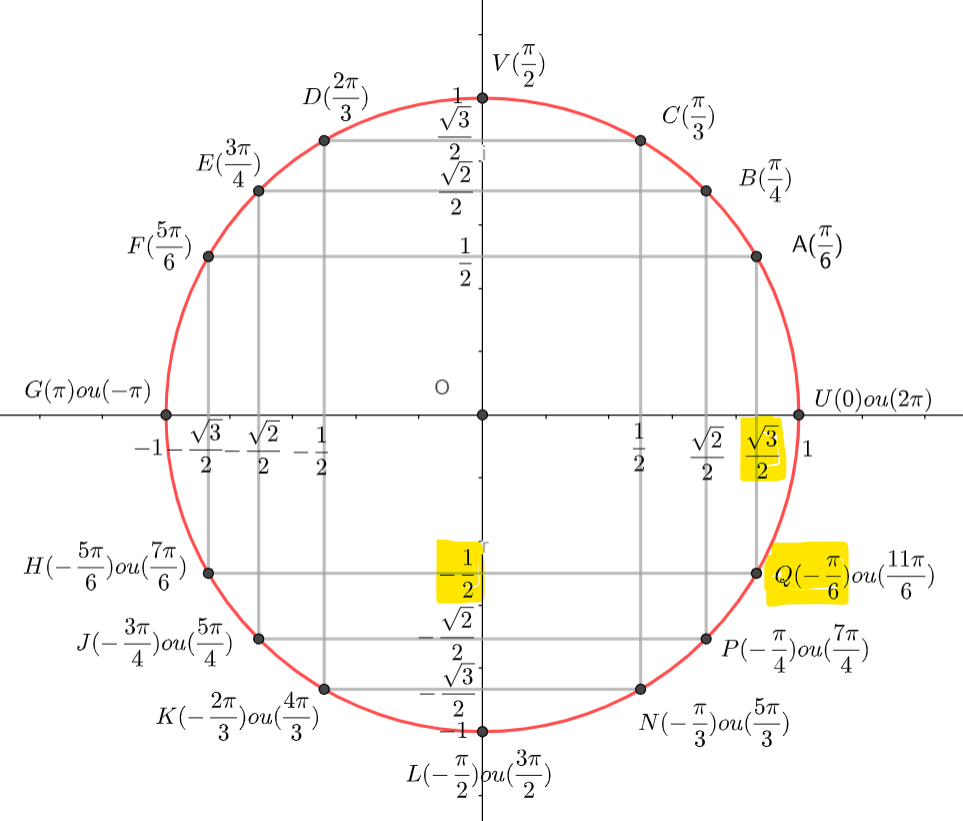
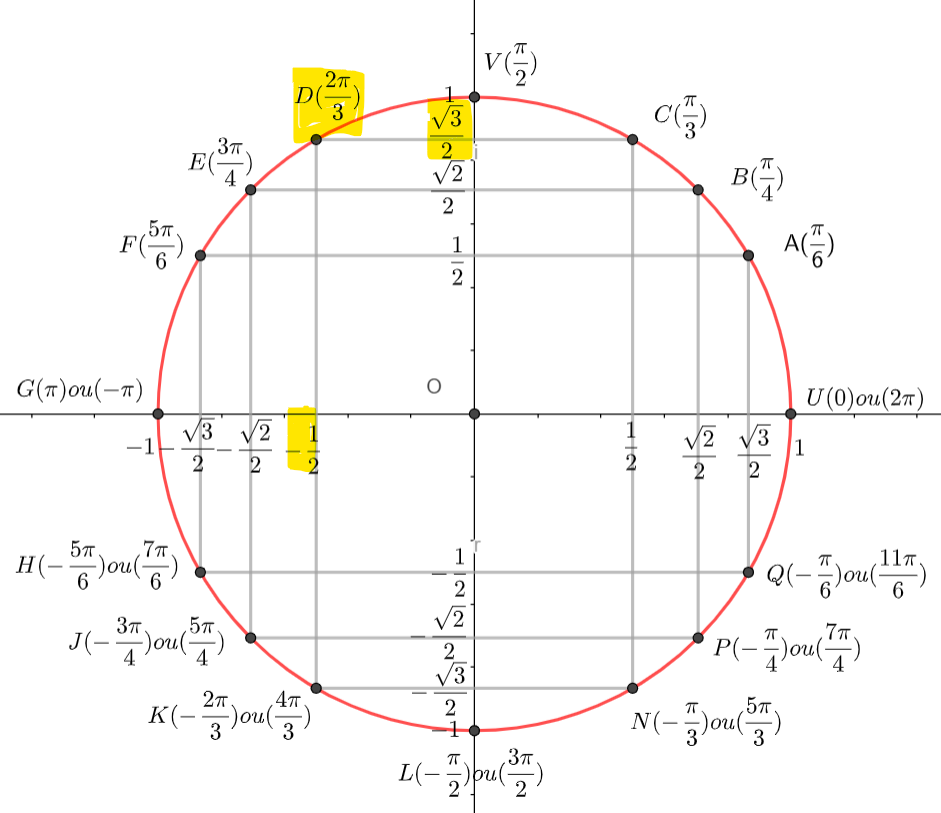
Pour déterminer une valeur de \Theta, on peut utiliser le cercle suivant :

On place \frac{-\sqrt{3}}{2} sur l’axe des abscisses, \frac{1}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{5\pi}{6}. attention il y a une infinité de mesures : \frac{5\pi}{6}+2k\pi.

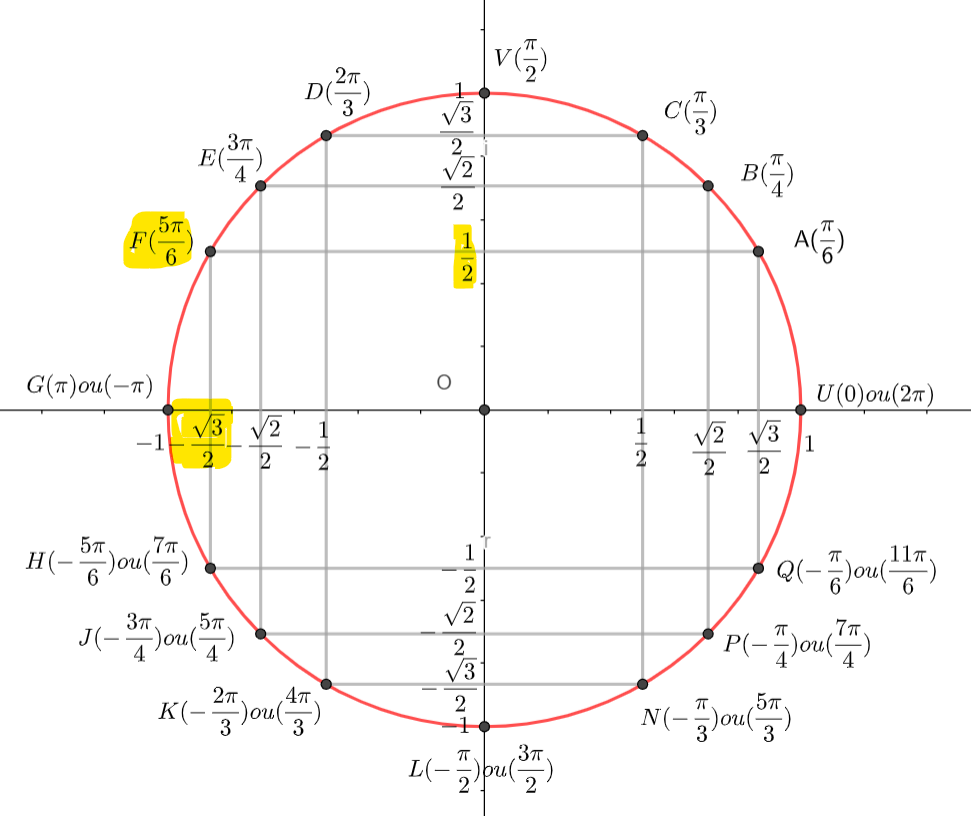
Donc arg(z)=\frac{5\pi}{6}[2\pi].

Exemple n°2

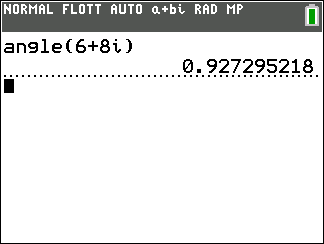
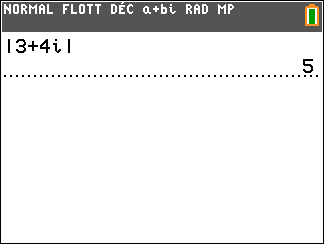
On veut déterminer un argument de z=3+4i

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut 4 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{3^2+4^2}

\hspace{0.5cm}=\sqrt{9+16}

\hspace{0.5cm}=\sqrt{25}

\hspace{0.5cm}=5

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut 4 et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{3}{5} et sin(\Theta)=\frac{4}{5}

Pour déterminer une valeur de \Theta, on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{3}{5}

\Theta=cos^{-1}(\frac{3}{5})

La  calculatrice donne \Theta=0.93

En réalité on obtient :

\Theta=0.93 ou \Theta=-0.93

sin(\Theta)=\frac{4}{5}

\Theta=sin^{-1}(\frac{4}{5})

La  calculatrice donne \Theta=0.93

En réalité on obtient :

\Theta=0.93 ou \Theta=\pi-0.93

La solution commune aux deux équations est : \Theta=0.93.

Donc arg(z)=0.93[2\pi].

Exercice n°4

Déterminer arg(z) dans chaque cas par le calcul.

z=\sqrt{3}-i
correction
je vérifie avec ma TI 83
z=-\frac{1}{2}-i\frac{\sqrt{3}}{2}
correction
je vérifie avec ma TI 83
z=2
correction
je vérifie avec ma TI 83
z=6+8i
correction
je vérifie avec ma TI 83
z=\sqrt{3}i
correction
je vérifie avec ma TI 83
z=1+i\sqrt{3}
correction
je vérifie avec ma TI 83

Théorème : égalité de deux complexes

Deux nombres complexes non nuls sont égaux si et seulement si ils ont même module et même argument ( modulo 2\pi).

Définition : forme trigonométrique

Tout nombre complexe z peut s’écrire sous la forme z=r(cos(\Theta)+isin(\Theta))

avec r=|z| et \Theta=arg(z)[2\pi].

Cette écriture est appelée forme trigonométrique de z.

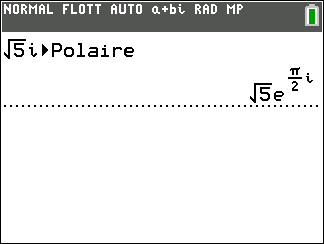
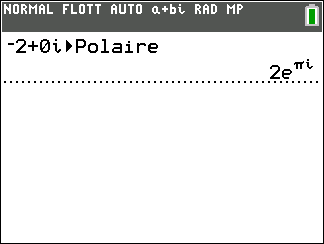
Méthode pour déterminer le module et un argument d’un complexe avec la TI 83 premium CE dans le but de le mettre sous forme trigonométrique.

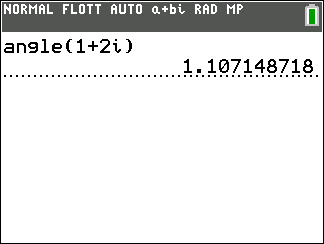
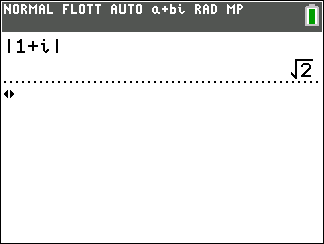
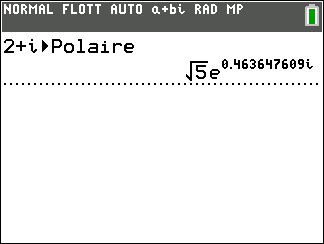
Saisir le nombre complexe, par exemple  1+i

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

Sur la 7ème ligne sélectionner Polaire.

Puis faire entrer

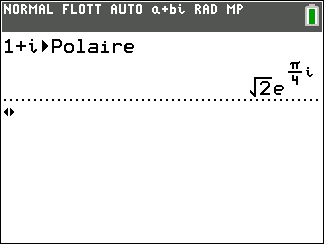
En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de 1+i est \sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4})

Exemple n°3

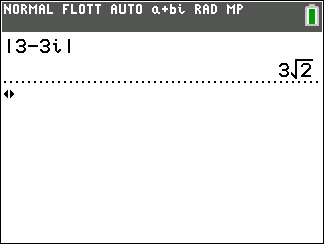
On veut déterminer la forme trigonométrique de z=3-3i

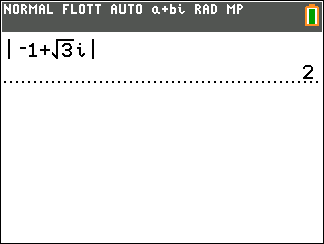
  1. On calcule le module de z

On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut -3 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{3^2+(-3)^2}

\hspace{0.5cm}=\sqrt{9+9}

\hspace{0.5cm}=\sqrt{18}

\hspace{0.5cm}=\sqrt{9\times 2}

\hspace{0.5cm}=\sqrt{9}\times \sqrt{2}

\hspace{0.5cm}=3\sqrt{2}

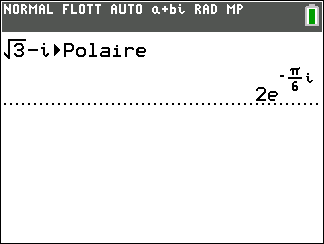
On peut vérifier avec la TI 83 Premium CE

2. On cherche un argument de z noté \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut -3 et |z| par 3\sqrt{2} dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{3}{3\sqrt{2}} et sin(\Theta)=\frac{-3}{3\sqrt{2}}\\cos(\Theta)=\frac{1}{\sqrt{2}} et sin(\Theta)=\frac{-1}{\sqrt{2}}\\cos(\Theta)=\frac{\sqrt{2}}{2} et sin(\Theta)=\frac{-\sqrt{2}}{2}

Pour déterminer une valeur de \Theta, on peut utiliser le cercle suivant :

On place \frac{\sqrt{2}}{2} sur l’axe des abscisses, -\frac{\sqrt{2}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici -\frac{\pi}{4}. attention il y a une infinité de mesures : -\frac{\pi}{4}+2k\pi.

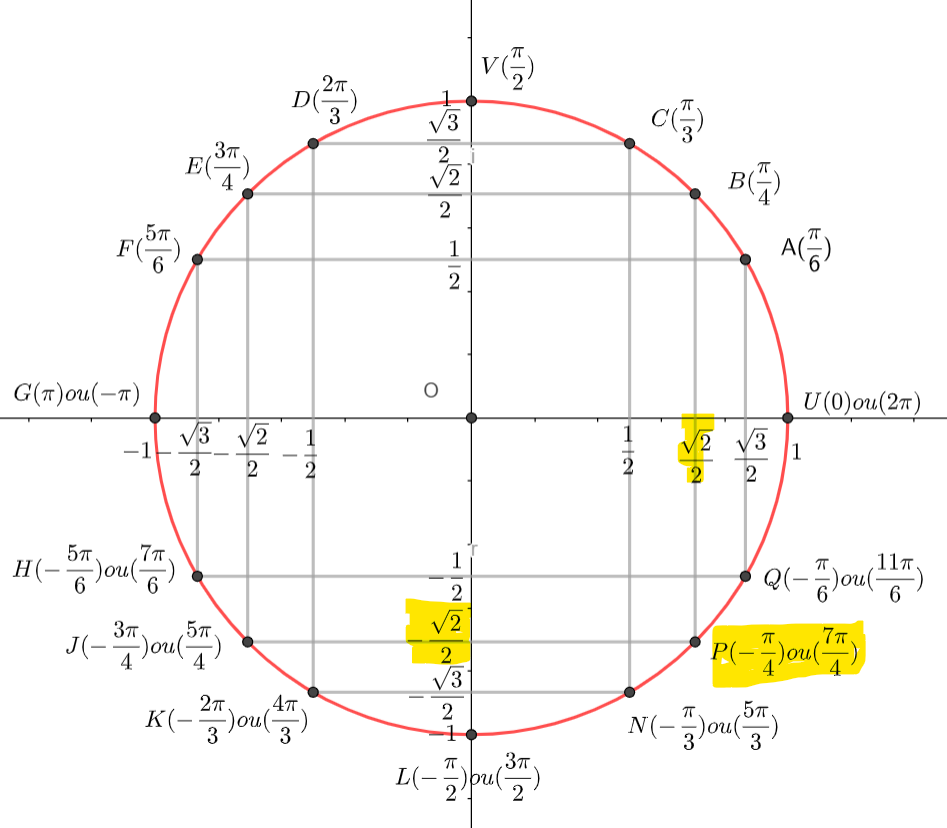
Donc arg(z)=-\frac{\pi}{4}[2\pi].

3. On en déduit la forme trigonométrique de z.

z=3\sqrt{2}(cos(-\frac{\pi}{4})+isin(-\frac{\pi}{4}).

Exercice n°5

Ecrire z sous forme trigonométrique dans chaque cas.

z=1+i
correction
je vérifie avec ma TI 83
z=\sqrt{5}i
correction
je vérifie avec ma TI 83
z=\sqrt{3}-i
correction
je vérifie avec ma TI 83
z=-2
correction
je vérifie avec ma TI 83
z=-1+\sqrt{3}i
correction
je vérifie avec ma TI 83
z=2+i
correction
je vérifie avec ma TI 83

©2020 – Math’O karé SAS

Pour placer M, mieux vaut saisir M=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive).

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{45\times\pi}{180}=\frac{\pi}{4}.

Pour obtenir tous les arguments, on écrit :

arg(z_1)=\frac{\pi}{4}+2k\pi
\pi?
180°45°

Pour placer M, mieux vaut saisir M=(0,2) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive).

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{90\times\pi}{180}=\frac{\pi}{2}.

Pour obtenir tous les arguments, on écrit :

arg(z_2)=\frac{\pi}{2}+2k\pi
\pi?
180°90°

Pour placer M, mieux vaut saisir M=(-3,0) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive).

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\pi.

Pour obtenir tous les arguments, on écrit :

arg(z_3)=\pi+2k\pi

 

Pour placer M, mieux vaut saisir M=(\frac{1}{2},\frac{\sqrt{3}}{2}) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive). 

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{60\times\pi}{180}=\frac{\pi}{3}.

Pour obtenir tous les arguments, on écrit :

arg(z_4)=\frac{\pi}{3}+2k\pi
\pi?
180°60°

Pour placer M, mieux vaut saisir M=(0,-1) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive).

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{270\times\pi}{180}=\frac{3\pi}{2}.

Pour obtenir tous les arguments, on écrit :

arg(z_5)=\frac{3\pi}{2}+2k\pi

Remarque pour k=-1 ,

arg(z_5)=\frac{3\pi}{2}-2\pi

arg(z_5)=\frac{3\pi}{2}-\frac{4\pi}{2}

arg(z_5)=-\frac{\pi}{2} , c’est la mesure qu’on obtient en tournant dans le sens des aiguilles d’une montre ( le sens inverse du sens trigonométrique).

\pi?
180°270°

Pour placer M, mieux vaut saisir M=(2,0) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive).

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=0.

Pour obtenir tous les arguments, on écrit :

arg(z_6)=2k\pi

 

Pour placer M, mieux vaut saisir M=(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive). 

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{225\times\pi}{180}=\frac{5\pi}{4}.

Pour obtenir tous les arguments, on écrit :

arg(z_7)=\frac{5\pi}{4}+2k\pi

Remarque pour k=-1 ,

arg(z_7)=\frac{5\pi}{4}-2\pi

arg(z_7)=\frac{5\pi}{4}-\frac{8\pi}{4}

arg(z_7)=-\frac{3\pi}{4} , c’est la mesure qu’on obtient en tournant dans le sens des aiguilles d’une montre ( le sens inverse du sens trigonométrique).

\pi?
180°225°

Pour placer M, mieux vaut saisir M=(1,2) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive). 

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{63.43\times\pi}{180}=1.11.

Pour obtenir tous les arguments, on écrit :

arg(z_8)=1.11+2k\pi

 

 

\pi?
180°63.43°

Pour placer M, mieux vaut saisir M=(-2,-1) dans la colonne Algèbre située à gauche de la fenêtre Géogébra en utilisant le clavier Géogébra accessible en cliquant sur le petit clavier situé en bas de l’écran à gauche.

Ensuite on clique sur le 8ème onglet en haut à partir de la gauche et on sélectionne Angle dans le menu déroulant. Il ne reste plus qu’à cliquer dans l’ordre sur les points A , O et M.

On utilise la proportionnalité pour déterminer en radian une mesure de l’angle suivant (Géogébra donne toujours la mesure positive). 

\widehat{\overrightarrow{OA},\overrightarrow{OM}}=\frac{206.57\times\pi}{180}=3.61.

Pour obtenir tous les arguments, on écrit :

arg(z_9)=3.61+2k\pi

 

\pi?
180°206.57°

z_1=-6i est un imaginaire pur avec une partie imaginaire négative donc arg(z_1)=-\frac{\pi}{2}[2\pi]

z_2=2i est un imaginaire pur avec une partie imaginaire positive donc arg(z_2)=\frac{\pi}{2}[2\pi]

z_3=-3 est un réel négatif donc arg(z_3)=\pi[2\pi].

 Pour déterminer arg(-z), on va utiliser arg(-z)=arg(z)+\pi[2\pi] en remplaçant arg(z) par -\frac{\pi}{4}.

arg(-z)=-\frac{\pi}{4}+\pi[2\pi]

arg(-z)=-\frac{\pi}{4}+\frac{4\pi}{4}[2\pi]

arg(-z)=\frac{3\pi}{4}[2\pi]

 Pour déterminer arg(\overline{z}), on va utiliser arg(\overline{z})=-arg(z)[2\pi] en remplaçant arg(z) par -\frac{\pi}{4}.

arg(\overline{z})=-(-\frac{\pi}{4})[2\pi]\\arg(\overline{z})=\frac{\pi}{4}[2\pi]

 

On veut déterminer un argument de z=\sqrt{3}-i

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut \sqrt{3} et b par la partie imaginaire de z qui vaut -1 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(\sqrt{3})^2+(-1)^2}

\hspace{0.5cm}=\sqrt{3+1}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut \sqrt{3} et b par la partie imaginaire de z qui vaut -1 et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{\sqrt{3}}{2} et sin(\Theta)=\frac{-1}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{\sqrt{3}}{2}

\Theta=cos^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=\frac{\pi}{6}

En réalité on obtient :

\Theta=\frac{\pi}{6} ou \Theta=-\frac{\pi}{6}

sin(\Theta)=-\frac{1}{2}

\Theta=sin^{-1}(-\frac{1}{2})

La  calculatrice donne \Theta=-\frac{\pi}{6}

En réalité on obtient :

\Theta=-\frac{\pi}{6} ou \Theta=\pi-(-\frac{\pi}{6})

La solution commune aux deux équations est : \Theta=-\frac{\pi}{6}.

Donc arg(z)=-\frac{\pi}{6}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{\sqrt{3}}{2} sur l’axe des abscisses, -\frac{1}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici -\frac{\pi}{6}. attention il y a une infinité de mesures : -\frac{\pi}{6}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=-\frac{\pi}{6}[2\pi].

 

On veut déterminer un argument de z=-\frac{1}{2}-i\frac{\sqrt{3}}{2}

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut -\frac{1}{2} et b par la partie imaginaire de z qui vaut -\frac{\sqrt{3}}{2} dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-\frac{1}{2})^2+(-\frac{\sqrt{3}}{2})^2}

\hspace{0.5cm}=\sqrt{\frac{1}{4}+\frac{3}{4}}

\hspace{0.5cm}=\sqrt{\frac{4}{4}}

\hspace{0.5cm}=\sqrt{1}

\hspace{0.5cm}=1

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut -\frac{1}{2} et b par la partie imaginaire de z qui vaut -\frac{\sqrt{3}}{2} et |z| par 1 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{-\frac{1}{2}}{1} et sin(\Theta)=\frac{-\frac{\sqrt{3}}{2}}{1}\\cos(\Theta)=-\frac{1}{2} et sin(\Theta)=-\frac{\sqrt{3}}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=-\frac{1}{2}

\Theta=cos^{-1}(-\frac{1}{2})

La  calculatrice donne \Theta=\frac{2\pi}{3}

En réalité on obtient :

\Theta=\frac{2\pi}{3} ou \Theta=-\frac{2\pi}{3}

sin(\Theta)=-\frac{\sqrt{3}}{2}

\Theta=sin^{-1}(-\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=-\frac{\pi}{3}

En réalité on obtient :

\Theta=-\frac{\pi}{3} ou \Theta=\pi-(-\frac{\pi}{3})=\frac{4\pi}{3}=-\frac{2\pi}{3}[2\pi]

La solution commune aux deux équations est : \Theta=-\frac{2\pi}{3}.

Donc arg(z)=-\frac{2\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place -\frac{1}{2} sur l’axe des abscisses, -\frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici -\frac{2\pi}{3}. attention il y a une infinité de mesures : -\frac{2\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=-\frac{2\pi}{3}[2\pi].

 

 

On veut déterminer un argument de z=2.

Comme z=2 est un réel positif, d’après les propriétés précédentes,  on a :  arg(z)=0[2\pi].

On veut déterminer un argument de z=6+8i

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 6 et b par la partie imaginaire de z qui vaut 8 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{6^2+8^2}

\hspace{0.5cm}=\sqrt{36+64}

\hspace{0.5cm}=\sqrt{100}

\hspace{0.5cm}=10

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 6 et b par la partie imaginaire de z qui vaut 8 et |z| par 10 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{6}{10} et sin(\Theta)=\frac{8}{10}

Pour déterminer, par le calcul, une valeur de \Theta, on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{6}{10}

\Theta=cos^{-1}(\frac{6}{10})

La  calculatrice donne \Theta=0.93

En réalité on obtient :

\Theta=0.93 ou \Theta=-0.93

sin(\Theta)=\frac{\sqrt{8}}{10}

\Theta=sin^{-1}(\frac{8}{10})

La  calculatrice donne \Theta=0.93

En réalité on obtient :

\Theta=0.93 ou \Theta=\pi-0.93

La solution commune aux deux équations est : \Theta=0.93.

Donc arg(z)=0.93[2\pi].

 

On veut déterminer un argument de z=\sqrt{3}i.

Comme z=\sqrt{3}i est un imaginaire avec une partie imaginaire positive, d’après les propriétés précédentes,  on a :  arg(z)=\frac{\pi}{2}[2\pi].

On veut déterminer un argument de z=1+\sqrt{3}i

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 1 et b par la partie imaginaire de z qui vaut \sqrt{3} dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{1^2+\sqrt{3}^2}

\hspace{0.5cm}=\sqrt{1+3}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 1 et b par la partie imaginaire de z qui vaut \sqrt{3} et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{1}{2} et sin(\Theta)=\frac{\sqrt{3}}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{1}{2}

\Theta=cos^{-1}(\frac{1}{2})

La  calculatrice donne \Theta=\frac{\pi}{3}

En réalité on obtient :

\Theta=\frac{\pi}{3} ou \Theta=-\frac{\pi}{3}

sin(\Theta)=\frac{\sqrt{3}}{2}

\Theta=sin^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=\frac{\pi}{3}

En réalité on obtient :

\Theta=\frac{\pi}{3} ou \Theta=\pi-(\frac{\pi}{3})

La solution commune aux deux équations est : \Theta=\frac{\pi}{3}.

Donc arg(z)=\frac{\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{1}{2} sur l’axe des abscisses, \frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{\pi}{3}. attention il y a une infinité de mesures : \frac{\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=\frac{\pi}{3}[2\pi].

 

On veut écrire z=1+i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 1 et b par la partie imaginaire de z qui vaut 1 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{1^2+1^2}

\hspace{0.5cm}=\sqrt{1+1}

\hspace{0.5cm}=\sqrt{2}

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 1 et b par la partie imaginaire de z qui vaut 1 et |z| par \sqrt{2} dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{1}{\sqrt{2}} et sin(\Theta)=\frac{1}{\sqrt{2}}\\cos(\Theta)=\frac{\sqrt{2}}{2} et sin(\Theta)=\frac{\sqrt{2}}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{\sqrt{2}}{2}

\Theta=cos^{-1}(\frac{\sqrt{2}}{2})

La  calculatrice donne \Theta=\frac{\pi}{4}

En réalité on obtient :

\Theta=\frac{\pi}{4} ou \Theta=-\frac{\pi}{4}

sin(\Theta)=\frac{\sqrt{2}}{2}

\Theta=sin^{-1}(\frac{\sqrt{2}}{2})

La  calculatrice donne \Theta=\frac{\pi}{4}

En réalité on obtient :

\Theta=\frac{\pi}{4} ou \Theta=\pi-(\frac{\pi}{4})

La solution commune aux deux équations est : \Theta=\frac{\pi}{4}.

Donc arg(z)=\frac{\pi}{4}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{\sqrt{2}}{2} sur l’axe des abscisses, \frac{\sqrt{2}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{\pi}{4}. attention il y a une infinité de mesures : \frac{\pi}{4}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=\frac{\pi}{4}[2\pi].

3. On en déduit la forme trigonométrique

z=\sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4}))

 

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de 1+i est \sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4}))

On veut écrire z=\sqrt{5}i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 0 et b par la partie imaginaire de z qui vaut \sqrt{5} dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{0^2+\sqrt{5}^2}

\hspace{0.5cm}=\sqrt{0+5}

\hspace{0.5cm}=\sqrt{5}

On peut vérifier avec la TI 83 Premium CE

2. On détermine l’argument de z=\sqrt{5}i

Comme z=\sqrt{5}i est un imaginaire avec une partie imaginaire positive, d’après les propriétés précédentes,  on a :  arg(z)=\frac{\pi}{2}[2\pi].

3. On en déduit la forme trigonométrique de  z=\sqrt{5}i

z=\sqrt{5}(cos(\frac{\pi}{2})+isin(\frac{\pi}{2}))

 

 

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de \sqrt{5}i est \sqrt{5}(cos(\frac{\pi}{2})+isin(\frac{\pi}{2}))

On veut écrire z=\sqrt{3}-i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut \sqrt{3} et b par la partie imaginaire de z qui vaut -1 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{\sqrt{3}^2+(-1)^2}

\hspace{0.5cm}=\sqrt{3+1}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut \sqrt{3} et b par la partie imaginaire de z qui vaut -1 et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{\sqrt{3}}{2} et sin(\Theta)=-\frac{1}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{\sqrt{3}}{2}

\Theta=cos^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=\frac{\pi}{6}

En réalité on obtient :

\Theta=\frac{\pi}{6} ou \Theta=-\frac{\pi}{6}

sin(\Theta)=-\frac{1}{2}

\Theta=sin^{-1}(-\frac{1}{2})

La  calculatrice donne \Theta=-\frac{\pi}{6}

En réalité on obtient :

\Theta=-\frac{\pi}{6} ou \Theta=\pi-(-\frac{\pi}{6})

La solution commune aux deux équations est : \Theta=-\frac{\pi}{6}.

Donc arg(z)=-\frac{\pi}{6}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{\sqrt{3}}{2} sur l’axe des abscisses, -\frac{1}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{-\pi}{6}. attention il y a une infinité de mesures : -\frac{\pi}{6}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=-\frac{\pi}{6}[2\pi].

3. On en déduit la forme trigonométrique

z=2(cos(-\frac{\pi}{6})+isin(-\frac{\pi}{6}))

 

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de \sqrt{3}-i est 2(cos(-\frac{\pi}{6})+isin(-\frac{\pi}{6}))

On veut écrire z=-2 sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut -2 et b par la partie imaginaire de z qui vaut 0 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-2)^2+0^2}

\hspace{0.5cm}=\sqrt{4+0}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On détermine l’argument de z=-2

Comme z=-2 est un réel négatif, d’après les propriétés précédentes,  on a :  arg(z)=\pi[2\pi].

3. On en déduit la forme trigonométrique de  z=-2

z=2(cos(\pi)+isin(\pi))

 

 

Attention si vous tapez -2 puis Polaire, la machine affiche erreur. Il faut taper -2+0i.

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de -2 est 2(cos(\pi)+isin(\pi))

On veut écrire z=-1+\sqrt{3}i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut -1 et b par la partie imaginaire de z qui vaut \sqrt{3} dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-1)^2+\sqrt{3}^2}

\hspace{0.5cm}=\sqrt{1+3}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut -1 et b par la partie imaginaire de z qui vaut \sqrt{3} et |z| par 2 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=-\frac{1}{2} et sin(\Theta)=\frac{\sqrt{3}}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=-\frac{1}{2}

\Theta=cos^{-1}(-\frac{1}{2})

La  calculatrice donne \Theta=\frac{2\pi}{3}

En réalité on obtient :

\Theta=\frac{2\pi}{3} ou \Theta=-\frac{2\pi}{3}

sin(\Theta)=\frac{\sqrt{3}}{2}

\Theta=sin^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=\frac{\pi}{3}

En réalité on obtient :

\Theta=\frac{\pi}{3} ou \Theta=\pi-(\frac{\pi}{3})=\frac{2\pi}{3}

La solution commune aux deux équations est : \Theta=\frac{2\pi}{3}.

Donc arg(z)=\frac{2\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place -\frac{1}{2} sur l’axe des abscisses, \frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{2\pi}{3}. attention il y a une infinité de mesures : \frac{2\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=\frac{2\pi}{3}[2\pi].

3. On en déduit la forme trigonométrique

z=2(cos(\frac{2\pi}{3})+isin(\frac{2\pi}{3}))

 

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de -1+\sqrt{3}i est 2(cos(\frac{2\pi}{3})+isin(\frac{2\pi}{3}))

On veut écrire z=2+i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 2 et b par la partie imaginaire de z qui vaut 1 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{2^2+1^2}

\hspace{0.5cm}=\sqrt{4+1}

\hspace{0.5cm}=\sqrt{5}

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut 2 et b par la partie imaginaire de z qui vaut 1 et |z| par \sqrt{5} dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{2}{\sqrt{5}} et sin(\Theta)=\frac{1}{\sqrt{5}}

Pour déterminer, par le calcul, une valeur de \Theta, on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=\frac{2}{\sqrt{5}}

\Theta=cos^{-1}(\frac{2}{\sqrt{5}})

La  calculatrice donne \Theta=0.46

En réalité on obtient :

\Theta=0.46 ou \Theta=-0.46

sin(\Theta)=\frac{1}{\sqrt{5}}

\Theta=sin^{-1}(\frac{1}{\sqrt{5}})

La  calculatrice donne \Theta=0.46

En réalité on obtient :

\Theta=0.46 ou \Theta=\pi-0.46

La solution commune aux deux équations est : \Theta=0.46.

Donc arg(z)=0.46[2\pi].

3. On en déduit la forme trigonométrique

z=\sqrt{5}(cos(0.46)+isin(0.46))

 

En réalité on obtient la forme exponentielle qu’on abordera plus tard qui est de la forme re^{i\Theta} où r est le module et \Theta un argument.

La forme trigonométrique de 2+i est \sqrt{5}(cos(0.46)+isin(0.46))

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.