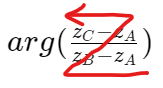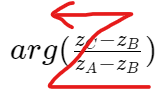Sommaire
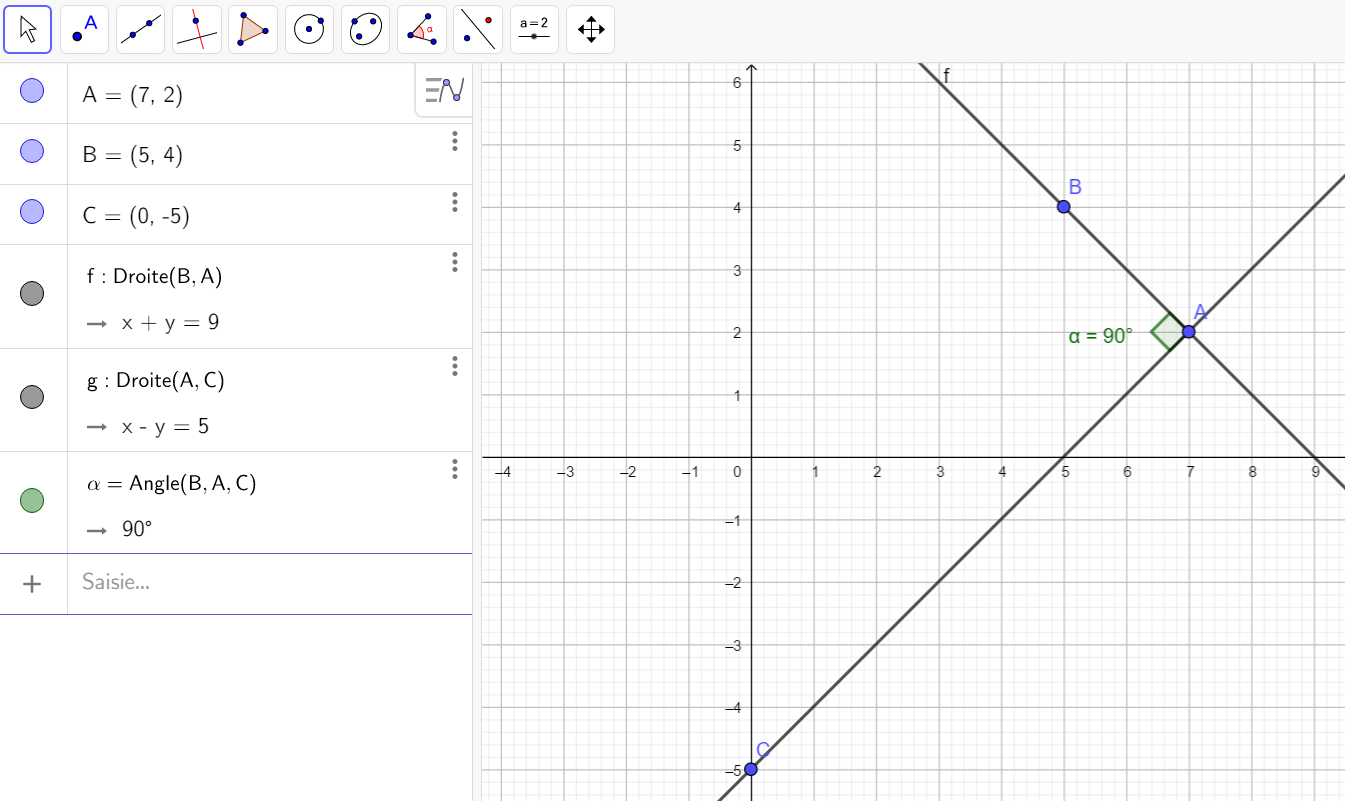
On pourra utiliser cette fenêtre Géogébra pour construire les figures des différents exercices.
Module et argument de b-a
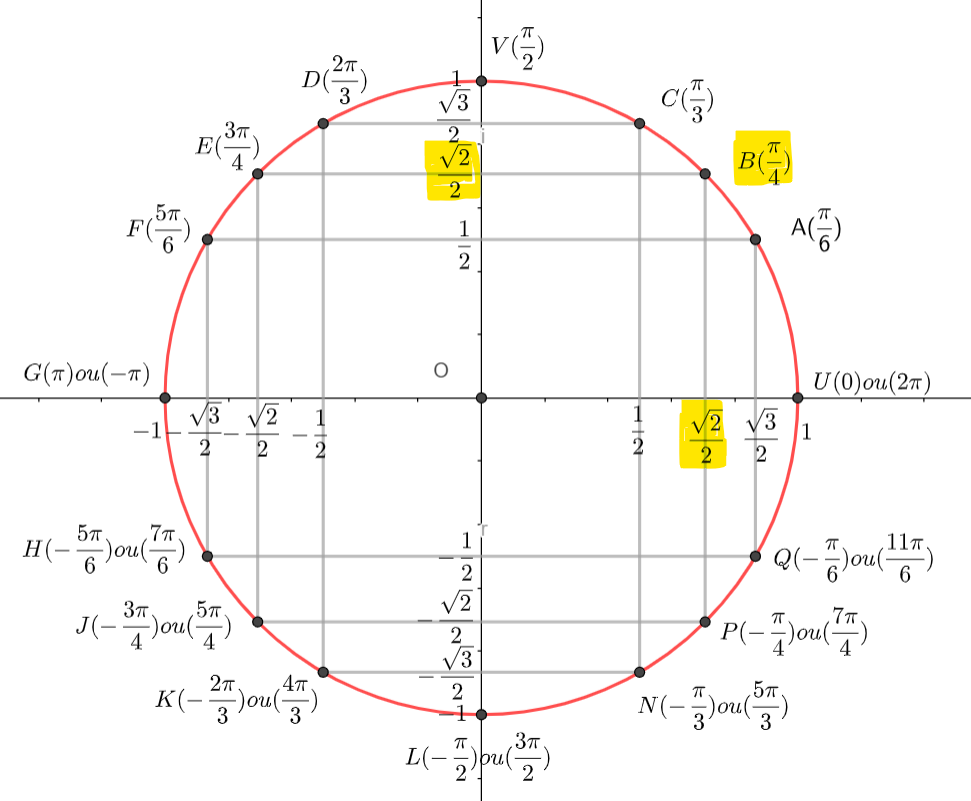
Dans cette fiche, le plan est muni du repère orthonormé (O,U,V).
Propriétés
A et B sont deux points d’affixes respectives a et b. On a :
AB=|b-a| et (\overrightarrow{OU},\overrightarrow{AB})=arg(b-a)[2\pi]
Exercice n°1
Calculer l’affixe du vecteur \overrightarrow{AB} dans chaque cas puis en déduire la longueur AB et l’angle (\overrightarrow{OU},\overrightarrow{AB}).
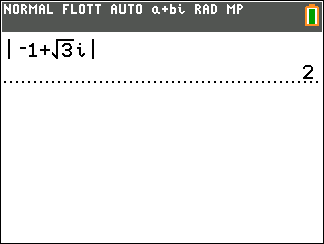
z_A=1+2i et z_B=2+3i
z_A=2+\sqrt{3}i et z_B=1+2\sqrt{3}i
Exercice n°2
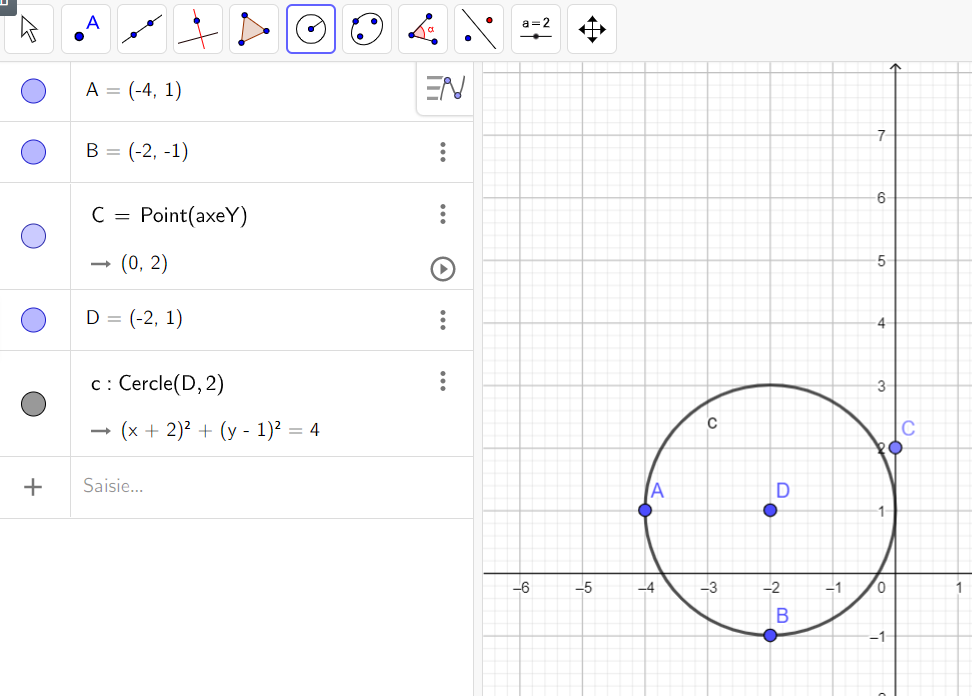
Soient quatre points du plan A,B,C et D d’affixes z_A=-4+i , z_B=-2-i , z_C=2i et z_D=-2+i . Parmi les trois points A,B,C, lequel ne se trouve pas sur le cercle de centre D et de rayon 2 ?
Exercice n°3
Soient quatre points du plan A,B,C et D d’affixes z_A=-3+i , z_B=1+3i , z_C=1-2i et z_D=-2+5i . Parmi les deux points C et D, lequel ne se trouve pas sur la médiatrice de [AB]?
Module et argument de (c-a)/(b-a)
Propriétés
A , B et C sont trois points d’affixes respectives a , b et c avec a\ne b et a\ne c. On a :
\frac{AC}{AB}=\frac{|c-a|}{|b-a|} et (\overrightarrow{AB},\overrightarrow{AC})=arg(\frac{c-a}{b-a})[2\pi]
Démonstration
\frac{AC}{AB}=\frac{|c-a|}{|b-a|}=|\frac{c-a}{b-a}|
(\overrightarrow{AB},\overrightarrow{AC})=(\overrightarrow{AB},\overrightarrow{OU})+(\overrightarrow{OU},\overrightarrow{AC})\\\hspace{1.6cm}=(\overrightarrow{OU},\overrightarrow{AC})-(\overrightarrow{OU},\overrightarrow{AB})\\\hspace{1.6cm}=arg(c-a)-arg(b-a)\\\hspace{1.6cm}=arg(\frac{c-a}{b-a})
Conséquences
A , B et C sont trois points d’affixes respectives a , b et c avec a\ne b et a\ne c.
\frac{|c-a|}{|b-a|}=1 \iff AC=AB
arg(\frac{c-a}{b-a})=0[\pi] \iff A,B,C alignés
arg(\frac{c-a}{b-a})=\frac{\pi}{2}[\pi] \iff (AB) et (AC) sont orthogonales.
Exercice n°4
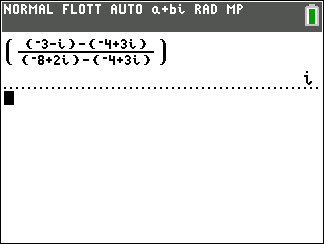
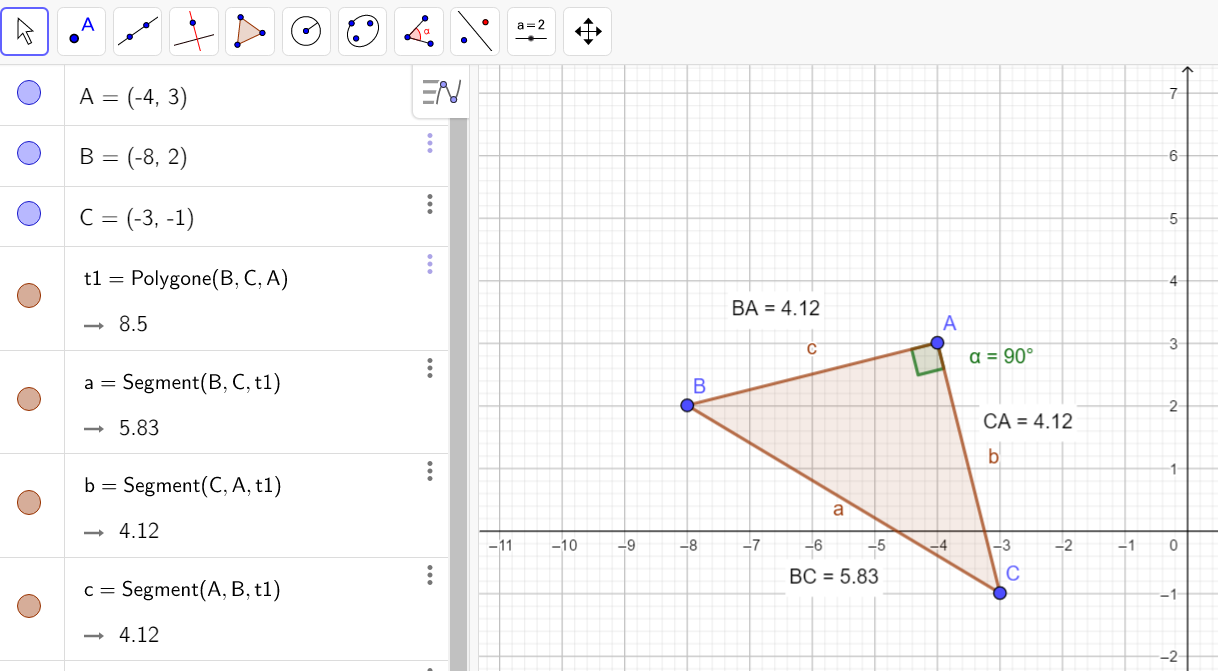
Soient trois points du plan A,B et C d’affixes z_A=-4+3i , z_B=-8+2i et z_C=-3-i.
- Calculer \frac{z_C-z_A}{z_B-z_A}
2. Déterminer |\frac{z_C-z_A}{z_B-z_A}| , en déduire que le triangle ABC est isocèle en B.
3. Déterminer arg(\frac{z_C-z_A}{z_B-z_A}) , en déduire que le triangle ABC est rectangle en B.
Exercice n°5
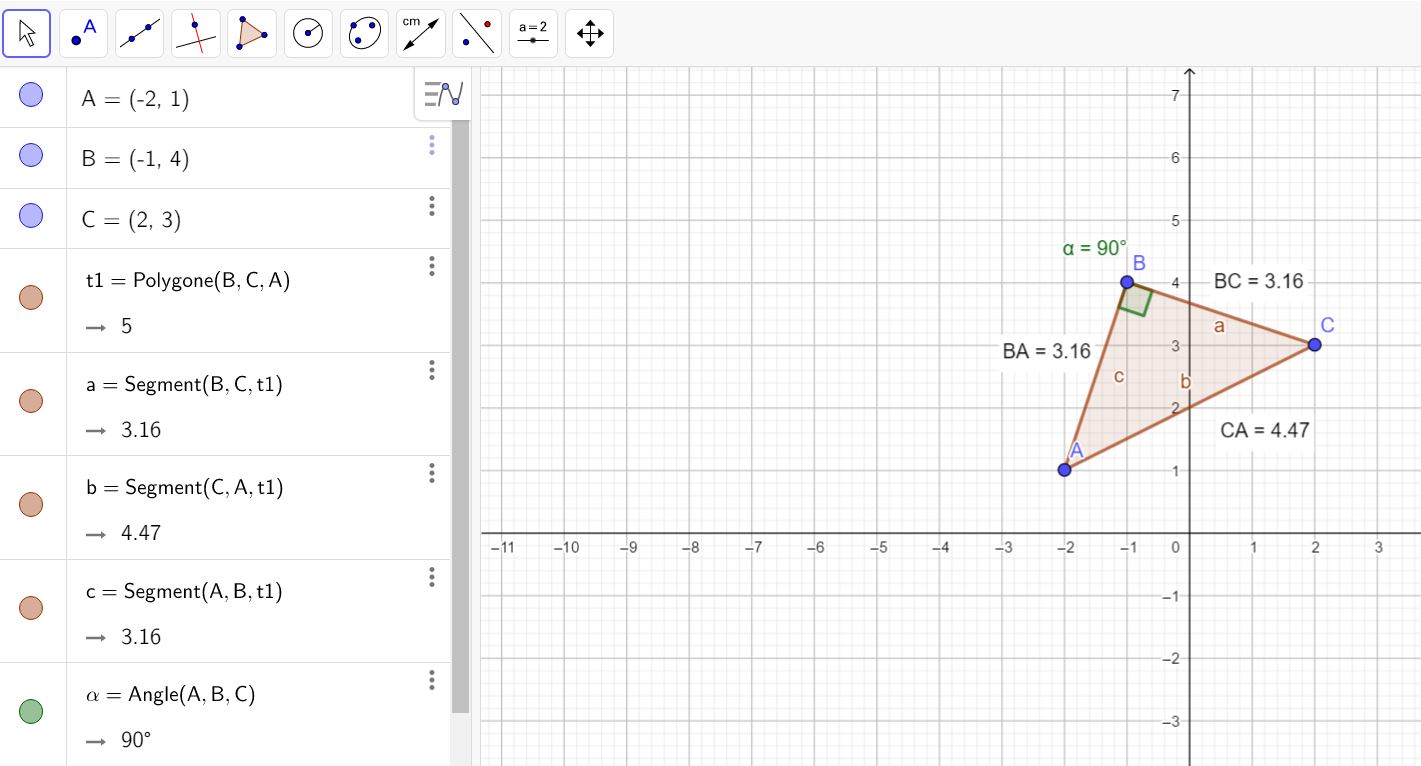
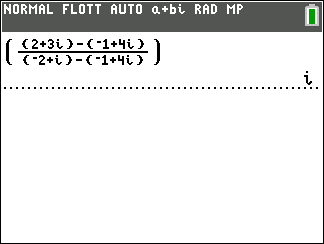
Soient trois points du plan A,B et C d’affixes z_A=-2+i , z_B=-1+4i et z_C=2+3i.
- Calculer \frac{z_C-z_B}{z_A-z_B}
2. Déterminer |\frac{z_C-z_B}{z_A-z_B}| , en déduire que le triangle ABC est isocèle en B.
3. Déterminer arg(\frac{z_C-z_B}{z_A-z_B}) , en déduire que le triangle ABC est rectangle en B.
Exercice n°6
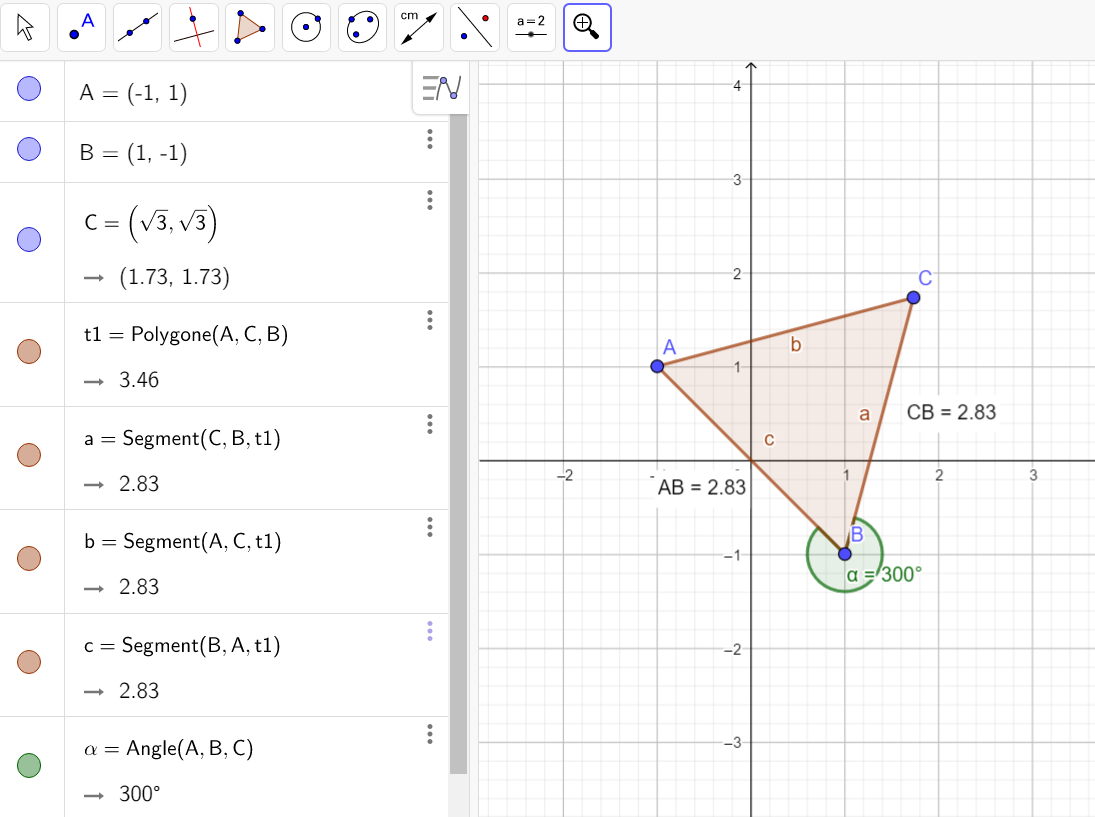
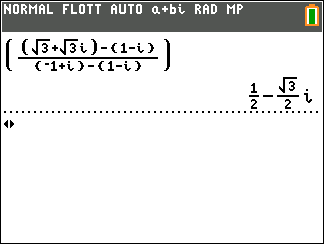
Soient trois points du plan A,B et C d’affixes z_A=-1+i , z_B=1-i et z_C=\sqrt{3}+\sqrt{3}i.
- Calculer \frac{z_C-z_B}{z_A-z_B}
2. Déterminer |\frac{z_C-z_B}{z_A-z_B}| , en déduire que le triangle ABC est isocèle en B.
3. Déterminer arg(\frac{z_C-z_B}{z_A-z_B}) , en déduire que le triangle ABC est équilatéral en B.
Exercice n°7
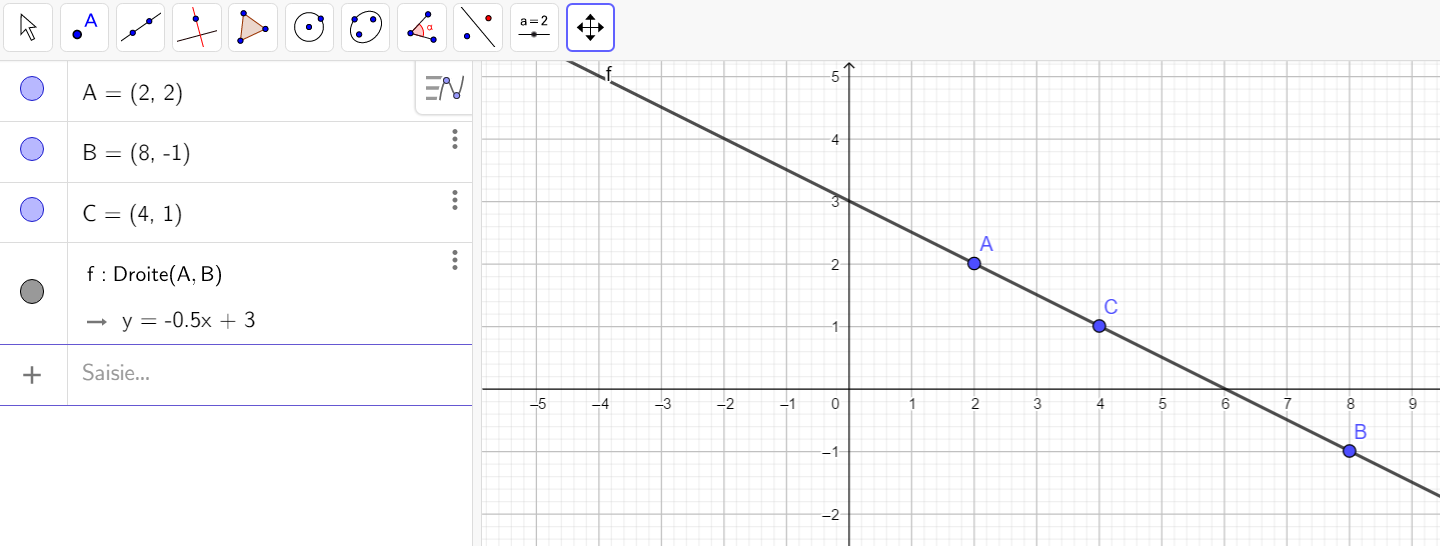
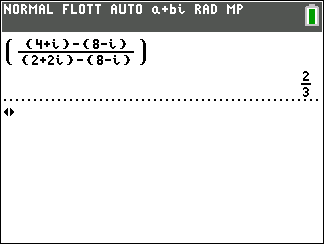
Soient trois points du plan A,B et C d’affixes z_A=2+2i , z_B=8-i et z_C=4+i.
Montrer que les points A,B et C sont alignés.
Exercice n°8
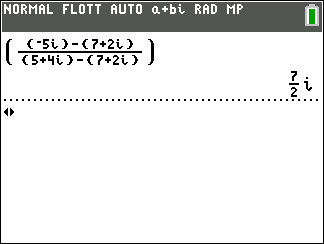
Soient trois points du plan A,B et C d’affixes z_A=7+2i , z_B=5+4i et z_C=-5i.
Montrer que les droites (AB) et (AC) sont orthogonales.