Sommaire
Définition : forme exponentielle d’un nombre complexe
Définition
Tout nombre complexe non nul s’écrit sous la forme z=re^{i\theta} où r est le module de z et \theta un argument de z.
Cette écriture est appelée forme exponentielle de z.
Exemple n°1
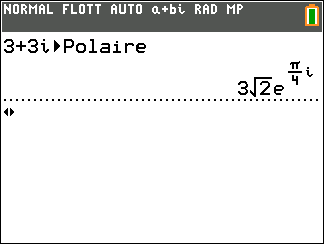
Soit le complexe 2+2i. On a |2+2i|=2\sqrt{2} et arg(2+2i)=\frac{\pi}{4} donc 2+2i=2\sqrt{2}e^{i\frac{\pi}{4}}.
Exemple n°2
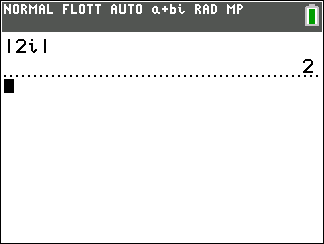
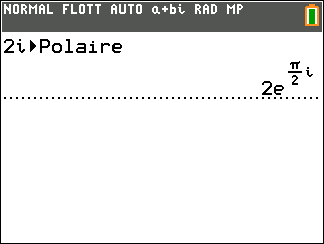
Soit le complexe i. On a |i|=1 et arg(i)=\frac{\pi}{2} donc i=e^{i\frac{\pi}{2}}.
Exercice n°1
Déterminer dans chaque cas le forme exponentielle de z.
Propriétés : calculs avec la forme exponentielle d’un nombre complexe
Propriétés
Pour tous réels \theta et \theta’ , on a
re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}
Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}
Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}
\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}
\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}
Exercice n°2
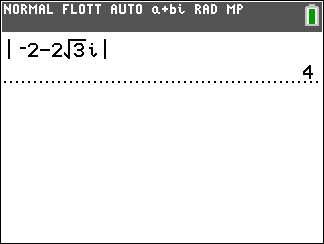
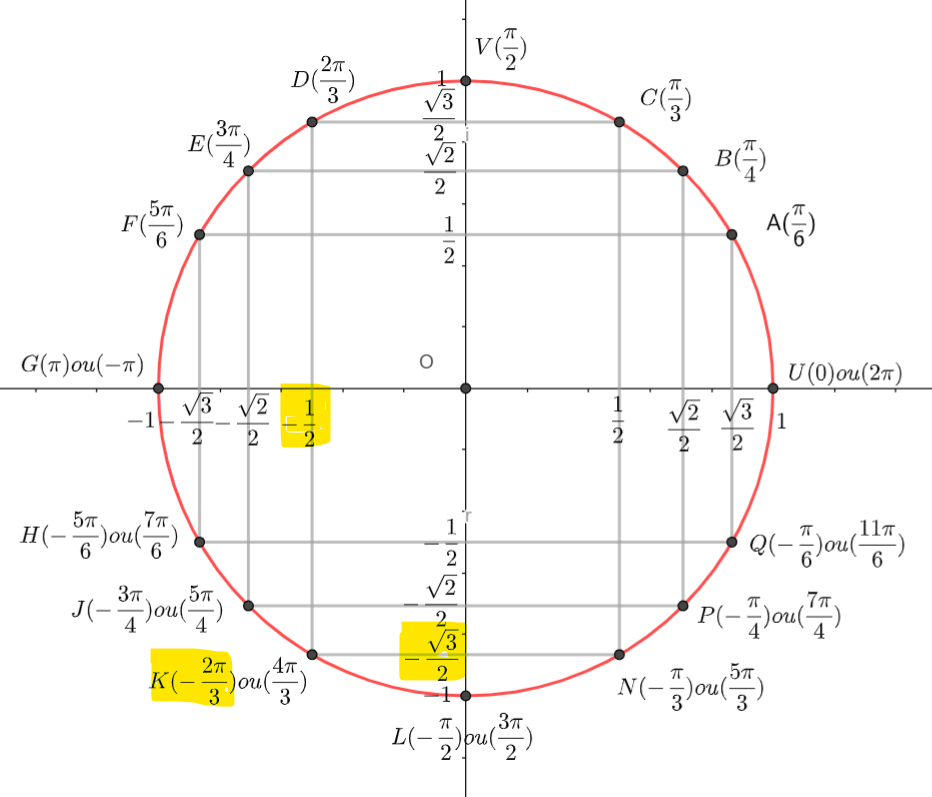
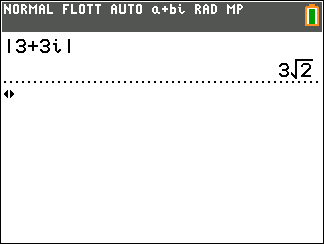
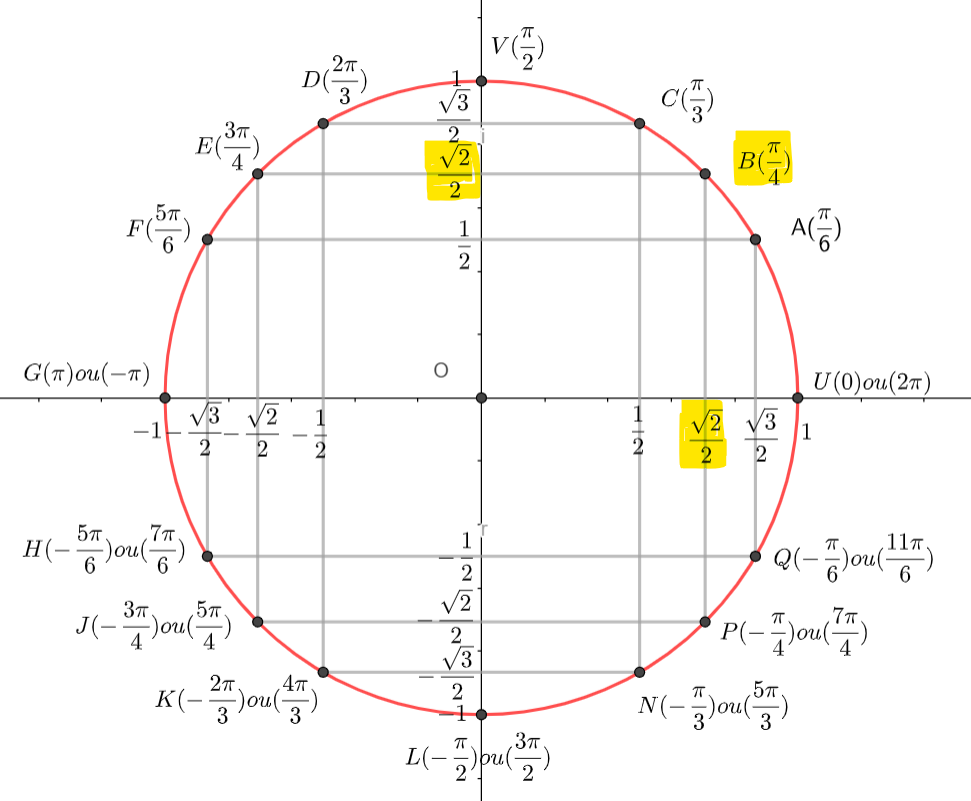
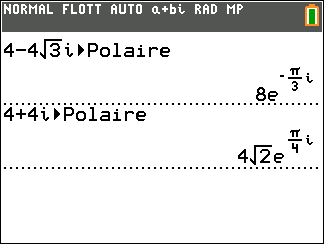
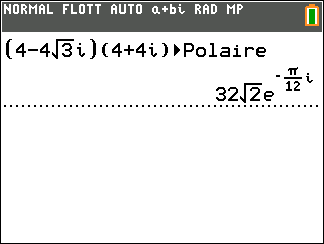
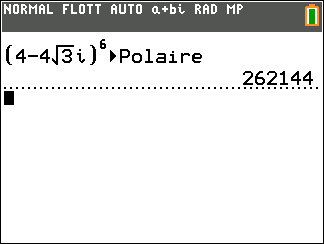
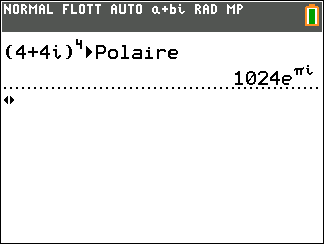
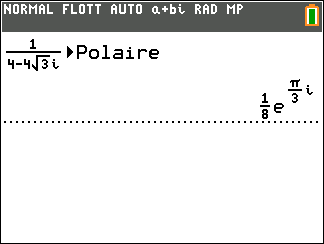
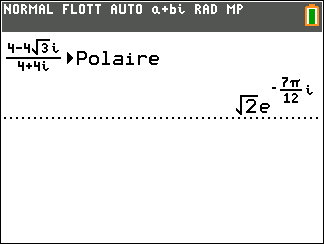
- A l’aide de la calculatrice, déterminer la forme exponentielle de z_1=4-4\sqrt{3}i et de z_2=4+4i
2. En utilisant les propriétés précédentes, déterminer la forme exponentielle dans chaque cas.
Egalité de nombres complexes
Théorème
Soient z=re^{i\Theta} et z’=r’e^{i\Theta’} deux nombres complexes sous forme exponentielle.
z=z’ \iff r=r’ et \theta=\theta'[2\pi]
Formule de Moivre
Théorème
Pour tout \theta \in \mathbf{R} et pour tout n \in \mathbf{Z} ,
(cos(\theta)+isin(\theta))^n=cos(n\theta)+isin(n\theta)
Formules d’Euler
Théorème
Pour tout \theta \in \mathbf{R}
cos(\theta)=\frac{1}{2}(e^{i\theta}+e^{-i\theta}) et sin(\theta)=\frac{1}{2i}(e^{i\theta}-e^{-i\theta})
Exercice n°3
Démontrer que pout tout réel x , cos(2x)sin^2(x)=-\frac{1}{4}cos(4x)+\frac{1}{2}cos(2x)-\frac{1}{4}
Exercice n°4
Démontrer que pout tout réel x , sin(x)cos^2(x)=\frac{sin(3x)+sin(x)}{4}
Exercice n°5
Démontrer que pout tout réel x , cos^3(x)=\frac{cos(3x)+3cos(x)}{4}