logo

TE. Arithmétique : nombres premiers

Nombres premiers

Nombres premiers

Définition 

On dit qu’un nombre entier naturel est premier s’il admet exactement deux diviseurs 1 et lui-même

Remarques

 0 n’est pas premier car il admet une infinité de diviseurs. 

 1 n’est pas premier car il n’admet qu’un seul diviseur. 

 2 est le seul nombre pair premier car les autres nombres pairs ont au moins trois diviseurs : 1 , 2 et eux-mêmes.

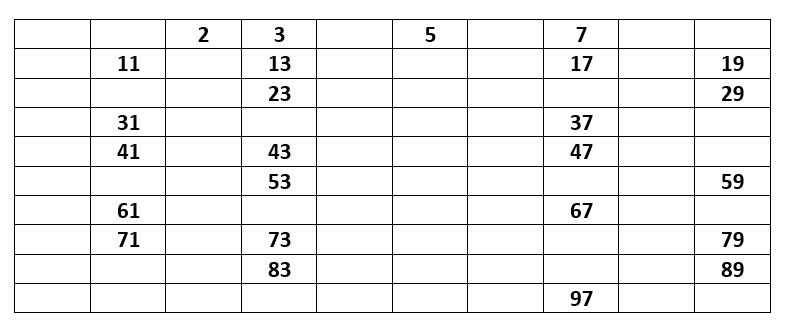
Crible d’Eratosthène pour déterminer les nombres premiers inférieurs à 100.

  1. On supprime le nombre  1, on garde le nombre 2 et on supprime tous les multiples de 2.
  2. On garde le nombre 3 et on supprime tous les multiples de 3.
  3. On garde le nombre 5 et on supprime tous les multiples de 5.
  4. On garde le nombre 7 et on supprime tous les multiples de 7.

Comme \sqrt{100}=10, on s’arrête car sinon on passerait à 11 qui est plus grand que \sqrt{100}=10.

Reconnaissance d’un nombre premier

Propriété

n désigne un nombre entier naturel supérieur ou égal à 4.

Si n n’est pas premier, alors n admet au moins un diviseur premier p son plus petit diviseur autre que  1 tel que 2\leq p \leq \sqrt{n}.

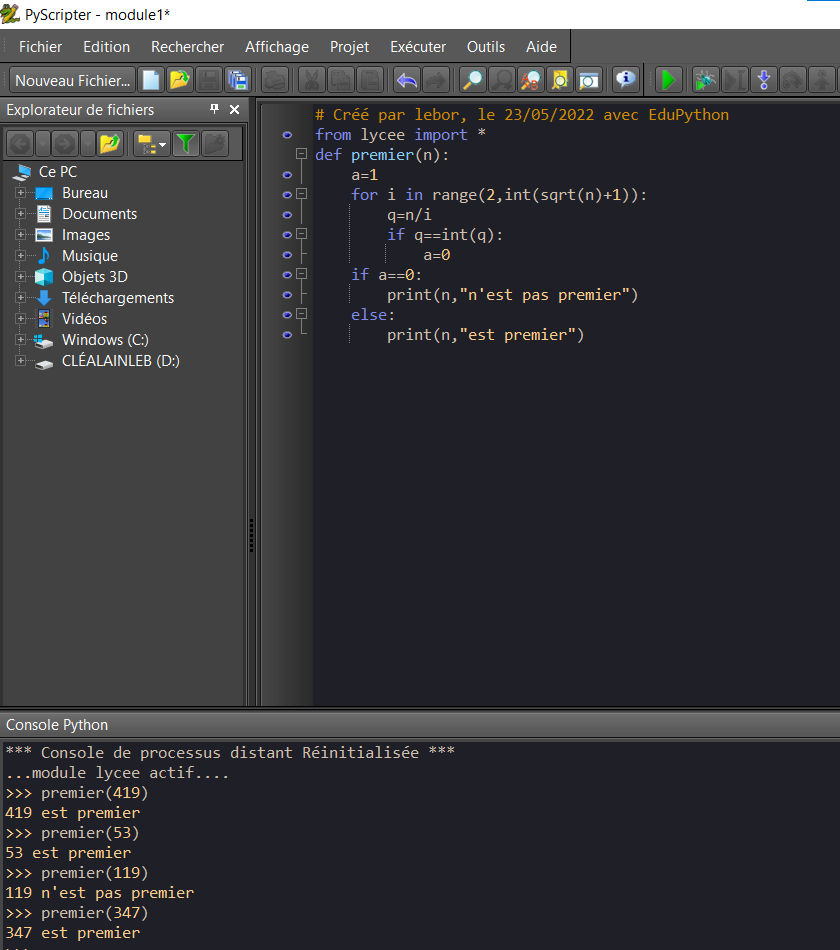
Cliquez ici pour écrire un programme sur la TI 83 Python qui teste si un nombre est premier

Exercice n°1

Les nombres suivants sont-ils premiers ?

419
correction
53
correction
119
correction
347
correction
Je vérifie avec un programme Python

L’ensemble des nombres premiers

Propriété

Il existe une infinité de nombres premiers.

Démonstration

On raisonne par l’absurde, on suppose qu’il existe un nombre fini de nombres premiers, par exemple n que l’on note p_1,p_2,…,p_n.

On considère le nombre p_1p_2…p_n+1. Ce nombre entier est supérieur ou égal à 2, donc il admet au moins un diviseur premier p_i parmi p_1,p_2,…,p_n.

p_i divise p_1p_2…p_n+1 et p_i divise p_1p_2…p_n donc il divise aussi la différence c’est-à-dire 1. Ce qui est impossible.

Donc il existe un nombre infini de nombres entiers.

Exercice n°2

n est un nombre entier naturel supérieur ou égal à 3.

Démontrer que n^2+2n-3 n’est jamais premier.

correction

Exercice n°3

p est un nombre entier naturel au moins égal à 5.

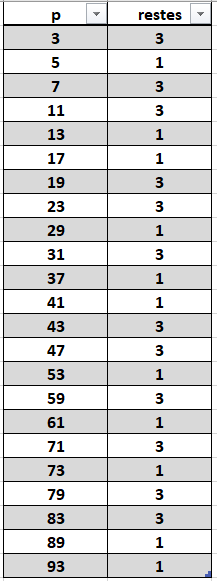
  1. Quels sont les restes possibles dans la division par 12 ?
correction

2. Montrer que p^2+11 est divisible par 12 ?

correction

Exercice n°4

Démontrer que  tout nombre premier supérieur ou égal à 3 est congru à 1 ou -1 modulo 4.

correction

©2020 – Math’O karé SAS

On veut savoir si 419 est premier.

\sqrt{419}\approx 20.47 donc 20<\sqrt{419}<21.

On essaye de diviser 419 par les nombres premiers inférieurs ou égaux à 20, c’est-à-dire 2,3,5,11,13,17 et 19.

419 n’est pas divisible par 2 ( il ne finit pas par 0,2,4,6 ou 8).

419 n’est pas divisible par 3 ( la somme de ses chiffres 4+1+9=14 n’est pas divisible par 3).

419 n’est pas divisible par 5 ( il ne finit pas par 0 ou 5).

419=7\times 59+6 n’est pas divisible par 7 ( le reste de la divsion de 419 par 7 n’est pas égal à 0).

419=11\times 38+1 n’est pas divisible par 11 ( le reste de la divsion de 419 par 11 n’est pas égal à 0).

419=13\times 32+3 n’est pas divisible par 13 ( le reste de la divsion de 419 par 13 n’est pas égal à 0).

419=17\times 24+11 n’est pas divisible par 17 ( le reste de la divsion de 419 par 17 n’est pas égal à 0).

419=19\times 22+1 n’est pas divisible par 19 ( le reste de la divsion de 419 par 19 n’est pas égal à 0).

Il n’y a pas de nombre premier inférieur ou égal à 20 qui divise 419.

Donc 419 est un nombre premier.

On veut savoir si 53 est premier.

\sqrt{53}\approx 7.28 donc 7<\sqrt{53}<8.

On essaye de diviser 53 par les nombres premiers inférieurs ou égaux à 7, c’est-à-dire 2,3,5 et 7.

53 n’est pas divisible par 2 ( il ne finit pas par 0,2,4,6 ou 8).

53 n’est pas divisible par 3 ( la somme de ses chiffres 5+3=8 n’est pas divisible par 3).

53 n’est pas divisible par 5 ( il ne finit pas par 0 ou 5).

53=7\times 7+4 n’est pas divisible par 7 ( le reste de la division de 53 par 7 n’est pas égal à 0).

Il n’y a pas de nombre premier inférieur ou égal à 7 qui divise 53.

Donc, d’après la propriété, 53 est un nombre premier.

On veut savoir si 119 est premier.

\sqrt{119}\approx 10.91 donc 10<\sqrt{119}<11.

On essaye de diviser 119 par les nombres premiers inférieurs ou égaux à 10, c’est-à-dire 2,3,5 et 7.

119 n’est pas divisible par 2 ( il ne finit pas par 0,2,4,6 ou 8).

119 n’est pas divisible par 3 ( la somme de ses chiffres 1+1+9=11 n’est pas divisible par 3).

119 n’est pas divisible par 5 ( il ne finit pas par 0 ou 5).

119=7\times 17 est divisible par 7 ( le reste de la division de 119 par 7 est égal à 0).

Il y a donc un nombre premier inférieur ou égal à 10 autre que 1 qui divise 119, c’est 7.

Donc 119 n’est pas un nombre premier.

On veut savoir si 347 est premier.

\sqrt{347}\approx 18.63 donc 18<\sqrt{419}<19.

On essaye de diviser 347 par les nombres premiers inférieurs ou égaux à 18, c’est-à-dire 2,3,5,11,13 et 17.

347 n’est pas divisible par 2 ( il ne finit pas par 0,2,4,6 ou 8).

347 n’est pas divisible par 3 ( la somme de ses chiffres 3+4+7=14 n’est pas divisible par 3).

347 n’est pas divisible par 5 ( il ne finit pas par 0 ou 5).

347=7\times 49+4 n’est pas divisible par 7 ( le reste de la divsion de 347 par 7 n’est pas égal à 0).

347=11\times 31+6 n’est pas divisible par 13 ( le reste de la divsion de 347 par 11 n’est pas égal à 0).

347=13\times 26+9 n’est pas divisible par 13 ( le reste de la divsion de 347 par 13 n’est pas égal à 0).

347=17\times 20+7 n’est pas divisible par 17 ( le reste de la divsion de 347 par 17 n’est pas égal à 0).

Il n’y a pas de nombre premier inférieur ou égal à 18 qui divise 347.

Donc 347 est un nombre premier.

n est un nombre entier naturel supérieur ou égal à 3.

On veut montrer que n^2+2n-3 n’est jamais premier.

Il faut montrer qu’il admet plus que deux diviseurs.

On se propose de factoriser n^2+2n-3.

Méthode n°1 :

n^2+2n est le début du développement n^2+2n+1 c’est-à-dire (n+1)^2.

n^2+2n=(n+1)^2-1

On enlève 3 de chaque côté.

n^2+2n-3=(n+1)^2-1-3

n^2+2n-3=(n+1)^2-4

On factorise le membre de droite avec l’identité remarquable a^2-b^2=(a-b)(a+b).

n^2+2n-3=(n+1)^2-2^2

n^2+2n-3=(n+1-2)(n+1+2)

n^2+2n-3=(n-1)(n+3)

Méthode n°2 :

1.Calcul de \Delta=b²-4ac

J’identifie les coefficients  a=1, b=2 et c=-3.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,2, (-3)  .

\Delta=2²-4\times{1}\times{(-3)}\\\Delta=4+12\\\Delta=16

2.J’applique le théorème :

comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}

et le polynôme se factorise ainsi

ax^2+bx+c=a(x-x_1)(x-x_2)

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, 2  , 16.

x_1=\frac{-2-\sqrt{16}}{2\times{1}}\\x_1=\frac{-2-4}{2}\\x_1=\frac{-6}{2}\\x_1=-3

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, 2 , 16.

x_2=\frac{-2+\sqrt{16}}{2\times{1}}\\x_2=\frac{-2+4}{2}\\x_2=\frac{2}{2}\\x_2=1

Je conclus :

n^2+2n-3=1(n-(-3))(n-1)\\n^2+2n-3=(n+3)(n-1)

Quelle que soit la méthode, on obtient n^2+2n-3=(n+3)(n-1) , donc n^2+2n-3 admet quatre diviseurs : 1 , n-1 et n^2+2n-3 .

Donc n^2+2n-3 n’est jamais premier.

 

 

Voici un tableau EXCEL à deux colonnes, la première contient des nombres premiers au moins égaux à 5 et la deuxième contient les restes de la division par 12 des nombres de la première colonne.

Pour compléter la deuxième colonne, on saisit dans la première cellule =MOD(A1;12) qui permet d’afficher le reste de la division du nombre de la cellule A1 par 12.

                            p                                         restes

55
77
1111
131
175
197
2311
295
317
371
415
437
4711
535
5911
611
7111
731
797
8311
895
971

On ne peut pas avoir pour restes 0,2,4,6,8 car si on a 

0 pour reste, p=12k+0 et donc p est divisible par 2, ce qui est impossible car p est premier.

2 pour reste, p=12k+2 et donc p est divisible par 2, ce qui est impossible car p est premier.

…

On ne peut pas avoir pour reste 3 car si on a 3 pour reste, p=12k+3=3(4k+1) et donc p est divisible par 3, ce qui est impossible car p est premier.

Les restes possibles sont : 1,5,7,11 .

 

Voici un tableau EXCEL à cinq colonnes, la première contient des nombres premiers au moins égaux à 5, la deuxième contient les restes de la division par 12 des nombres de la première colonne, la 3ème contient les carrés des nombres premiers, la 4ème contient les carrés des nombres premiers augmentés de 11 et la dernière contient les restes de la division par 12 des nombres de la quatrième colonne.

Pour compléter la deuxième colonne, on saisit dans la première cellule =MOD(A1;12) qui permet d’afficher le reste de la division du nombre de la cellule A1 par 12.

Pour compléter la 5ème colonne, on saisit dans la première cellule =MOD(A4;12) qui permet d’afficher le reste de la division du nombre de la cellule A4 par 12.

         p         restes                p²                     p²+11        restes

5525360
7749600
11111211320
1311691800
1752893000
1973613720
23115295400
2958418520
3179619720
371136913800
415168116920
437184918600
4711220922200
535280928200
5911348134920
611372137320
7111504150520
731532953400
797624162520
8311688969000
895792179320
971940994200

On peut conjecturer à l’aide du tableau que p^2+11 est divisible par  12.

On va utiliser le résultat de la question 1 et examiner tous les cas.

cas n°1

p\equiv1[12]\\p^2\equiv1^2[12]\\p^2\equiv1[12]\\p^2+11\equiv1+11[12]\\p^2+11\equiv12[12]\\p^2+11\equiv0[12]

Donc p^2+11 est divisible par 12

cas n°2

p\equiv5[12]\\p^2\equiv5^2[12]\\p^2\equiv25[12] et comme 25\equiv1[12]\\p^2\equiv1[12]\\p^2+11\equiv1+11[12]\\p^2+11\equiv12[12]\\p^2+11\equiv0[12]

Donc p^2+11 est divisible par 12

cas n°3

p\equiv7[12]\\p^2\equiv7^2[12]\\p^2\equiv49[12] et comme 49\equiv1[12]\\p^2\equiv1[12]\\p^2+11\equiv1+11[12]\\p^2+11\equiv12[12]\\p^2+11\equiv0[12]

Donc p^2+11 est divisible par 12

cas n°4

p\equiv11[12]\\p^2\equiv11^2[12]\\p^2\equiv121[12] et comme 121\equiv1[12]\\p^2\equiv1[12]\\p^2+11\equiv1+11[12]\\p^2+11\equiv12[12]\\p^2+11\equiv0[12]

Donc p^2+11 est divisible par 12

On a donc montré que p^2+11 est divisible par  12 pour p premier au moins égal à 5.

 

 

Voici un tableau EXCEL à deux colonnes, la première contient des nombres premiers au moins égaux à 3, la deuxième contient les restes de la division par 4 des nombres de la première colonne.

Pour compléter la deuxième colonne, on saisit dans la première cellule =MOD(A2;4) qui permet d’afficher le reste de la division du nombre de la cellule A2 par 4.

On peut conjecturer à l’aide du tableau que p\equiv1[4] ou p\equiv{3}[4].

Comme 3\equiv{-1}[4], on peut conjecturer que 

p\equiv1[4] ou p\equiv{-1}[4].

Les restes de la division par 4 sont 0,1,2,3.

On ne peut pas avoir 0 pour reste sinon p=4k+0 et il est donc divisible par 4 ce qui est impossible car il est premier.

On ne peut pas avoir 2 pour reste sinon p=4k+2=2(2k+1) et il est donc divisible par 2 ce qui est impossible car il est premier.

Donc p\equiv1[4] ou p\equiv{-1}[4].

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.