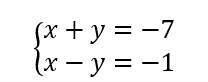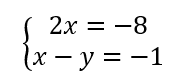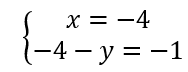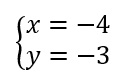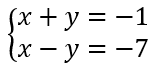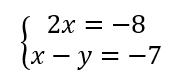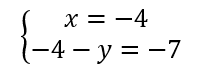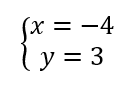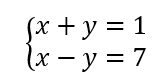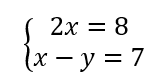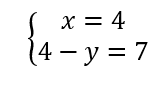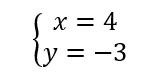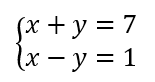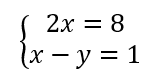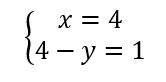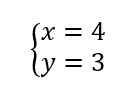Multiples et diviseurs d’un nombre entier relatif
Définition
a et b sont des nombres entiers relatifs.
On dit que a divise b s’il existe un nombre entier relatif k tel que b=k\times a
Exemples
7 divise -21 car -21=(-3)\times 7\\n-7 divise n^2-49 car n^2-49=(n-7)\times (n+7)
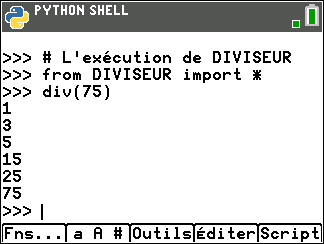
Exercice n°1
Déterminer l’ensemble des diviseurs de 75 dans \mathbf{Z}.
Propriétés de la divisibilité dans Z
Définition
a , b et c sont des nombres entiers relatifs.
Si a divise b et c alors a divise b+c et b-c et plus généralement a divise bu+cv où u et v sont des entiers relatifs.
Démonstration
a divise b donc il existe un entier relatif k tel que b=k\times a
On multiplie par u et on obtient
bu=bk\times a\\a divise c donc il existe un entier relatif k’ tel que c=k’\times a.
On multiplie par v et on obtient
cv=ck’\times aOn ajoute les deux nouvelles égalités
bu+cv=bk\times a+ck’\times a\\bu+cv=(bk+ck’)\times aDonc a divise bu+cv
Exemple n°1
Déterminer les nombres entiers relatifs n tels que n-1 divise n+5.
- Si n-1 divise n+5, comme n-1 divise n-1 alors n-1 divise toute combinaison linéaire de n+5 divise n-1.
En particulier, n-1 divise (n+5)-(n-1) d’où n-1 divise 6.
2. Réciproquement, si n-1 divise 6, comme n-1 divise n-1, alors n-1 divise n-1+6 donc n-1 divise n+5.
3. Conclusion, chercher les entiers relatifs n tels que n-1 divise n+5 équivaut à chercher les entiers relatifs n tels que n-1 divise 6.
Les diviseurs de 6 sont -6;-3;-2;-1;1;2;3;6.
On pourrait résoudre n-1=-6, n-1=-3, …
Les nombres relatifs cherchés sont donc -5;-2;-1;0;2;3;4;5
Exercice n°2
Déterminer les nombres entiers relatifs n tels que n+1 divise n+7.
Exemple n°2
Déterminer les nombres entiers relatifs x et y tels que x^2-y^2=5.
On peut factoriser :
(x-y)(x+y)=5Les diviseurs de 5 sont -5;-1;1:5.
On résout alors les quatre systèmes d’équations :
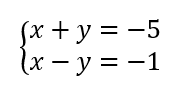
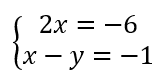
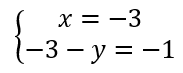
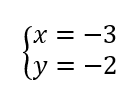
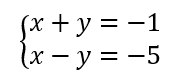
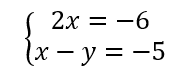
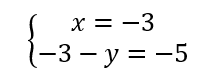
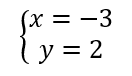
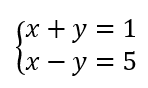
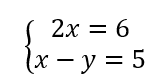
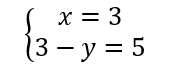
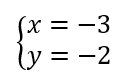
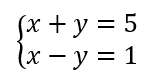
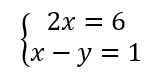
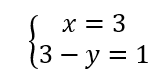
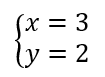
Les couples solutions sont : (-3;-2);(-3;2);(-3;-2);(3;2).
Exercice n°3
Déterminer les nombres entiers relatifs x et y tels que x^2-y^2=7.
Exercice n°4
n désigne un entier naturel, on pose A=n^4-1
Démontrer que n-1,n+1,n^2+1 sont des diviseurs de A=n^4-1.
Exercice n°5
k désigne un entier naturel, on pose a=9k+2 et b=12k+1.
- calculer 4a-3b.
2 En déduire que les seuls diviseurs positifs possibles et communs à a et b sont 1 et 5 .
Exercice n°6
n est un entier relatif tel que n-4 est divisible par 5.
Démontrer que n^2-1 est également divisible par 5.