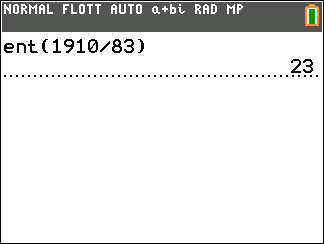
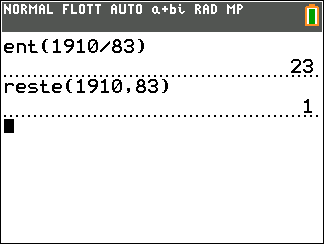
Théorème
Soient a un entier relatif et b un entier naturel non nul.
Il existe un couple d’entiers relatifs (q;r) tels que a=bq+r et 0\leq r<b.
q est le quotient et r est le reste de la division de a par b.
Exemples
- 117=28\times 4+5 représente la division de 117 par 28 avec un quotient égal à 28 et le reste égal à 5. Cette écriture ne peut pas représenter la division de 117 par 4 car le reste égal à 5 serait plus grand que le diviseur 4.
- 95=3\times 31+2 représente la division de 95 par 3 avec un quotient égal à 31 et le reste égal à 2. Cette écriture peut aussi représenter la division de 95 par 31 avec un quotient égal à 3 et le reste égal à 2.
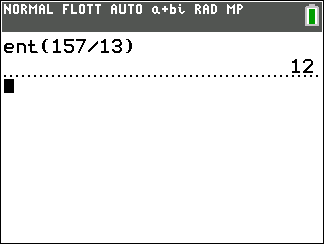
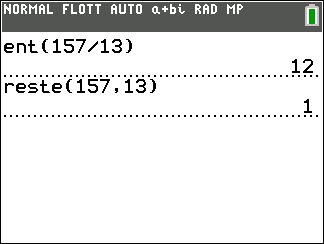
Déterminer le reste et le quotient d’une division euclidienne avec Edupython
Ecrire le programme suivant, l’instruction a%b représente la division de a par b
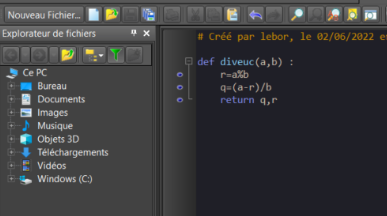
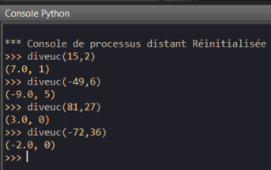
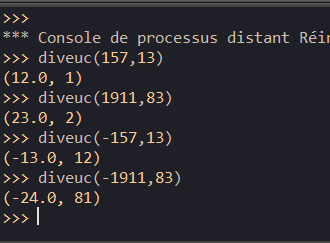
On obtient donc
Dans la division de 15 par 2 le quotient est égal à 7 et le reste est égal à 1. Donc 15=2\times 7+1.
Dans la division de -49 par 6 le quotient est égal à -9 et le reste est égal à 5. Donc -49=6\times (-9)+5.
Dans la division de 81 par 27 le quotient est égal à 3 et le reste est égal à 0. Donc 81=27\times 3+0 ou
81=27\times 3.
Dans la division de -72 par 36 le quotient est égal à -2 et le reste est égal à 0. Donc -72=36\times (-2)+0 ou -72=36\times (-2).
Exercice n°1
Dans chaque cas, effectuer la division euclidienne de a par b.
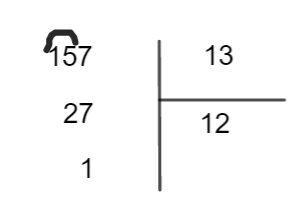
a=157 et b=13.
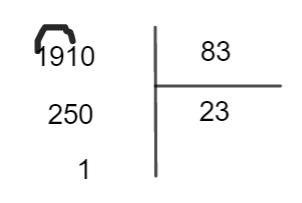
a=1910 et b=83.
a=-157 et b=13.
a=-1910 et b=83.
Exercice n°2
n désigne un nombre entier naturel.
On pose A=n(n^2+5).
Démontrer que, pour tout entier n , A est divisible par 3.
Exercice n°3
Par quel entier n faut-il diviser 1088 pour obtenir 37 comme quotient et 15 pour reste.
Exercice n°4
Indiquer si les égalités suivantes correspondent à une ou deux divisions euclidiennes. Préciser alors le quotient et le reste.