PGCD de deux entiers naturels
Définition
Soient a et b deux entiers naturels non tous les deux nuls.
On note D(a;b) l’ensemble des diviseurs communs de a et b.
L’ensemble D(a;b) contient un plus grand élément, noté PGCD(a;b). C’est le plus grand diviseur commun de de a et b.
Exemples
D(12;20)=\{-4;-2;-1;1;2;4\} donc PGCD(12;20)=4.
D(6;15)=\{-3;-1;1;3\} donc PGCD(6;15)=3.
Déterminer le PGCD avec la TI 83 Premium CE Python
Au clavier
A l’écran
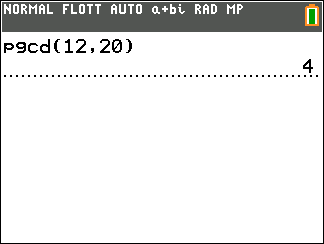
Appuyer sur la touche math, sélectionner la colonne NBRE et sélectionner 9: pgcd( dans le menu déroulant.
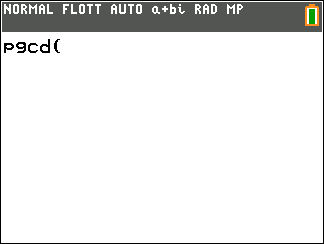
Saisir les deux nombres, par exemple 12 et 20 puis valider par entrer.
Exercice n°1
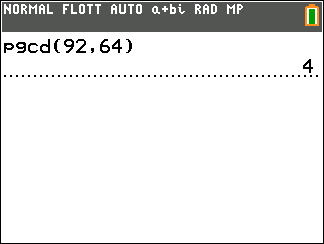
1. Déterminer les diviseurs de 92 et de 64 dans \mathbf{Z}.
2. En déduire le PGCD de 92 et de 64.
Exercice n°2
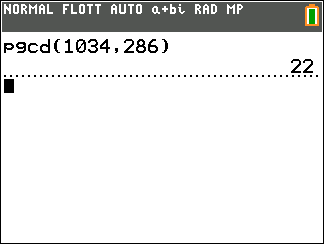
1. Déterminer les diviseurs de 286 dans \mathbf{Z}.
2. En déduire le PGCD de 286 et de 1034.
Algorithme d’Euclide
Soient a et b deux entiers naturels non nuls.
L’algorithme d’Euclide consiste à effectuer la division de a par b puis successivement les divisions du diviseur par le reste de la ligne précédente. A un moment le reste est nul et le PGCD sera le dernier reste non nul.
Voici un exemple où on cherche le PGCD(12;20). Le dernier reste non nul est 4 donc PGCD(20;12)=4

Voici un autre exemple où on cherche le PGCD(42;36). Le dernier reste non nul est 6 donc PGCD(42;36)=6

Exercice n°3
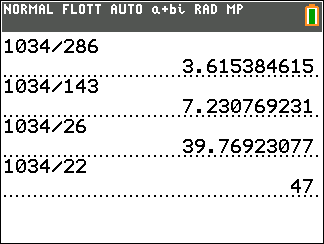
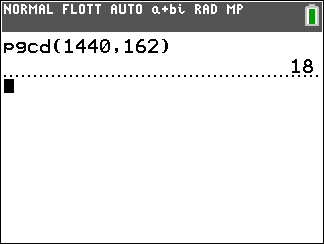
A l’aide de l’algorithme d’Euclide, déterminer le PGCD de 1440 et 162.
Exercice n°4
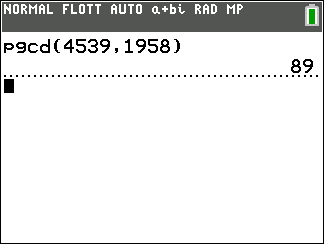
A l’aide de l’algorithme d’Euclide, déterminer le PGCD de 4539 et 1958.
Exercice n°5
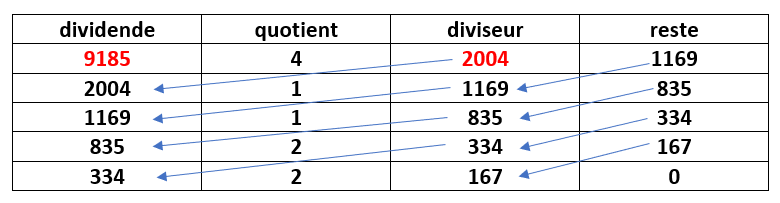
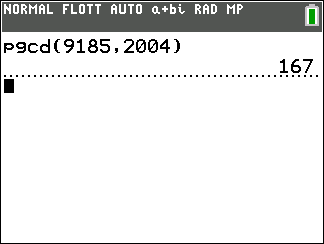
A l’aide de l’algorithme d’Euclide, déterminer le PGCD de 9185 et 2004.