Sommaire
Nombres premiers entre eux
Définition
Soient a et b deux entiers relatifs non nuls.
a et b sont premiers entre eux signifie que PGCD(a;b)=1.
Exemple
6 et 25 sont premiers entre eux car PGCD(6;25)=1.
Propriété
Soient a et b deux entiers relatifs non nuls.
Si PGCD(a;b)=d, alors il existe deux entiers a’ et b’ tels que a=da’ et b=db’ et PGCD(a’;b’)=1.
Exemple
On a PGCD(12;50)=2. De plus 12=2\times 6 et 50=2\times 25 et PGCD(6;25)=1.
Exercice n°1
Déterminer les diviseurs positifs de 1237 et de -120 et indiquer si 1237 et -120 sont premiers entre eux.
Exercice n°2
Déterminer les diviseurs positifs de 1286 et de 1070 et indiquer si 1286 et 1070 sont premiers entre eux.
Exercice n°3
n désigne un nombre entier naturel tel que n\geq 2.
On pose : a=n^2+2n-3 et b=n^2+4n+3.
- Factoriser a=n^2+2n-3 et b=n^2+4n+3.
2. Déterminer PGCD(n-1;n+1) en distinguant les cas n pair et n impair.
3. Exprimer alors PGCD(a;b) en fonction de n.
Identité de Bezout
Identité de Bezout
Soient a et b deux entiers relatifs non nuls.
Si PGCD(a;b)=d alors il existe deux entiers u et v tels que au+bv=d.
Exemple
- Déterminer PGCD(58;24) à l’aide de la calculatrice.
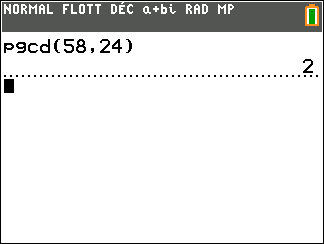
2. En déduire un couple d’entiers relatifs (x;y) tel que 58x-24y=2.
Comme le PGCD(58;24)=2 alors il existe un couple d’entiers relatifs (x;y) tel que 58x-24y=2.
On écrit l’algorithme d’Euclide en rajoutant une colonne.

On écrit la dernière égalité de la dernière colonne :
2=10-2\times 4On remplace 4 par 24-2\times 10
2=10-2\times (24-2\times 10)
On développe
2=10-2\times 24+4\times 10
On réduit
2=5\times 10-2\times 24
On remplace 10 par 58-2\times 24
2=5\times (58-2\times 24)-2\times 24On développe
2=5\times 58-10\times 24-2\times 24
On réduit
2=5\times 58-12\times 24
Donc x=58 et y=12.
Le couple cherché est (58;12).
Exercice n°4
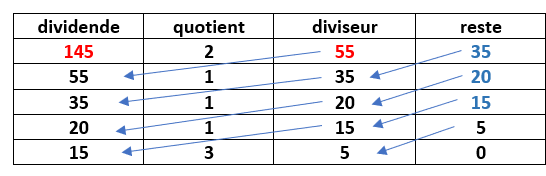
On donne a=145 et b=55
1. Déterminer le PGCD(a;b) avec l’algorithme d’Euclide.
2. En déduire un couple d’entiers relatifs (u;v) tel que au+bv=PGCD(a;b).
Exercice n°5
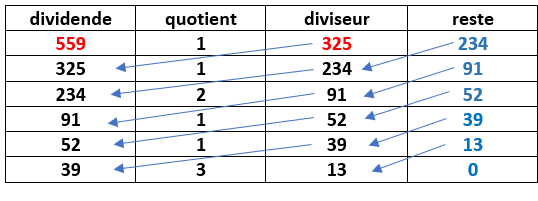
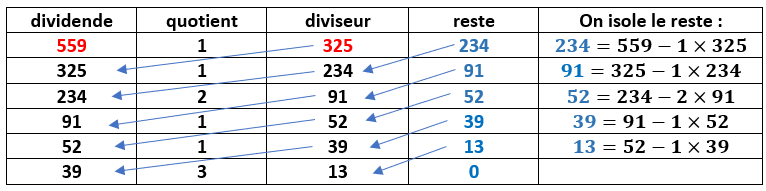
1. Déterminer le PGCD(559;325) avec l’algorithme d’Euclide.
2. En déduire qu’il existe un couple d’entiers relatifs (u;v) tel que 559u+325v=13 et le déterminer.
Exercice n°6
1. Déterminer le PGCD(564;235) avec l’algorithme d’Euclide.
2. En déduire qu’il existe un couple d’entiers relatifs (u;v) tel que 564u+235v=47 et le déterminer.
Théorème de Bezout
Théorème de Bezout
Soient a et b deux entiers relatifs non nuls.
a et b sont premiers entre eux si et seulement si il existe deux entiers u et v tels que au+bv=1.
Déterminer u et v à l’aide de la TI 83 Premium CE
Déterminer u et v tels que 28u-33v=1.
On exprime une des deux inconnues, par exemple v en fonction de u.
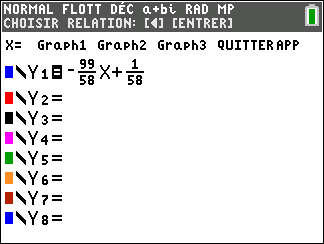
v=\frac{28}{33}u-\frac{1}{33}.
Au clavier
A l’écran
Appuyer sur la touche f(x) puis saisir à côté de Y1 , \frac{28}{33}x-\frac{1}{33}. Valider avec entrer.
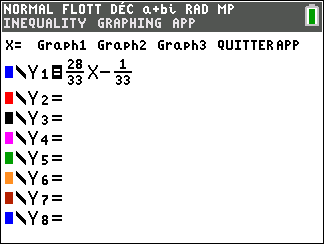
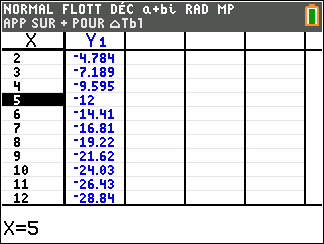
Appuyer sur la touche 2nde puis la touche graphe. Au besoin paramétrer le tableur : 2nde fenêtre, DébutTBL=0 et Tbl=1.
Puis chercher la première valeur entière dans la seconde colonne en parcourant le tableur.
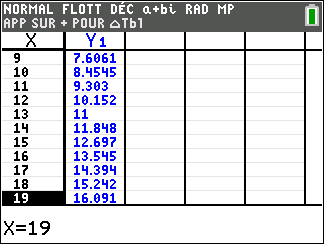
On peut conclure :
A l’aide de la calculatrice u=13 et v=11.
Exercice n°7
- A l’aide de la calculatrice, déterminer deux entiers u et v tels que 99u+58v=1.
2. En déduire le PGCD(99;58).
Exercice n°8
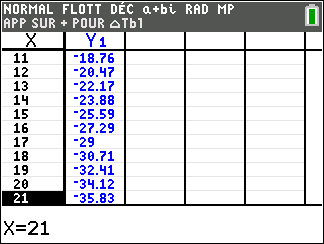
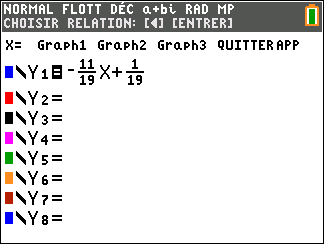
- A l’aide de la calculatrice, déterminer deux entiers u et v tels que 11u+19v=1.
2. En déduire le PGCD(11;19).
Exercice n°9
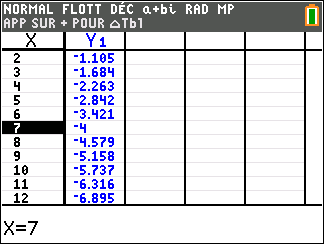
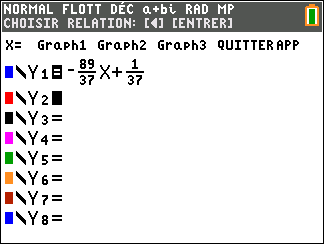
- A l’aide de la calculatrice, déterminer deux entiers x et y tels que 89x+37y=1.
2. En déduire le PGCD(89;37).
Déterminer u et v à l’aide de l’algorithme d’Euclide
Déterminer u et v tels que 38u+15v=1.
On écrit l’algorithme d’Euclide en rajoutant une colonne.

On écrit la dernière égalité de la dernière colonne :
1=8-1\times 7On remplace 7 par 15-1\times 8
1=8-1\times (15-1\times 8)
On réduit
1=8-15+8
1=2\times 8-15
On remplace 8 par 38-2\times 15
1=2\times (38-2\times 15)-15
On développe
1=2\times 38-4\times 15-15
On réduit
1=2\times 38-5\times 15
Donc u=38 et v=-5
Exercice n°10
- A l’aide de l’algorithme d’Euclide, déterminer deux entiers x et y tels que 29x+12y=1.
2. En déduire le PGCD(29;12).
Exercice n°11
- A l’aide de l’algorithme d’Euclide, déterminer deux entiers u et v tels que 31u+70v=1.
2. En déduire le PGCD(31;70).
Exercice n°12
- A l’aide de l’algorithme d’Euclide, déterminer deux entiers u et v tels que 27u+11v=1.
2. En déduire le PGCD(27;11).