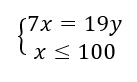TE. Théorème de Gauss.

Arithmétique, Niveau maths expertes, PGCD et théorèmes de Gauss et de Bezout

Théorème de Gauss

Soient $a$ , $b$ et $c$ trois entiers relatifs non nuls.

Si $a$ divise $bc$ et $c$ et si $a$ et $b$ sont premiers entre eux alors $a$ divise $c$

Exemple n°1

On veut résoudre l’équation suivante $23x=7y$ .

Comme $PGCD(23;7)=1$ , les nombres $23$ et $7$ sont premiers entre eux.

Et comme $23$ divise $7y$

D’après le théorème de Gauss, $23$ divise $y$ .

Donc il existe un entier relatif $k$ tel que $y=23k$ .

On remplace $y$ par $23k$ dans $23x=7y$ .

23x=7\times 23k\\x=7k

Les couples solutions sont de la forme $(7k;23k)$ avec $k\in \mathbf{Z}$ .

On s’assure que les solutions trouvées sont bien solutions de l’équation $23x=7y$ .

L’égalité $23\times 7k=7\times 23k$ est bien vérifiée.

Exemple n°2

On veut résoudre l’équation suivante $12x=15y$ .

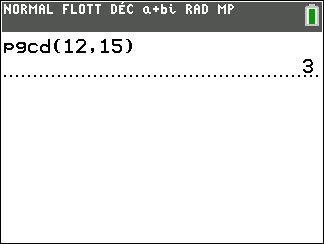
Comme $PGCD(12;15)=3$ , on divise l’équation par $3$ .

\frac{12x}{3}=\frac{15y}{3}\\4x=5y

Les nombres $4$ et $5$ sont premiers entre eux.

De plus $4$ divise $5y$

D’après le théorème de Gauss, $4$ divise $y$ .

Donc il existe un entier relatif $k$ tel que $y=4k$ .

On remplace $y$ par $4k$ dans $4x=5y$ .

4x=5\times 4k\\x=5k

Les couples solutions de l’équation $4x=5y$ sont de la forme $(5k;4k)$ avec $k\in \mathbf{Z}$ .

Donc les couples solutions de l’équation $12x=15y$ sont de la forme $(5k;4k)$ avec $k\in \mathbf{Z}$ .

On s’assure que les solutions trouvées sont bien solutions de l’équation $12x=15y$ .

L’égalité $12\times 5k=15\times 4k$ est bien vérifiée.

Exercice n°1

Résoudre les équations suivantes où $x$ et $y$ sont des entiers relatifs.

23x=19y

5(x-1)=3y

65x=91y

Exercice n°2

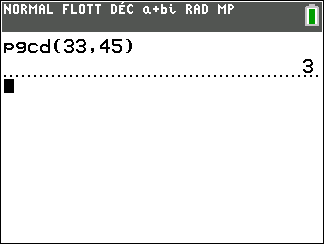
Déterminer les couples d’entiers relatifs tels que $33x-45y=0$

2. En déduire les couples d’entiers relatifs tels que $33x+45y=12$ .

Exercice n°3

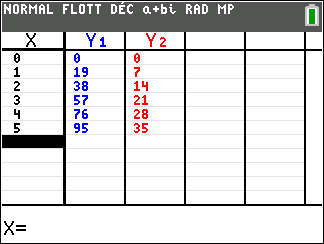
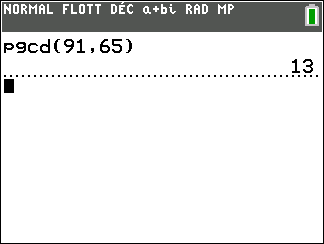
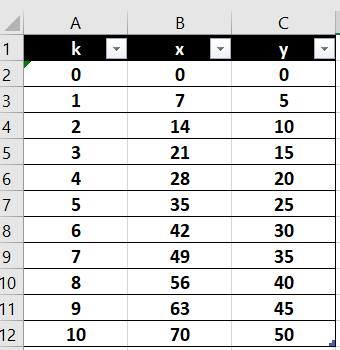
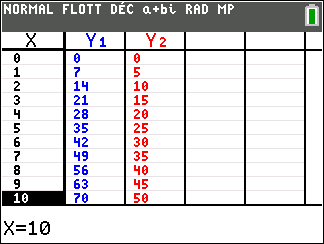
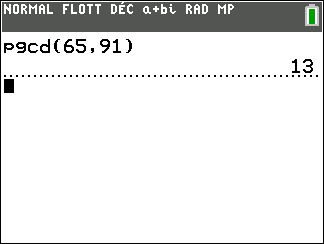
Déterminer les couples d’entiers naturels tels que

Exercice n°4

Déterminer le $PGCD(65;91)$ à l’aide de l’algorithme d’Euclide.

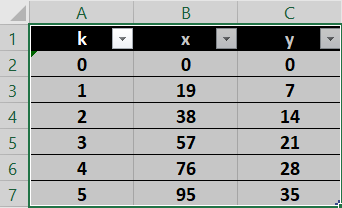
2. Déterminer les couples d’entiers naturels tels que

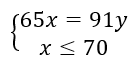
Corollaire

Soient $a$ , $b$ et $c$ trois entiers relatifs non nuls.

Si $a$ divise $c$ et si $b$ divise $c$ et si $a$ et $b$ sont premiers entre eux alors $ab$ divise $c$ .

Exercice n°5

Soit $n$ un entier naturel.

Justifier que, parmi les nombres $n,n+1,n+2$ l’un est divisible par $3$ et au moins un est divisible par $2$ .

2. En déduire que $n(n+1)(n+2)$ est divisible par $6$ .

Exercice n°6

Soit $n$ un entier naturel. Soit $A=n(n^4-1)$

Montrer que $A=n(n^4-1)$ est divisible par $2$

2. Montrer que $A=n(n^4-1)$ est divisible par $5$

3. En déduire que $A=n(n^4-1)$ est divisible par $10$

$n\equiv 0[5]$	$n\equiv 1[5]$	$n\equiv 2[5]$	$n\equiv 3[5]$	$n\equiv 4[5]$
$n^4\equiv 0[5]$	$n^4\equiv 1[5]$	$n^4\equiv 16[5]$	$n^4\equiv 81[5]$	$n^4\equiv 256[5]$
$n^4-1\equiv -1[5]$	$n^4-1\equiv 0[5]$	$n^4-1\equiv 15[5]$	$n^4-1\equiv 80[5]$	$n^4-1\equiv 255[5]$
$n(n^4-1)\equiv 0[5]$	$n(n^4-1)\equiv 0[5]$	$n(n^4-1)\equiv 30[5]\\n(n^4-1)\equiv 0[5]$	$n(n^4-1)\equiv 240[5]\\n(n^4-1)\equiv 0[5]$	$n(n^4-1)\equiv 1020[5]\\n(n^4-1)\equiv 0[5]$