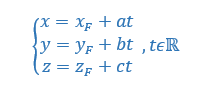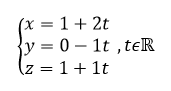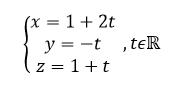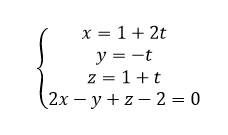logo

TS. Bac2021 espace exercice n°1

Exercice n°1 ( sujet 0 session 2021 )

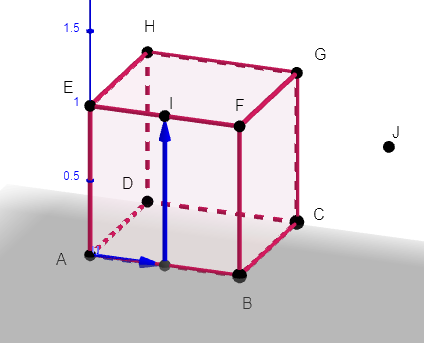
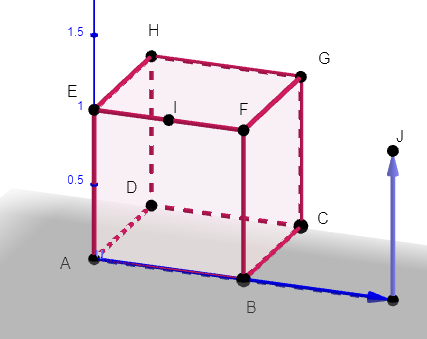
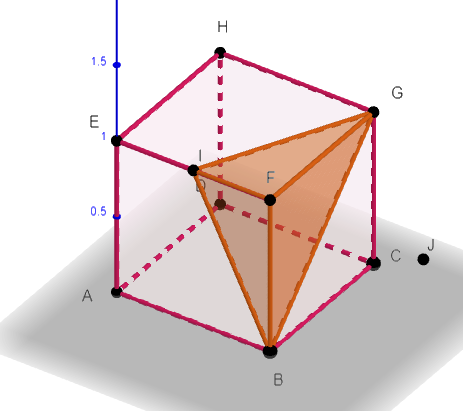
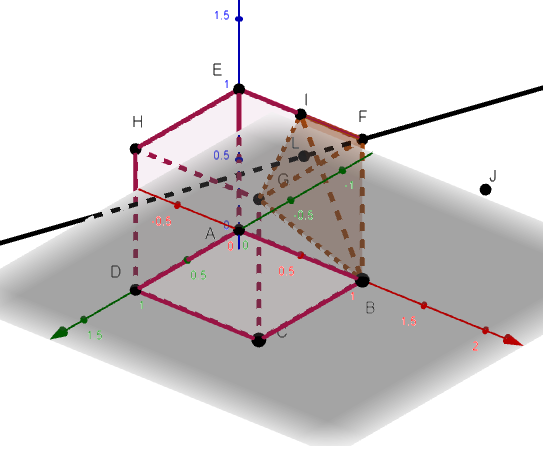
On considère le cube ABCDEFGH de côté 1, le milieu I de [EF] et et J le symétrique de E par rapport à F.

Dans tout l’exercice, l’espace est rapporté au repère orthonormé (A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}).

1. a. Par lecture graphique, donner les coordonnées des points I et J.

Pour afficher les coordonnées du point J, par exemple, cliquer droit sur le point J de la fenêtre active Géogébra ci-dessus. Apparaît alors Point  J(2;0;1).

correction point I
correction point J

b. En déduire les coordonnées des vecteurs \overrightarrow{DJ} , \overrightarrow{BI} et \overrightarrow{BG}.

Pour conjecturer les coordonnées du vecteur \overrightarrow{DJ}, par exemple, à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point D puis sur le point J. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées du vecteur \overrightarrow{DJ}.

correction \overrightarrow{DJ}
correction \overrightarrow{BI}
correction \overrightarrow{BG}

c. Montrer que \overrightarrow{DJ} est un vecteur normal au plan (BGI).

correction

d. Déterminer une équation cartésienne du plan (BGI).

Pour conjecturer une équation cartésienne du plan (BGI) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point B puis sur le point G et sur le point I . Dans la colonne Algèbre située à gauche, apparaît l’équation cartésienne du plan   (BGI) :x-0.5y+0.5z=1 .

correction

2. On note d la droite passant par F et orthogonale au plan (BGI).
a. Déterminer une représentation paramétrique de la droite d.

Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point F puis sur le plan (BGI) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(1,0,1)+\lambda (1,-0.5,0.5).

correction

b.  L est le point d’intersection de la droite d et du plan (BGI). Déterminer les coordonnées de L  par le calcul.

Pour conjecturer les coordonnées du point L à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le plan (BGI) . Dans la colonne Algèbre située à gauche, apparaît  K=intersection(f,p)   :  (0.67,0.17,0.83).

Remarque : on peut renommer K en L.

utiliser la TI 83 CE pour résoudre un système
correction

3. On rappelle que le volume V d’une pyramide est donné par la formule
V=\frac{1}{3}\times B\times h
où B  est l’aire d’une base et h la hauteur associée à cette base.

a. Calculer le volume de la pyramide FBGI.

Pour conjecturer le volume de la pyramide FBGI à l’aide de la fenêtre active géogébra ci-dessus. Saisir dans la colonne Algèbre  Pyramide(I,F,G,B), apparaît alors en dessous le nombre 0.08 qui est son volume.

correction

b. En déduire l’aire du triangle BGI.

Pour conjecturer l’aire du triangle BGI à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le cinquième onglet en haut à partir de la gauche et sélectionner Polygone dans le menu déroulant. Dans le repère cliquer sur le point B puis sur le point G et sur le point I . Dans la colonne Algèbre située à gauche, apparaît l’aire du triangle BGI  :  0.61 .

correction

©2020 – Math’O karé SAS

Pour déterminer les coordonnées du point I, il faut :

Partir de l’origine  A  pour se rendre au point I  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  \frac{1}{2}\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc I(\frac{1}{2};0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

Pour déterminer les coordonnées du point J, il faut :

Partir de l’origine  A  pour se rendre au point J  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

On part de  A, on se déplace de  2\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE}. 

Donc J(2;0;1) dans le repère  (A; \overrightarrow{AB};\overrightarrow{AD}; \overrightarrow{AE}).

On calcule les coordonnées du vecteur \overrightarrow{DJ}.

Je repère les coordonnées des points D et J.

\hspace{0.2cm}x_{D}\hspace{0.05cm}y_{D}\hspace{0.05cm}z_{D}\hspace{2.1cm}x_{J}\hspace{0.05cm}y_{J}\hspace{0.05cm}z_{J}

D(0;1;0)\hspace{2cm}J(2;0;1)

J’écris la formule :

\overrightarrow{DJ}(x_{J}-x_{D};y_{I}-y_{D};z_{I}-z_{D})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{DJ}(2-0;0-1;1-0)

\overrightarrow{DJ}(2;-1;1)

 

On calcule les coordonnées du vecteur \overrightarrow{BI}.

Je repère les coordonnées des points B et I.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{I}\hspace{0.05cm}y_{I}\hspace{0.05cm}z_{I}

B(1;0;0)\hspace{2cm}I(\frac{1}{2};0;1)

J’écris la formule :

\overrightarrow{BI}(x_{I}-x_{B};y_{I}-y_{B};z_{I}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BI}(\frac{1}{2}-1;0-0;1-0)

\overrightarrow{BI}(-\frac{1}{2};0;1)

On calcule les coordonnées du vecteur \overrightarrow{BG}.

Je repère les coordonnées des points B et G.

\hspace{0.2cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}\hspace{2.1cm}x_{G}\hspace{0.05cm}y_{G}\hspace{0.05cm}z_{G}

B(1;0;0)\hspace{2cm}G(1;1;1)

J’écris la formule :

\overrightarrow{BG}(x_{G}-x_{B};y_{G}-y_{B};z_{G}-z_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BG}(1-1;1-0;1-0)

\overrightarrow{BG}(0;1;1)

On remarque que \overrightarrow{BI}(-\frac{1}{2};0;1)et \overrightarrow{BG}(0;1;1) ne sont pas colinéaires car leurs coordonnées ne sont pas proportionnelles.

On calcule le produit scalaire  \overrightarrow{DJ}.\overrightarrow{BI}.

\overrightarrow{DJ}(2;-1;1).

\overrightarrow{BI}(-\frac{1}{2};0;1).

Pour calculer  \overrightarrow{DJ}.\overrightarrow{BI}, on remplace : 

 x par 2 ,  y par (-1) ,  z par 1.

 x’ par (-\frac{1}{2}) ,  y’ par 0 ,  z’ par 1, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{DJ}.\overrightarrow{BI}=2\times (-\frac{1}{2})+(-1)\times 0+1\times 1\\\overrightarrow{DJ}.\overrightarrow{BI}=-1+0+1\\\overrightarrow{DJ}.\overrightarrow{BI}=0

Donc les vecteurs  \overrightarrow{DJ} et  \overrightarrow{BI} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{DJ}.\overrightarrow{BG}.

\overrightarrow{DJ}(2;-1;1).

\overrightarrow{BG}(0;1;1).

Pour calculer  \overrightarrow{DJ}.\overrightarrow{BG}, on remplace : 

 x par 2 ,  y par (-1) ,  z par 1.

 x’ par 0 ,  y’ par 1 ,  z’ par 1, dans:

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{DJ}.\overrightarrow{BG}=2\times 0+(-1)\times 1+1\times 1\\\overrightarrow{DJ}.\overrightarrow{BG}=0-1+1\\\overrightarrow{DJ}.\overrightarrow{BG}=0

Donc les vecteurs  \overrightarrow{DJ} et  \overrightarrow{BG} sont orthogonaux.

Le vecteur   \overrightarrow{DJ} est orthogonal à   \overrightarrow{BI} et \overrightarrow{BG}, donc il est normal au plan (BGI)

On veut déterminer une équation cartésienne du plan  (BGI) de vecteur normal \overrightarrow{DJ}.

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{DJ} a pour coordonnées (2;-1;1).

On remplace a par 2 et b par -1 et c par 1 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (BGI) est de la forme :

2x-y+z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(BGI) passe par B(1;0;0), on remplace x par 1,  y par 0 et z par 0 dans 2x-y+z+d=0.

2\times 1-0+0+d=0

2+d=0

d=-2

Une équation cartésienne du plan  (BGI) est 2x-y+z-2=0

d est la droite passant par F et orthogonale au plan (BGI).
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (BGI), alors le vecteur normal au plan  \overrightarrow{n}(2;-1;1) est un vecteur directeur de la droite d.

De plus la droite d passe par le point F(1;0;1).

On remplace x_F par 1, y_F par 0, z_F par 1 ,a par 2, b par -1 et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

Remarque : la représentation donnée par géogébra est exacte aussi car les vecteurs de coordonnées (2;-1;1) et (1;-0.5;0.5) sont colinéaires.

 

L est le point d’intersection de la droite d et du plan (BGI). 

L\in d donc ses coordonnées vérifient le système 

L\in (BGI) donc ses coordonnées vérifient l’équation 2x-y+z-2=0 

Comme L est le point d’intersection de la droite d et du plan (BGI). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

2(1+2t)-(-t)+(1+t)-2=0\\2+4t+t+1+t-2=0\\6t+1=0\\6t=-1\\t=-\frac{1}{6}

Pour trouver les valeurs de x,y,z, on remplace t par -\frac{1}{6} dans les 3 premières équations.

x=1+2\times(-\frac{1}{6})\\x=1-\frac{1}{3}\\x=\frac{2}{3}
y=-(-\frac{1}{6})\\y=\frac{1}{6}

 

z=1+(-\frac{1}{6})\\x=1-\frac{1}{6}\\x=\frac{5}{6}

Donc L a pour coordonnées (\frac{2}{3};\frac{1}{6};\frac{5}{6}).

 

 

Pour déterminer le volume de la pyramide FBGI, il faut choisir une base. Ici on choisit le triangle rectangle isocèle FBG. La hauteur correspondante sera  [IF].

L’aire du triangle FBG est la moitié du carré FBCG de côté 1, elle vaut \frac{1}{2}.

IF=\frac{EF}{2}=\frac{1}{2}

Pour calculer le volume de la pyramide, on remplace B par \frac{1}{2} et h par \frac{1}{2} dans la formule B par V=\frac{B\times h}{3}

V=\frac{\frac{1}{2}\times \frac{1}{2}}{3}

V=\frac{\frac{1}{4}}{3}

V=\frac{1}{12}

 

 

Le volume de la pyramide FBGI ne change pas si on change la base. Ici on choisit le triangle  BGI. La hauteur correspondante sera  [FL].

V=\frac{aire(BGI)\times FL}{3}

\frac{aire(BGI)\times FL}{3}=\frac{1}{12}

On calcule la distance FL.

F(1;0;1)\\L(\frac{2}{3};\frac{1}{6};\frac{5}{6})

Pour calculer la distance FL de la pyramide, on remplace x_L par \frac{2}{3} , y_L par \frac{1}{6} , z_L par \frac{5}{6} , x_F par 1 , y_F par 0 et z_F par 1dans la formule

FL=\sqrt{(x_L-x_F)^2+(y_L-y_F)^2+(z_L-z_F)^2}

FL=\sqrt{(\frac{2}{3}-1)^2+(\frac{1}{6}-0)^2+(\frac{5}{6}-1)^2}

On effectue ce qu’il y a entre parenthèses 

FL=\sqrt{(\frac{2}{3}-\frac{3}{3})^2+(\frac{1}{6})^2+(\frac{5}{6}-\frac{6}{6})^2}\\FL=\sqrt{(-\frac{1}{3})^2+(\frac{1}{6})^2+(-\frac{1}{6})^2}

On effectue les puissances

FL=\sqrt{\frac{1}{9}+\frac{1}{36}+\frac{1}{36}}

On ajoute en mettant au même dénominateur

FL=\sqrt{\frac{1}{9}\times \frac{4}{4}+\frac{1}{36}+\frac{1}{36}}\\FL=\sqrt{\frac{4}{36}+\frac{1}{36}+\frac{1}{36}}\\FL=\sqrt{\frac{6}{36}}\\FL=\sqrt{\frac{1}{6}}

Pour déterminer l’aire de BGI , on remplace FL par \sqrt{\frac{1}{6}} dans  \frac{aire(BGI)\times FL}{3}=\frac{1}{12}

\frac{aire(BGI)\times \sqrt{\frac{1}{6}}}{3}=\frac{1}{12}\\aire(BGI)\times \sqrt{\frac{1}{6}}=3\times \frac{1}{12}\\aire(BGI)\times \sqrt{\frac{1}{6}}=\frac{1}{4}\\aire(BGI)=\frac{\frac{1}{4}}{\sqrt{\frac{1}{6}}}\\aire(BGI)=\frac{1}{4}\times{\sqrt{6}}\\aire(BGI)=\frac{\sqrt{6}}{4}

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.