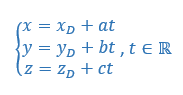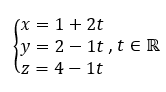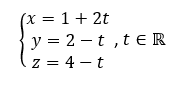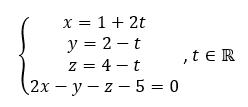Exercice n°1 Polynésie 5 mai 2022
L’espace est rapporté un repère orthonormal où l’on considère :
• les points A(2 ; −1 ; 0) , B(1 ; 0; -3) , C(6 ; 6 ; 1) et D(1 ; 2 ; 4).
• Le plan P d’équation cartésienne 2x-y-z+4=0
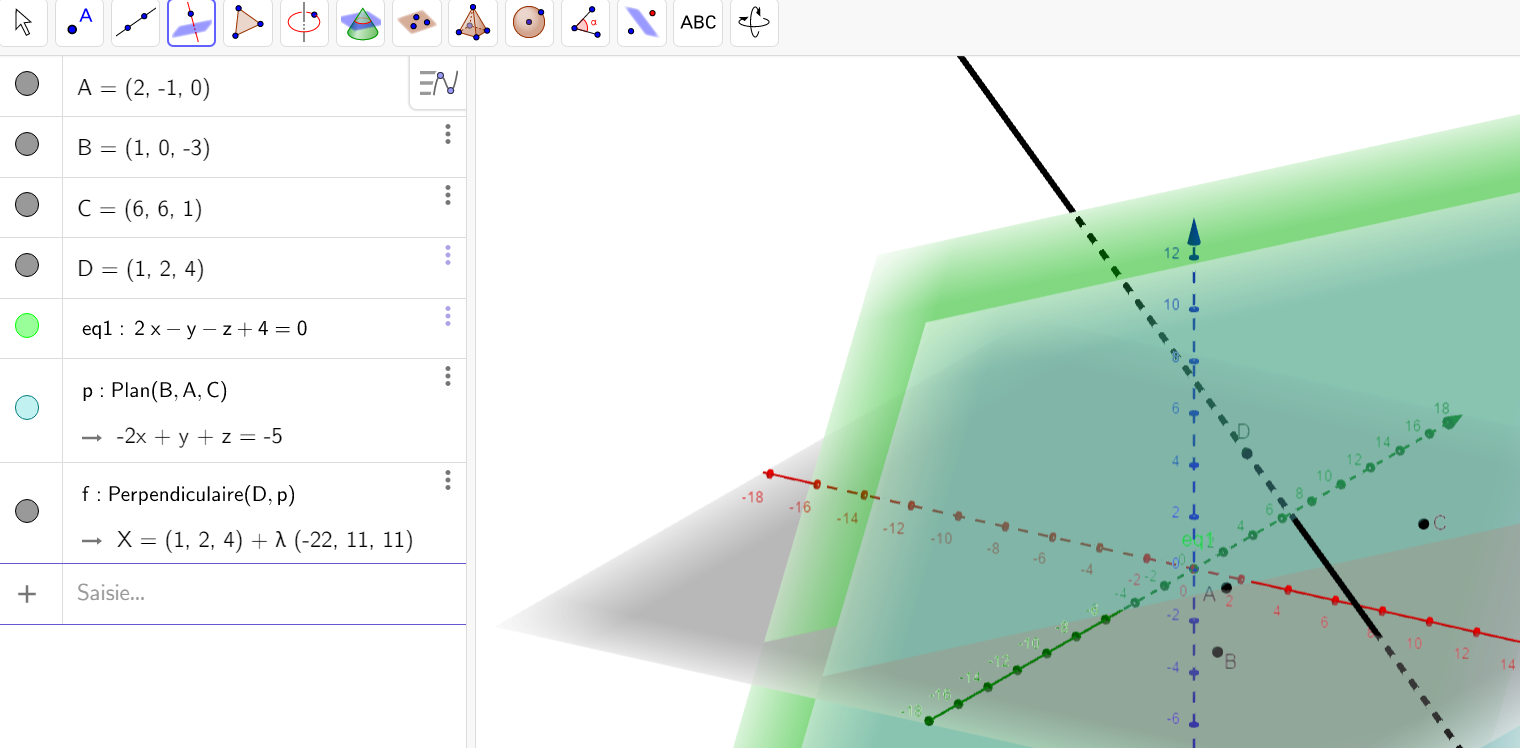
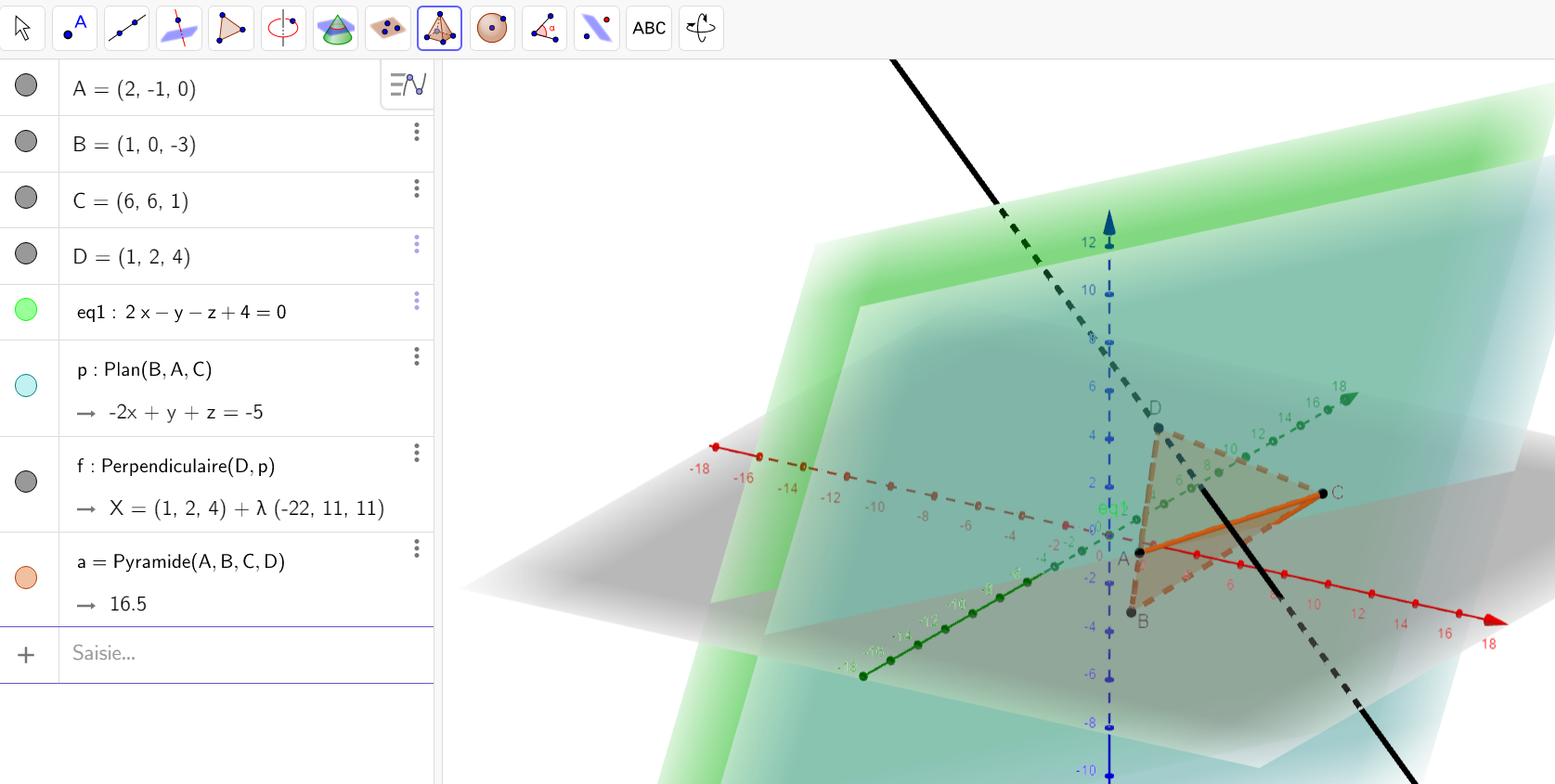
On va utiliser la fenêtre active Géogébra déjà complétée pour éventuellement conjecturer ou valider des réponses.
Pour placer A dans le repère, on a cliqué sur le deuxième onglet en haut à gauche puis on a saisi A=(2,-1,0) dans la colonne de gauche et on a validé avec enter.
Idem pour B,C,D.
Pour tracer le plan P dans le repère, cliquer sur le huitième onglet en haut à gauche puis saisir
2x-y-z+4=0 dans la colonne de gauche et valider avec enter.
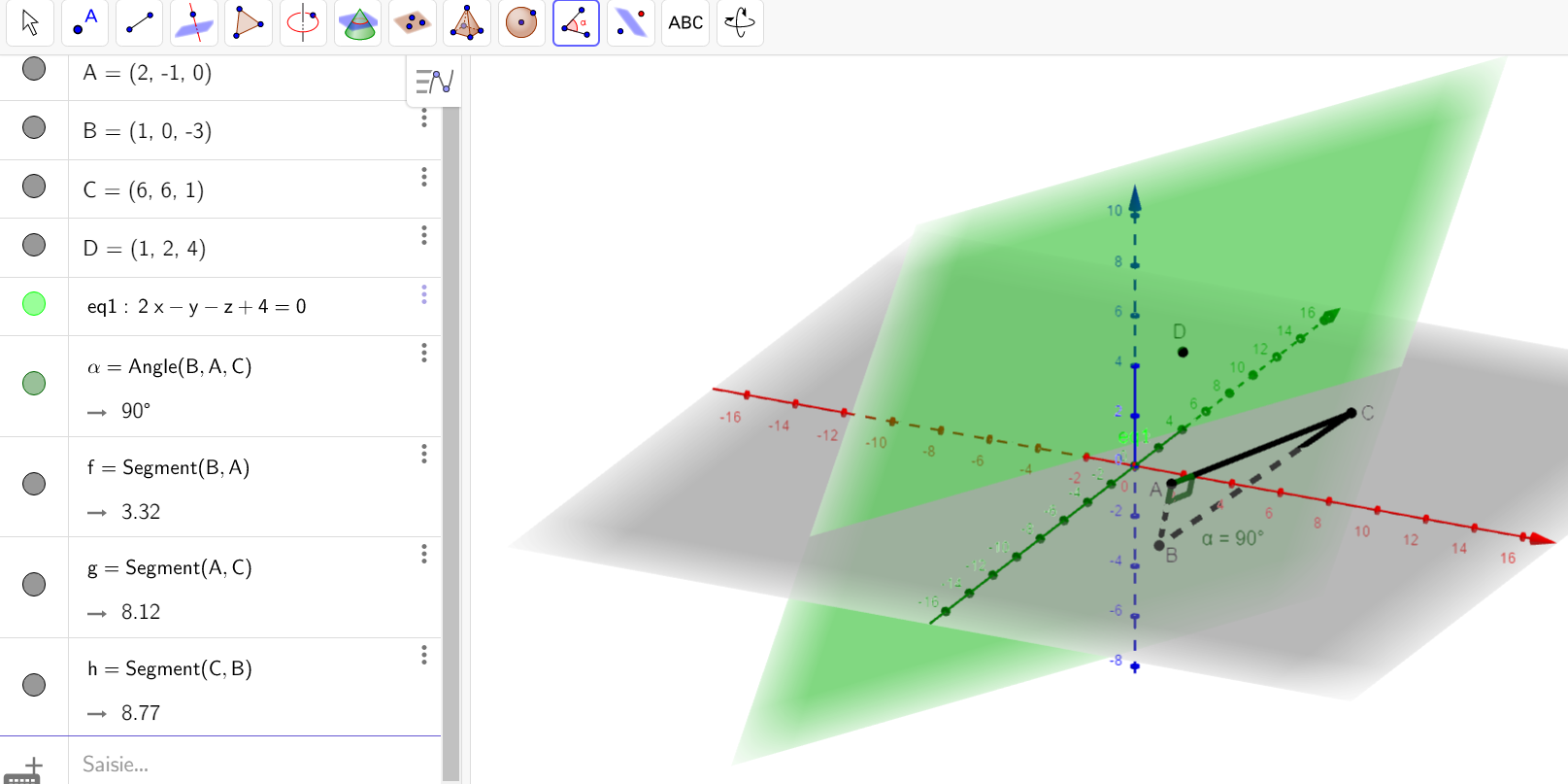
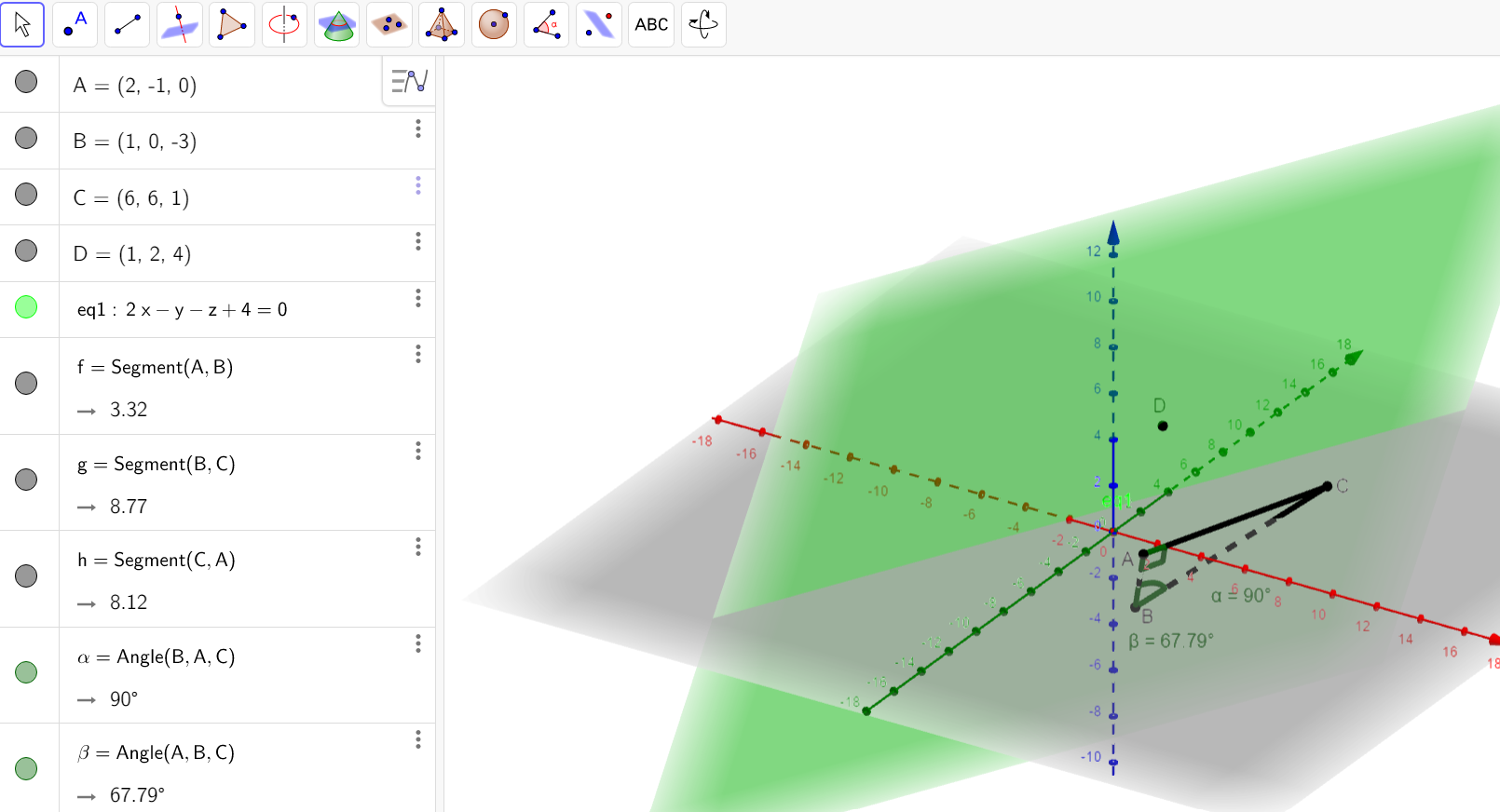
1. a. Démontrer que le triangle ABC est rectangle en A.
- b. Calculer le produit scalaire \overrightarrow{BA}.\overrightarrow{BC} puis les longueurs BA et BC.
- c. En déduire la mesure en degrés de l’angle \widehat{ABC} arrondie au degré.
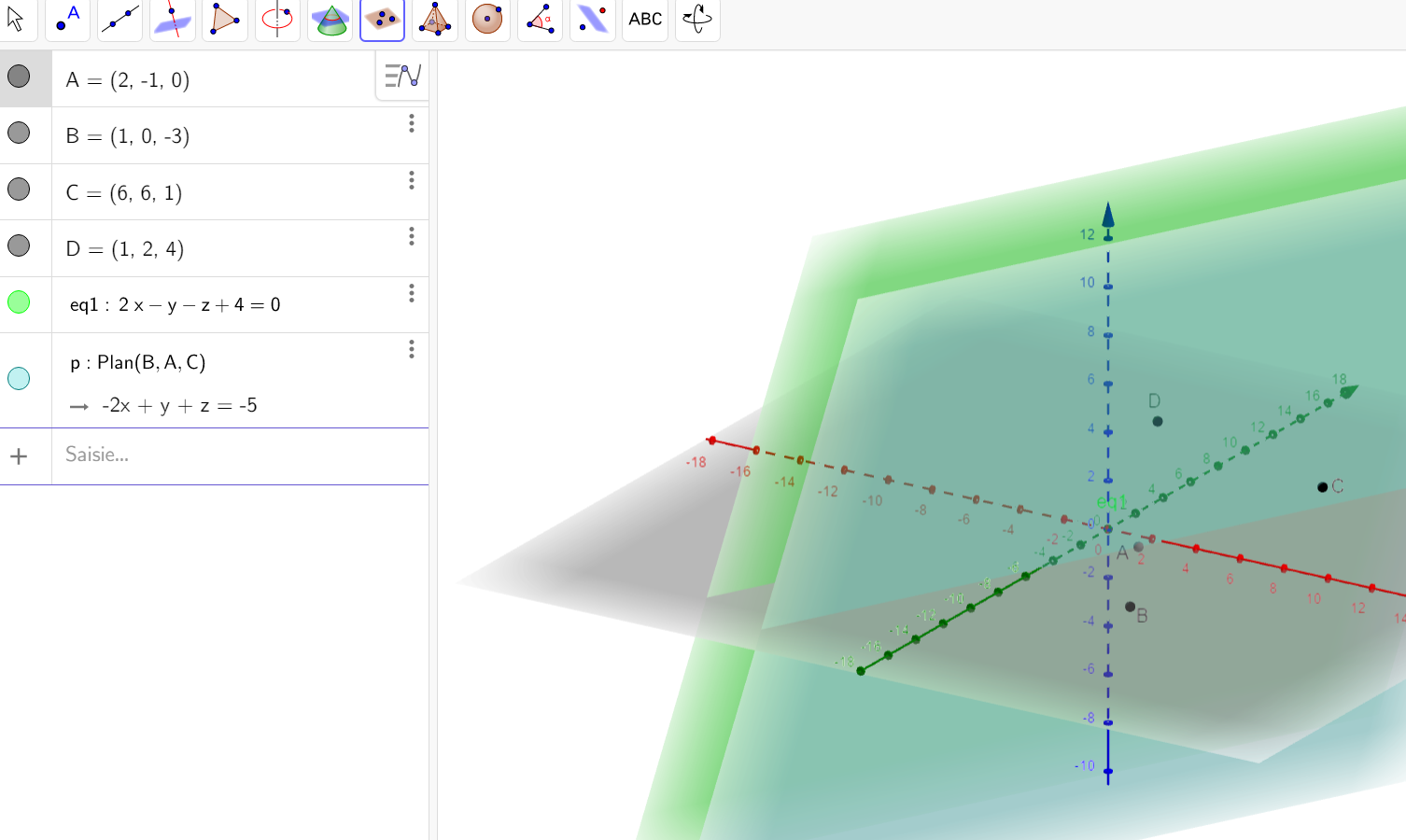
2. a. Démontrer que le plan P est parallèle au plan (ABC).
2. b. En déduire une équation cartésienne du plan (ABC).
2. c. Déterminer une représentation paramétrique de la droite d orthogonale au plan (ABC) et passant par le point D.
2. d. Démontrer que le projeté orthogonal H du point D sur le plan (ABC) a pour coordonnées (4;\frac{1}{2};\frac{5}{2})
3. On rappelle que le volume d’une pyramide est donné par V=\frac{1}{3}Bh où B désigne l’aire d’une base et h la hauteur de la pyramide associée à cette base.
Calculer l’aire du triangle ABC puis démontrer que le volume de la pyramide ABCD est égal à 16,5 unités de volume.