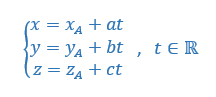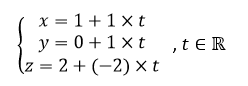logo

TS. Bac2021 espace exercice n°6

Exercice n°6 ( Métropole 13 Septembre 2021 J2 )

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n’est demandée.

Dans l’espace rapporté à un repère orthonormé (O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}), on considère le point A(1;0;2), le point B(2;1;0) et le point le point C(0;1;2). On considère la droite  d de représentation paramétrique 

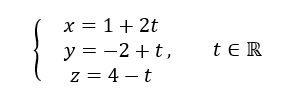
1. Parmi les points suivants, lequel appartient à la droite  d?

a. M(2;1;-1)

b. N(-3;-4;6)

c. P(-3;-4;2)

d. Q(-5;-5;1)

Pour placer le point M dans le repère à l’aide de la fenêtre active géogébra ci-dessus, saisir M=(2,1,-1) dans la colonne Algèbre située à gauche. Puis regarder si le point est sur la droite d.

correction

2. Le vecteur \overrightarrow{AB} admet pour coordonnées.

a. (1.5;0.5;1)

b. (-1;-1;2)

c. (1;1;-2)

d. (3;1;2)

Pour conjecturer les coordonnées de \overrightarrow{AB}à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B. Dans la colonne Algèbre située à gauche, apparaissent les coordonnées  (1,1,-2).

correction

3. Une représentation paramétrique de la droite  (AB) est:

Réponse a

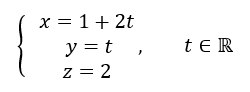
Réponse b

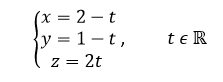
Réponse c

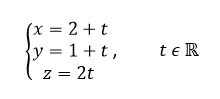
Réponse d

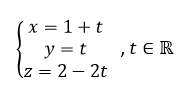
Pour conjecturer une représentation paramétrique de la droite (AB) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le troisième onglet en haut à partir de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer sur le point A puis sur le point B . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite (AB)  :  X=(2,1,0)+\lambda (-1,-1,2).

correction

4. Une équation cartésienne du plan passant par le point C et orthogonal à la droite d est :

a. x −2y +4z −6 = 0

b. 2x + y − z +1 = 0

c.  2x + y − z −1 = 0

d. y +2z −5 = 0

Pour conjecturer une équation cartésienne du plan passant par C et orthogonal à la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan perpendiculaire dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le point C . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   2x+y-z=-1.

correction

©2020 – Math’O karé SAS

On cherche quel point se trouve sur la droite d de représentation paramétrique :

a. M(2;1;-1)

b. N(-3;-4;6)

c. P(-3;-4;2)

d. Q(-5;-5;1)

Regardons si M est sur d. On peut, par exemple, déterminer pour quelle valeur de t, y=1.

y=1 si -2+t=1\\\hspace{2.1cm}t=1+2\\\hspace{2.1cm}t=3

On remplace ensuite t par le résultat trouvé  3 dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par 2 et t par 3 dans x=1+2t et on regarde si l’égalité est vérifiée.

2\ne 1+2\times3 donc M(2;1;-1) n’est pas sur d

Regardons si N est sur d. On peut, par exemple, déterminer pour quelle valeur de t, y=-4.

y=-4 si -2+t=-4\\\hspace{2.1cm}t=-4+2\\\hspace{2.1cm}t=-2

On remplace ensuite t par le résultat trouvé  (-2) dans les deux équations restantes et on regarde si les égalités sont vérifiées.

On remplace x par -3 et t par -2 dans x=1+2t et on regarde si l’égalité est vérifiée.

-3= 1+2\times(-2).

On remplace z par 6 et t par -2 dans z=4-t et on regarde si l’égalité est vérifiée.

6= 4-(-2).

donc N(-3;-4;6) est sur d.

La bonne réponse est la réponse b.

a. (1.5;0.5;1)

b. (-1;-1;2)

c. (1;1;-2)

d. (3;1;2)

On calcule les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.2cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(1;0;2)\hspace{2cm}B(2;1;0)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(2-1;1-0;0-2)

\overrightarrow{AB}(1;1;-2)

La bonne réponse est la réponse c.

On cherche une représentation paramétrique de la droite (AB) :

Réponse a

Réponse b

Réponse c

Réponse d

(AB) est la droite passant par A(1;0;2) et de vecteur directeur \overrightarrow{AB}(1;1;-2).  
On remplace x_A par 1, y_A par 0, z_A par 2 ,a par 1, b par 1 et c par -2 dans la représentation paramétrique :

La bonne réponse est la réponse d.

 

 

 

On cherche une équation cartésienne du plan passant par le point C et orthogonal à la droite d

La droite

a pour vecteur directeur \overrightarrow{n}(2;1;-1).

Ce vecteur est normal au plan. 

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

On remplace a par 2 et b par 1 et c par (-1) dans l’équation  ax+by+cz+d=0.

Une équation cartésienne du plan est de la forme :

2\times x+1\times y+(-1)\times z+d=0

2x+y-z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

Le plan passe par C(0;1;2), on remplace x par 0,  y par 1 et z par 2 dans 2x+y-z+d=0.

2\times 0+1\times 1-2+d=0

-1+d=0

d=1

Une équation cartésienne du plan  passant par le point C et orthogonal à la droite d est 2x+y-z+1=0.

La bonne réponse est la réponse B .

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.