logo

TE. Complexes : exercice n°1

Extrait du sujet du 16 juin 2015 donné en Asie au Bac S

Le plan est muni du repère orthonormé direct (O,\overrightarrow{u},\overrightarrow{v})
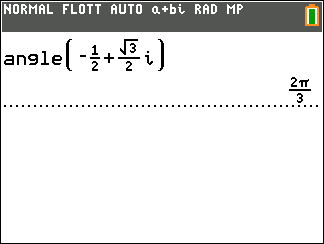
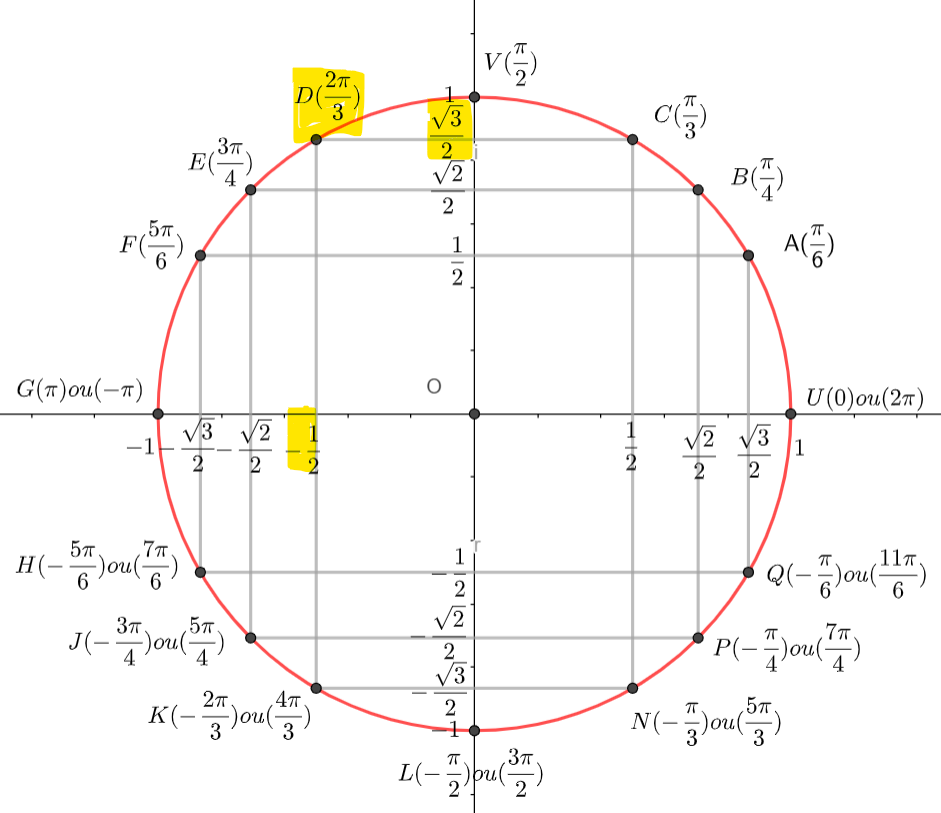
On donne le nombre complexe j=-\frac{1}{2}+i\frac{\sqrt{3}}{2}
Le but de cet exercice est d’étudier quelques propriétés du nombre j.
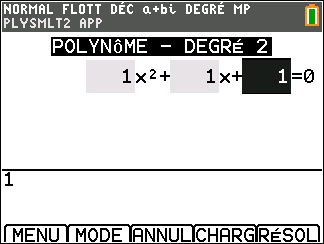
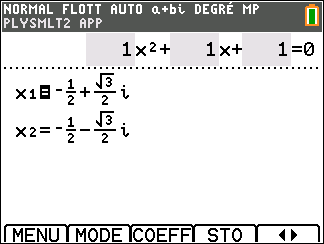
1. a. Résoudre dans l’ensemble \mathbf{C} des nombres complexes l’équation z^2+ z +1 = 0.

conjecture avec la TI 83
correction

b. Vérifier que le nombre complexe j est une solution de cette équation

correction

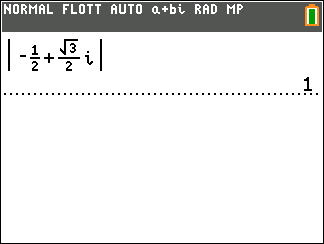
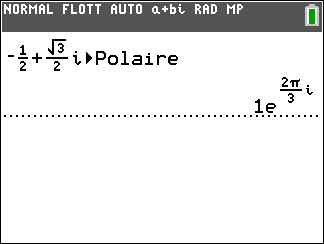
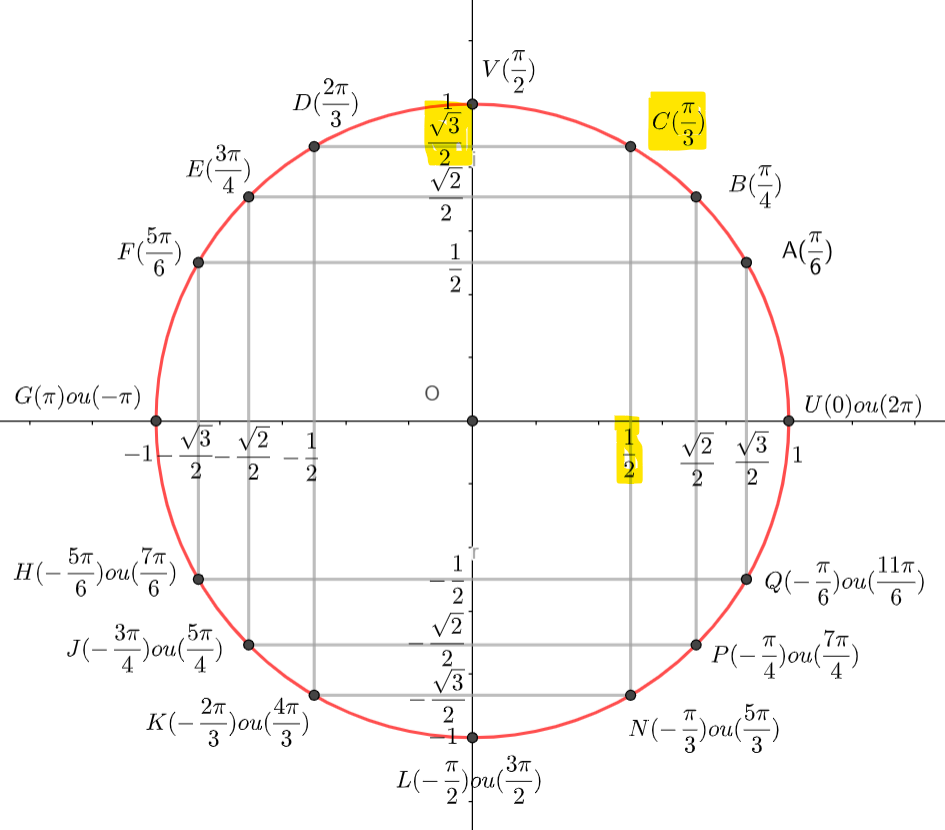
2. Déterminer le module et un argument du nombre complexe j, puis donner sa forme exponentielle.

conjecture avec la TI 83 : module
conjecture avec la TI 83 : argument
correction
valider la forme exponentielle avec la TI 83

3. Démontrer les égalités suivantes :

a. j^3=1

correction

b. j^2=-1-j

correction

4. On note P,Q,R les images respectives des nombres complexes 1,j,j^2 dans le plan.
a. Calculer \frac{j^2-1}{j-1} et mettre le résultat sous forme exponentielle.

correction

b. En déduire la nature du triangle PQR.

correction

©2020 – Math’O karé SAS

Utiliser la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  z^2+z+1=0.

C’est une équation du second degré d’inconnue z.

J’identifie les coefficients l’équation a=1, b=1 et c=1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,1,1.

\Delta=1²-4\times{1}\times{1}\\\Delta=1-4\\\Delta=-3

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,1,(-3).

z_1=\frac{-1-i\sqrt{-(-3)}}{2\times 1}\\z_1=\frac{-1-i\sqrt{3}}{2}\\z_1=-\frac{1}{2}-\frac{\sqrt{3}}{2}i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i

Je conclus S=\{-\frac{1}{2}-\frac{\sqrt{3}}{2}i;-\frac{1}{2}+\frac{\sqrt{3}}{2}i\}

 

On a montré précédemment que l’équation  z^2+z+1=0 a pour ensemble solution

S=\{-\frac{1}{2}-\frac{\sqrt{3}}{2}i;-\frac{1}{2}+\frac{\sqrt{3}}{2}i\}.

Comme j=-\frac{1}{2}+\frac{\sqrt{3}}{2}i, j\in S donc j est solution de l’équation z^2+z+1=0.

Déterminer le module d’un complexe avec la TI 83 premium CE.

Au clavier

A l’écran

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

Sur la 5ème ligne sélectionner abs( , puis saisir à la suite le nombre complexe.

 

Déterminer l’argument d’un complexe avec la TI 83 premium CE.

Au clavier

A l’écran

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

Sur la 4ème ligne sélectionner angle( , puis saisir à la suite le nombre complexe.

1.Calculons le module du nombre complexe  j=-\frac{1}{2}+\frac{\sqrt{3}}{2}i

On remplace a par la partie rélle de j qui vaut -\frac{1}{2} et b par la partie imaginaire de j qui vaut \frac{\sqrt{3}}{2} dans 

|z|=\sqrt{a^2+b^2}.

|j|=\sqrt{(-\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}\\\hspace{0.5cm}=\sqrt{\frac{1^2}{2^2}+\frac{\sqrt{3}^2}{2^2}}\\\hspace{0.5cm}=\sqrt{\frac{1}{4}+\frac{3}{4}}\\\hspace{0.5cm}=\sqrt{\frac{4}{4}}\\\hspace{0.5cm}=\sqrt{1}\\\hspace{0.5cm}=1

2. Calculons un argument du nombre complexe  j=-\frac{1}{2}+\frac{\sqrt{3}}{2}i c’est-à-dire qu’on cherche un réel \Theta tel que 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}

On remplace a par la partie rélle de j qui vaut -\frac{1}{2} et b par la partie imaginaire de j qui vaut \frac{\sqrt{3}}{2} et |j| par 1 dans 

cos(\Theta)=\frac{a}{|z|} et sin(\Theta)=\frac{b}{|z|}.

cos(\Theta)=\frac{-\frac{1}{2}}{1} et sin(\Theta)=\frac{\frac{\sqrt{3}}{2}}{1}

cos(\Theta)=-\frac{1}{2} et sin(\Theta)=\frac{\sqrt{3}}{2}

Pour déterminer, par le calcul, une valeur de \Theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\Theta)=-\frac{1}{2}

\Theta=cos^{-1}(-\frac{1}{2})

La  calculatrice donne \Theta=\frac{2\pi}{3}

En réalité on obtient :

\Theta=\frac{2\pi}{3} ou \Theta=-\frac{2\pi}{3}

sin(\Theta)=\frac{\sqrt{3}}{2}

\Theta=sin^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \Theta=\frac{\pi}{3}

En réalité on obtient :

\Theta=\frac{\pi}{3} ou \Theta=\pi-(\frac{\pi}{3})

\Theta=\frac{\pi}{3} ou \Theta=\frac{2\pi}{3}

La solution commune aux deux équations est : \Theta=\frac{2\pi}{3}.

Donc arg(z)=\frac{2\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place -\frac{1}{2} sur l’axe des abscisses, \frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{2\pi}{3}. attention il y a une infinité de mesures : \frac{2\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(j)=\frac{2\pi}{3}[2\pi].

3. On en déduit la forme exponentielle

j=1\times e^{i\frac{2\pi}{3}}\\j=e^{i\frac{2\pi}{3}}

 

 

Déterminer la forme exponentielle d’un complexe avec la TI 83 premium CE.

Au clavier

A l’écran

Saisir le nombre complexe

Appuyer sur la touche math du clavier de la calculatrice.

Se déplacer dans la colonne CMPLX.

Sur la 7ème ligne sélectionner Polaire , puis valider avec entrer

On veut démontrer l’égalité suivante : j^3=1.

Doit-on remplacer j par la forme algébrique -\frac{1}{2}+\frac{\sqrt{3}}{2}i ou par la forme exponentielle e^{i\frac{2\pi}{3}} ?

Réponse : pour calculer des additions et des soustractions, on utilise la forme algébrique. Pour calculer un produit, un quotient ou une puissance, on utilise la forme exponentielle. Donc comme on calcule j^3 et que c’est une puissance, on j par e^{i\frac{2\pi}{3}}.

j^3=(e^{i\frac{2\pi}{3}})^3\\\hspace{0.5cm}=e^{i\frac{2\pi}{3}\times 3}\\\hspace{0.5cm}=e^{i2\pi}\\\hspace{0.5cm}=1

 

 

On veut démontrer l’égalité suivante : j^2=-1-j.

On sait que j est solution de l’équation z^2+z+1=0 donc

j^2+j+1=0

On enlève j+1 de chaque côté de l’égalité

j^2=-j-1 ou j^2=-1-j.

On veut calculer \frac{j^2-1}{j-1} et mettre le résultat sous forme exponentielle.

On a intérêt à remplacer j^2-1 par (j-1)(j+1) puis simplifier.

\frac{j^2-1}{j-1}=\frac{(j-1)(j+1)}{j-1}\\\hspace{0.75cm}=j+1

Comment on va faire une addition : j+1, on remplace j par sa forme algébrique -\frac{1}{2}+\frac{\sqrt{3}}{2}i .

\hspace{0.75cm}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i +1\\\hspace{0.75cm}=\frac{1}{2}+\frac{\sqrt{3}}{2}i

1.Calculons le module du nombre complexe  \frac{1}{2}+\frac{\sqrt{3}}{2}i

On remplace a par la partie rélle  qui vaut \frac{1}{2} et b par la partie imaginaire qui vaut \frac{\sqrt{3}}{2} dans 

|z|=\sqrt{a^2+b^2}.

|\frac{1}{2}+\frac{\sqrt{3}}{2}i|=\sqrt{(\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}\\\hspace{1.5cm}=\sqrt{\frac{1^2}{2^2}+\frac{\sqrt{3}^2}{2^2}}\\\hspace{1.5cm}=\sqrt{\frac{1}{4}+\frac{3}{4}}\\\hspace{1.5cm}=\sqrt{\frac{4}{4}}\\\hspace{1.5cm}=\sqrt{1}\\\hspace{1.5cm}=1

2. On cherche un réel \theta tel que 

cos(\theta)=\frac{a}{|z|} et sin(\theta)=\frac{b}{|z|}

On remplace a par la partie rélle qui vaut \frac{1}{2} et b par la partie imaginaire qui vaut \frac{\sqrt{3}}{2} et |\frac{1}{2}+\frac{\sqrt{3}}{2}i| par 1 dans 

cos(\theta)=\frac{a}{|z|} et sin(\theta)=\frac{b}{|z|}.

cos(\theta)=\frac{1}{2} et sin(\theta)=\frac{\sqrt{3}}{2}

Pour déterminer, par le calcul, une valeur de \theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\theta)=\frac{1}{2}

\theta=cos^{-1}(\frac{1}{2})

La  calculatrice donne \theta=\frac{\pi}{3}

En réalité on obtient :

\theta=\frac{\pi}{3} ou \theta=-\frac{\pi}{3}

sin(\theta)=\frac{\sqrt{3}}{2}

\theta=sin^{-1}(\frac{\sqrt{3}}{2})

La  calculatrice donne \theta=\frac{\pi}{3}

En réalité on obtient :

\theta=\frac{\pi}{3} ou \theta=\pi-\frac{\pi}{3}

La solution commune aux deux équations est : \theta=\frac{\pi}{3}.

Donc arg(\frac{1}{2}+\frac{\sqrt{3}}{2}i)=\frac{\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{1}{2} sur l’axe des abscisses, \frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{\pi}{3}. attention il y a une infinité de mesures : \frac{\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(\frac{1}{2}+\frac{\sqrt{3}}{2}i)=\frac{\pi}{3}[2\pi].

3. Mise sous forme exponentielle

La forme exponentielle de \frac{1}{2}+\frac{\sqrt{3}}{2}i est 1\times e^{\frac{\pi}{3}} ou e^{\frac{\pi}{3}}

 

 

 

On a montré que 

\frac{j^2-1}{j-1}=e^{i\frac{\pi}{3}}

Donc \frac{z_R-z_P}{z_Q-z_P}=e^{i\frac{\pi}{3}}

Ces deux complexes sont égaux donc

Leurs modules sont égaux

|\frac{z_R-z_P}{z_Q-z_P}|=|e^{i\frac{\pi}{3}}|

\frac{|z_R-z_P|}{|z_Q-z_P|}=1

On interprète le module de la différence de deux complexes comme une distance.

\frac{PR}{PQ}=1

PR=PQ

Leurs arguments sont égaux

arg(\frac{z_R-z_P}{z_Q-z_P})=arg(e^{i\frac{\pi}{3}})

arg(\frac{z_R-z_P}{z_Q-z_P})=\frac{\pi}{3}

On interprète l’argument du rapport de différences de complexes comme un angle.

(\overrightarrow{PQ},\overrightarrow{PR})=\frac{\pi}{3}

Donc le triangle PQR est équilatéral.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.