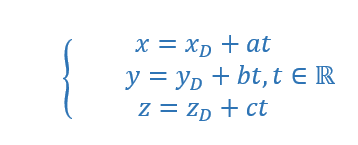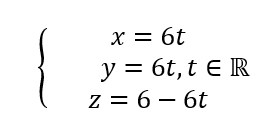Dans l’espace muni d’un repère orthonormé (O,\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}), on considère les points A(0;8;6), B(6;4;4) et C(2;4;0).
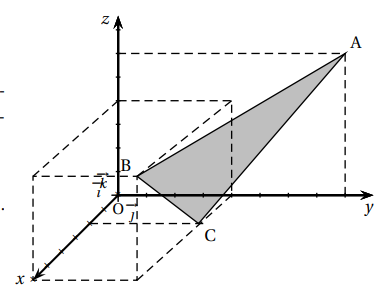
On pourra utiliser la page Géogébra active ci-dessous pour conjecturer les résultats aux questions posées.
1. a. Justifier que les points A, B et C ne sont pas alignés.
On conjecture avec Géogébra :
On peut montrer que les coordonnées des vecteurs \overrightarrow{AB} et \overrightarrow{AC} ne sont pas proportionnelles.
Construction du vecteur \overrightarrow{AB} :
On clique sur le troisième onglet en partant de la gauche, on sélectionne vecteur dans le menu déroulant. Dans le repère on clique sur A puis sur B et dans la colonne de gauche on lit les coordonnées de (6,-4,-2).
Construction du vecteur \overrightarrow{AC} : on obtient de la même façon \overrightarrow{AC}(2;-4;-6).
Et on constate que les coordonnées ne sont pas proportionnelles.
b. Montrer que le vecteur \overrightarrow{n}(1;2;-1) est un vecteur normal au plan (ABC).
On conjecture avec Géogébra :
On peut montrer que le vecteur \overrightarrow{n}(1;2;-1) est orthogonal à \overrightarrow{AB} et à \overrightarrow{AC}
Construction du vecteur \overrightarrow{n} :
On clique sur le troisième onglet en partant de la gauche, on sélectionne vecteur dans le menu déroulant. Dans la colonne de gauche on saisit n=(1,2,-1).
Mesure de l’angle entre \overrightarrow{n} et \overrightarrow{AB} :
On construit un représentant de \overrightarrow{n} à partir du point A.
On clique sur le troisième onglet en partant de la gauche, on sélectionne Représentant dans le menu déroulant. Dans le repère on clique sur A puis sur n.
Ce représentant se nomme \overrightarrow{AA’}
On mesure l’angle \widehat{BAA’}
On clique sur le onzième onglet en partant de la gauche, on sélectionne Angle dans le menu déroulant. Dans le repère on clique sur A’ puis A puis B et on obtient 90°.
On procède de la même façon pour montrer que le vecteur \overrightarrow{n} est orthogonal à \overrightarrow{AC}
c. Déterminer une équation cartésienne du plan (ABC).
On conjecture avec Géogébra :
Construction du plan (ABC) :
On clique sur le huitième onglet en partant de la gauche, on sélectionne Plan passant par trois points dans le menu déroulant. Dans le repère, on clique sur A, B et C. Dans la colonne de gauche, apparaît une équation cartésienne du plan ABC : x+2y-z=10.
2. Soient D et E les points de coordonnées respectives (0;0;6) et (6;6;0).
a. Déterminer une représentation paramétrique de la droite (DE).
On conjecture avec Géogébra :
On place D et E .
On clique sur le deuxième onglet en partant de la gauche, on sélectionne Point dans le menu déroulant. Dans la colonne de gauche on saisit D=(0,0,6) puis E=(6,6,0).
Construction de la droite (DE) :
On clique sur le troisième onglet en partant de la gauche, on sélectionne Droite dans le menu déroulant. Dans le repère, on clique sur D et E. Dans la colonne de gauche, apparaît une représentation paramétrique de (DE) : X=(0,0,6)+\lambda (6,6,-6).
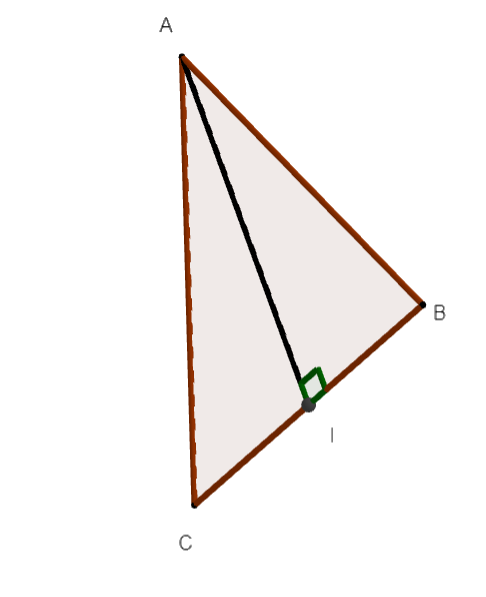
b. Montrer que le milieu I du segment [BC] appartient à la droite (DE).
3. On considère le triangle ABC.
a. Déterminer la nature du triangle ABC.
On conjecture avec Géogébra :
Construction du triangle ABC :
On clique sur le cinquième onglet en partant de la gauche, on sélectionne Polygone dans le menu déroulant. Dans le repère, on clique sur A,B,C et A. Dans la colonne de gauche, apparaissent les distances des trois côtés. On constate que le triangle ne peut pas être rectangle mais qu’il est isocèle en A.
b. Calculer l’aire du triangle ABC en unité d’aire.
On conjecture avec Géogébra :
Calcul de l’aire du triangle ABC :
On clique sur le onzième onglet en partant de la gauche, on sélectionne Aire dans le menu déroulant. Dans le repère, on clique sur le triangle ABC. Dans la colonne de gauche, apparaît l’aire de ABC; elle vaut 19.6.
c. Calculer \overrightarrow{AB}.\overrightarrow{AC}.
d. En déduire une mesure de l’angle \widehat{BAC} arrondie à 0,1 degré.
4. On considère le point H de coordonnées (\frac{5}{3},\frac{10}{3} , -\frac{5}{3}).
Montrer que H est le projeté orthogonal du point O sur le plan (ABC).
En déduire la distance du point O au plan (ABC).