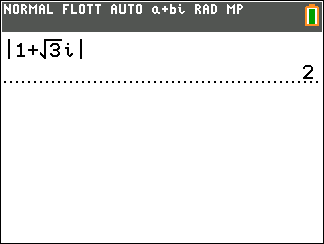
1. On considère l’équation (E) z^3=4z^2-8z+8
ayant pour inconnue le nombre complexe z.
a. Démontrer que, pour tout nombre complexe z,
z^3-4z^2+8z-8=(z-2)(z^2-2z+4)
b. Résoudre l’équation (E).
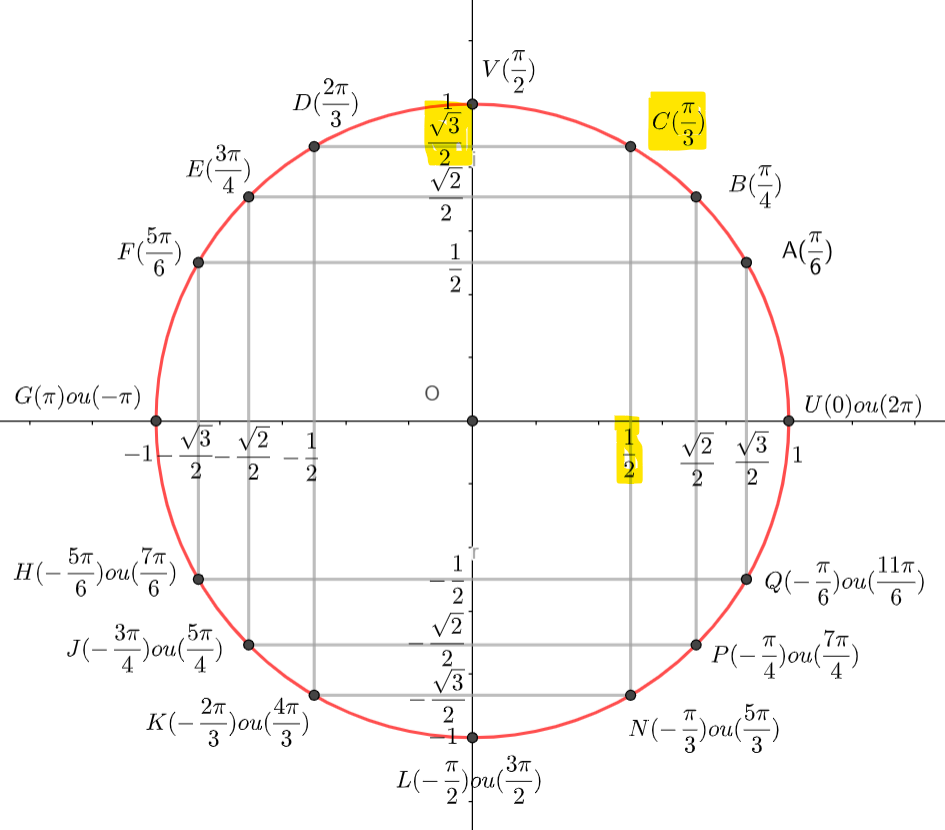
c. Écrire les solutions de l’équation (E) sous forme exponentielle.
On munit le plan complexe d’un repère orthonormé direct (O,\overrightarrow{u},\overrightarrow{v}).
Soit A,B,C et D les quatre points d’affixes respectives
z_A=1+i\sqrt{3} , z_B=2 , z_C=1-i\sqrt{3} et z_D=1.
Remarque : parmi les affixes ci-dessus, se trouvent les trois solutions trouvées à la question précédente . On peut donc valider la réponse de la question 1.c.
Ces quatre points sont représentés dans la figure ci-dessous.
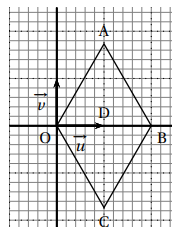
On peut utiliser la fenêtre active Géogébra si nécessaire.
2. Quelle est la nature du quadrilatère OABC ? Justifier.
3. Soit M le point d’affixez_M=\frac{7}{4}+i\frac{\sqrt{3}}{4}.
a. Démontrer que les points A,M et B sont alignés
b. Démontrer que le triangle DMB est rectangle.