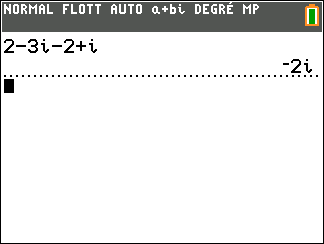
Exercice n°1
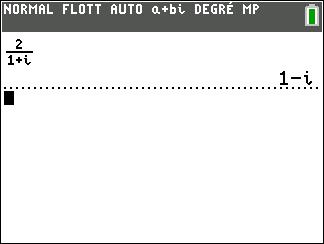
Déterminer dans chaque cas, les parties réelle et imaginaire des complexes suivants.
z=3+2i
z=-1+i
z=-2i+6
z=9
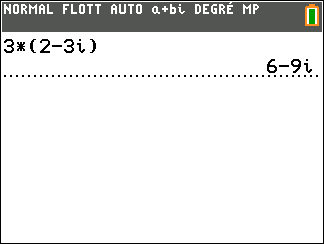
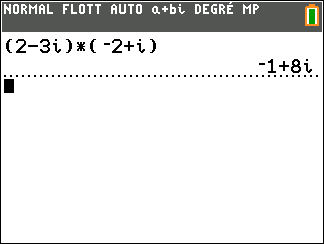
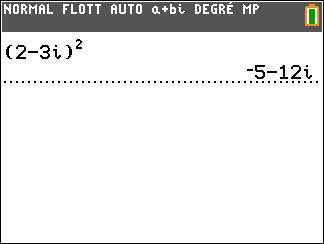
Exercice n°2 :
On considère z_1=2-3i et z_2=-2+i
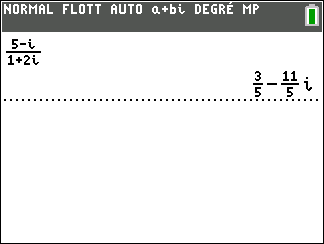
Déterminer la forme algébrique des complexes suivants.
z_1+z_2
z=3z_1
z_1\times z_2
z_1^2
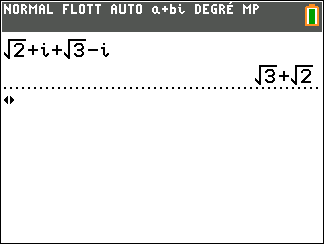
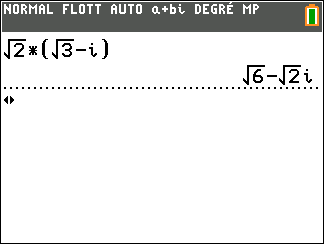
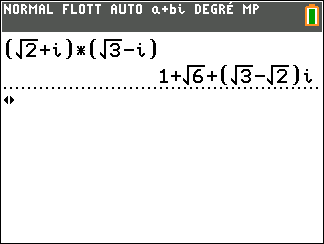
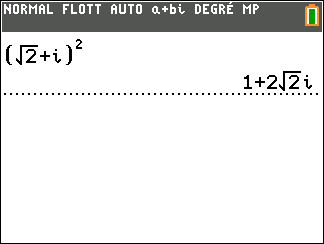
Exercice n°3
On considère z_1=\sqrt{2}+i et z_2=\sqrt{3}-i
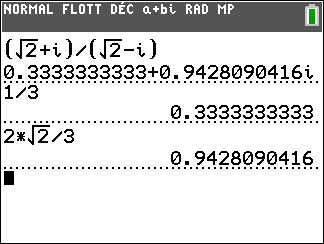
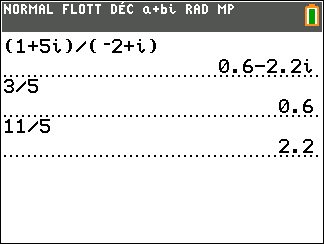
Déterminer la forme algébrique des complexes suivants.
z_1+z_2
z=\sqrt{2}z_2
z_1\times z_2
z_1^2
Exercice n°4 : Résoudre les équations suivantes dans \mathbf{C}.
On pourra conjecturer la ou les solutions à l’aide de la fenêtre active Géogébra ci-dessous. Quand on clique sur la première ligne pour saisir l’équation, le pavé numérique apparaît. Pour obtenir le i, il faut cliquer sur l’onglet f(x).
1+3i+z=2+5i
3+2z=3-4i
5i-3z=3-i
6+2i+2z=8+4i
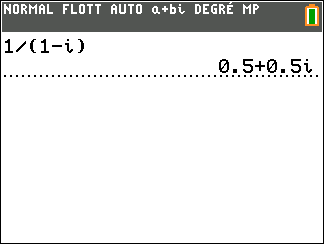
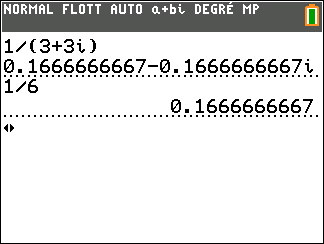
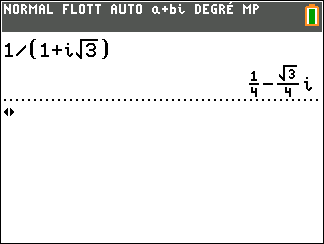
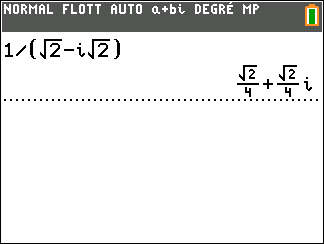
Exercice n°5
Déterminer la forme algébrique de l’inverse des nombres complexes suivants.
z=1-i
z=3+3i
1+i\sqrt{3}
\sqrt{2}-i\sqrt{2}
Exercice n°6 : Déterminer dans chaque cas, la partie réelle et la partie imaginaire des nombres complexes suivants.
z_1=\frac{2}{1+i}
z_2=\frac{5-i}{1+2i}
z_3=\frac{\sqrt{3}+2i}{\sqrt{3}+i}
z_4=\frac{1+5i}{-2+i}
Exercice n°7 : Résoudre les équations suivantes dans \mathbf{C}.
On pourra conjecturer la ou les solutions à l’aide de la fenêtre active Géogébra ci-dessus.
(1-i)z=1+i
iz=3+2i
(2+i)z=2-2i
2iz=3-4i