1) Résoudre graphiquement un système de deux équations a deux
inconnues.
Exemple n°1 : Résoudre graphiquement le système de deux
équations a deux inconnues suivant :
y=-x+4\\y=2x-2
On trace les deux droites dans le repère avec la méthode de son choix.
Dans y=-x+4 on identifie a=2 et b=-2. On place 4 sur l’axe des ordonnées. A partir du point de coordonnées (0;4) , j’avance horizontalement de 1 vers la droite et je descends de 1 (a=-1). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.
[…]
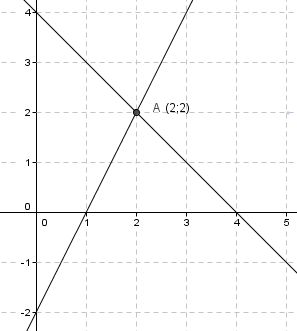
Le point d’intersection des deux droites a pour coordonnées(2;2).
Le couple solution du système est le couple(2;2).
Exercice n°1 : Résoudre graphiquement le système de deux équations a deux inconnues suivant :
y=-3x+3\\y=2x+\frac{1}{2}


