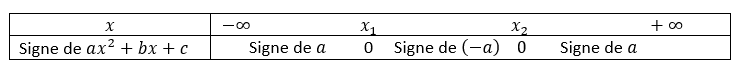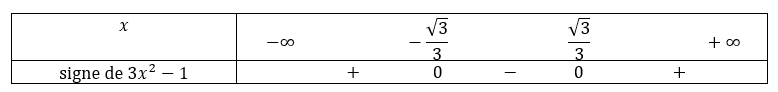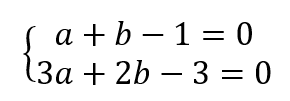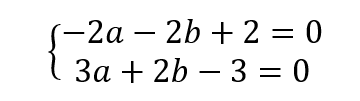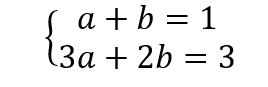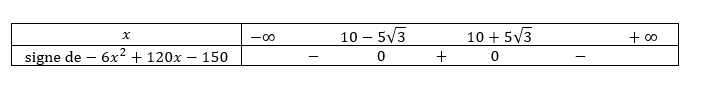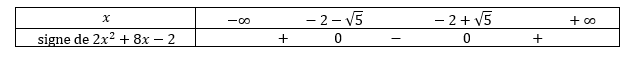Sommaire
Une page graphique de Géogébra pour conjecturer ou valider l’équation réduite de la tangente, tracer des courbes…
Pour déterminer l’équation réduite d’une tangente à, par exemple, la courbe de la fonction f définie sur \mathbf{R} par f(x)=x^2-2x+6 au point d’abscisse 2.
Saisir dans la colonne Algèbre située à gauche de l’écran : f(x)=x^2-2x+6.
Créer le point de la courbe d’abscisse 2 en cliquant sur le deuxième onglet en haut à partir de la gauche, sélectionner Point sur Objet et cliquer dans le repère sur le point de la courbe d’abscisse 2.
Tracer la tangente au point d’abscisse 2 en cliquant sur le quatrième onglet en haut à partir de la gauche, sélectionner Tangentes et cliquer dans le repère sur le point de la courbe d’abscisse 2 et puis sur la courbe. La tangente apparaît et dans la colonne Algèbre apparaît :
g : Tangente (A,f)
f(x)=2x+2.
Une page Calcul formel de Géogébra pour conjecturer ou valider un calcul de dérivée, le signe d’une quantité…
Exercice 1
On considère la fonction définie sur [0;+\infty[ par f(x)=x^3-3x^2-9x-1.
- On note f’ la fonction dérivée de f.
a. Montrer que pour x \in [0;+\infty[, f'(x)=3(x+1)(x-3).
b. En déduire le tableau de variation de f sur [0;+\infty[
c. Déterminer l’abscisse du point de la courbe représentative de f pour lequel le
coefficient directeur de la tangente vaut 36.
2. On note x_0 l’unique solution de l’équation 𝑓(𝑥) = 0. On admet que x_0\in[4;5].
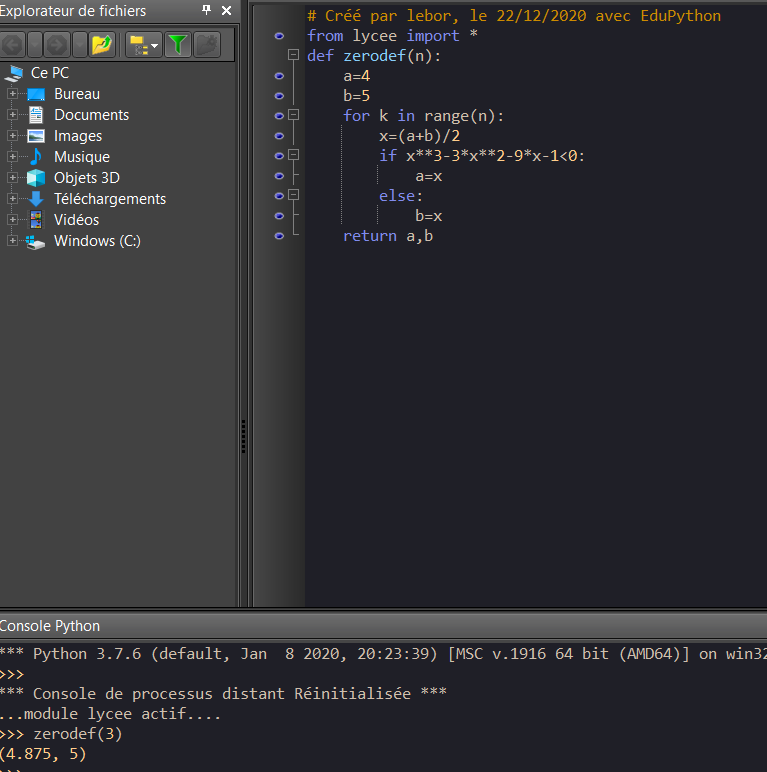
On considère la fonction suivante définie en langage Python.
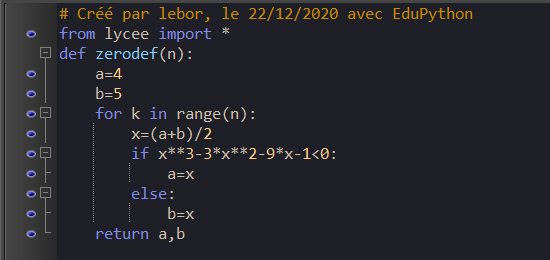
On applique cette fonction pour n=3. Reproduire sur la copie et compléter le
tableau suivant, jusqu’à l’arrêt de l’algorithme.
| x=\frac{a+b}{2} | f(x)<0? | a | b | Amplitude [a;b] | |
| k=0 | 4.5 | oui | 4.5 | 5 | 0.5 |
| k=1 | |||||
| k=2 |
b. En déduire un encadrement de x_0 , d’amplitude latex]0.125[/latex], par deux nombres
décimaux.
Exercice n°2
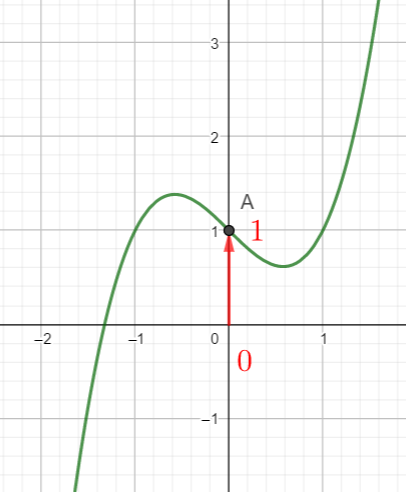
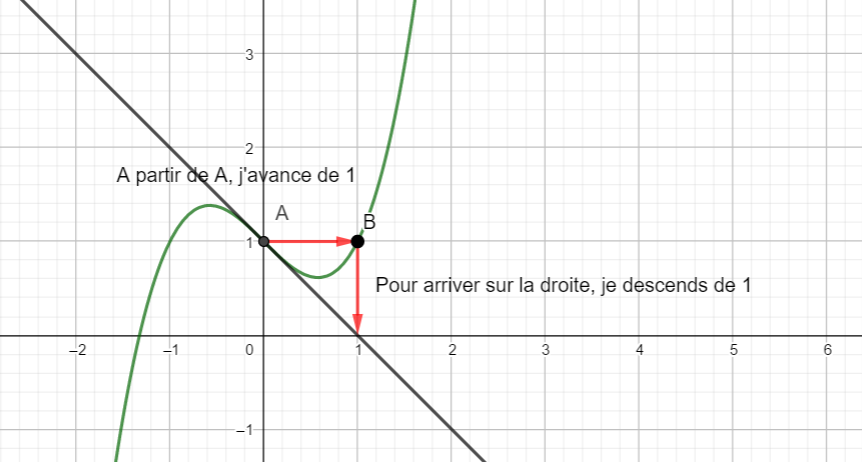
Dans la figure ci-dessous, on a tracé C_f, la courbe représentative d’une fonction f définie et
dérivable sur \mathbf{R} ainsi que les tangentes à C_f aux points A d’abscisse 0 et B d’abscisse 1.
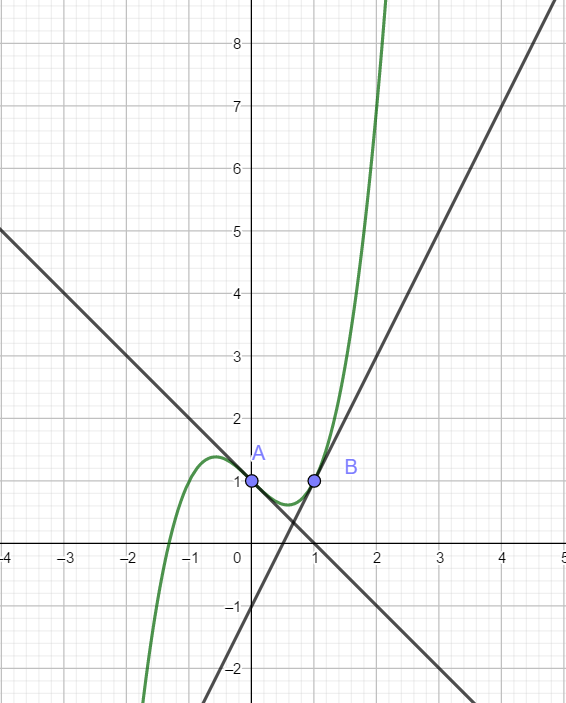
- Compléter le tableau de valeurs ci-dessous à l’aide de la courbe ci-dessus.
| x | 0 | 1 |
| f(x) | ||
| f'(x) |
On admet que la fonction 𝑓 est définie sur \mathbf{R} par :
f(x)=x^3-x+1.
2. a. Calculer f'(x).
b. Résoudre dans \mathbf{R} l’équation :f'(x) \geq 0.
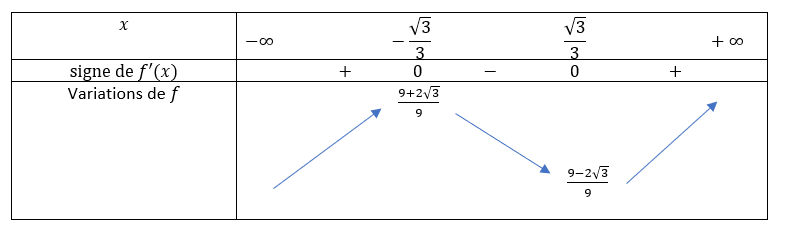
3. Dresser le tableau de variations de la fonction f sur \mathbf{R} .
4. Le point C(1;5) appartient-il à la tangente à la courbe représentative de 𝑓 au point
d’abscisse -1 ?
Exercice n°3
On s’intéresse à la consommation d’un véhicule roulant aux biocarburants en fonction de la vitesse de ce véhicule.
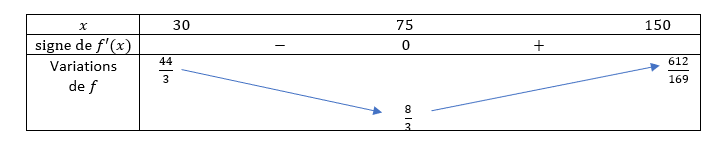
Cette consommation est modélisée par la fonction f définie sur [30;130] par :f(x)=\frac{8x^2-800x+30000}{x^2}
où x est exprimé en km/h et f (x) est exprimé en litres pour 100 km.
- Quelle est la consommation du véhicule s’il se déplace à 40 km.h^{-1}?
2. Pour quelle(s) vitesse(s) le véhicule consomme-t-il 4 litres pour 100 km ?
3. Pour quelle vitesse la consommation est-elle minimale ? Déterminer cette consommation minimale.
Exercice n°4
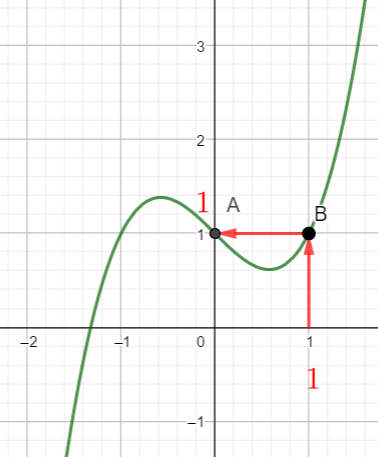
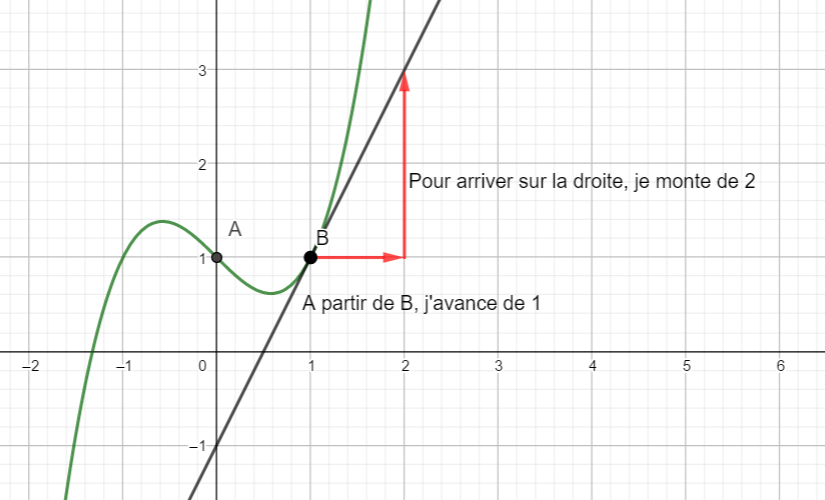
Dans la figure ci-dessous, on a tracé C_f, la courbe représentative d’une fonction f définie et dérivable sur \mathbf{R} ainsi que les tangentes à C_f aux points A d’abscisse 0 et B d’abscisse 1.
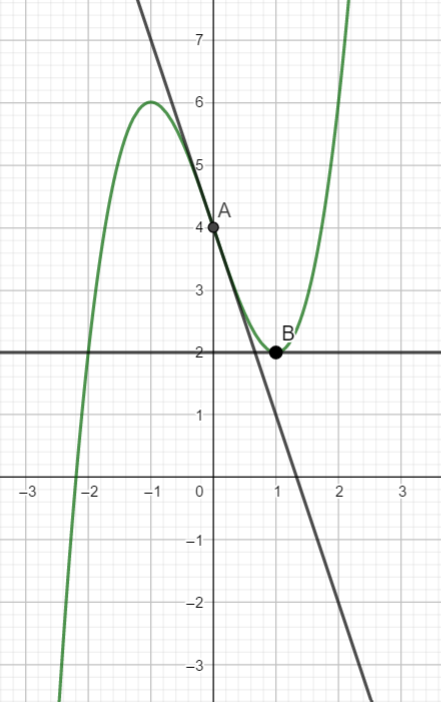
- Compléter le tableau de valeurs ci-dessous à l’aide de la courbe ci-dessus.
| x | 0 | 1 |
| f(x) | ||
| f'(x) |
On admet que la fonction 𝑓 est définie sur \mathbf{R} et peut s’écrire sous la forme
f(x)=ax^3+bx^2+cx+d.
2. a. Exprimer f'(x) en fonction de a, b, c, d.
b. Déterminer les valeurs des réels c et d.
c. Déterminer deux équations que vérifient les réels a et b
d. En déduire que f(x)=x^3-3x+4.
Exercice n°5
Le club de théâtre du Lycée Louis XIV a loué une grande salle de spectacle et organise une représentation de « Ubu Roi » d’Alfred Jarry.
Le prix de location de la salle est 4 500 euros.
Il espère avoir un maximum de spectateurs parmi la population des environs, aussi il décide de faire
passer des messages publicitaires sur la radio locale.
Soit x le nombre de jours de publicité. Pour x compris entre 0 et 20, la recette prévue est donnée par
f(x)=-2x^3+60x^2+2000.
Chaque jour de publicité est facturé 150 euros.
1. On fait un calcul sur 20 jours de publicité.
a. Quelle est la recette prévisible ?
b. Calculer les frais engagés : publicité et location
c. Calculer le bénéfice dans le cas où la recette est conforme à la prévision
2. Établir la formule donnant, en fonction du nombre x de jours de publicité, le montant total des
frais engagés qu’on notera C(x).
3. Combien de jours de publicité au minimum faut-il envisager pour que le bénéfice prévisible
soit positif ou nul ? On calculera le bénéfice réalisé pour 10 jours de publicité.
Exercice n°6
Partie A
On considère la fonction polynôme du second degré g définie sur \mathbf{R} par :
g(x)=x^2-5x+4
1) Résoudre l’équation g(x)=0.
2) Étudier le signe de g sur \mathbf{R}.
Partie B
On considère la fonction polynôme du troisième degré f définie sur \mathbf{R}par :
f(x)=2x^3-15x^2+24x
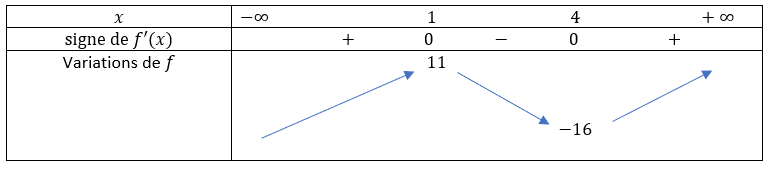
1) Calculer la dérivée f’ de f et vérifier que f'(x)=6g(x).
2) Etudier les variations de la fonction f.
3) Déterminer une équation de la tangente T à la courbe représentative de f au point B d’abscisse 3.
Exercice n°7
La fonction fest définie sur ]-2;+\infty[ par :
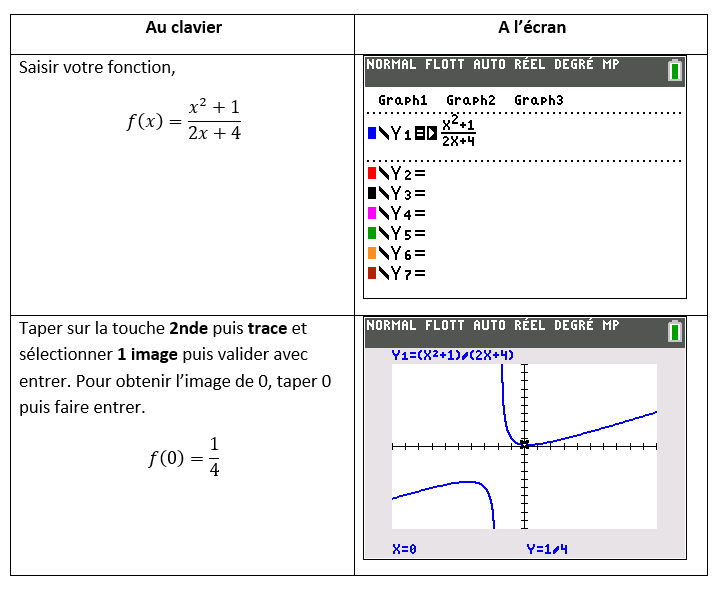
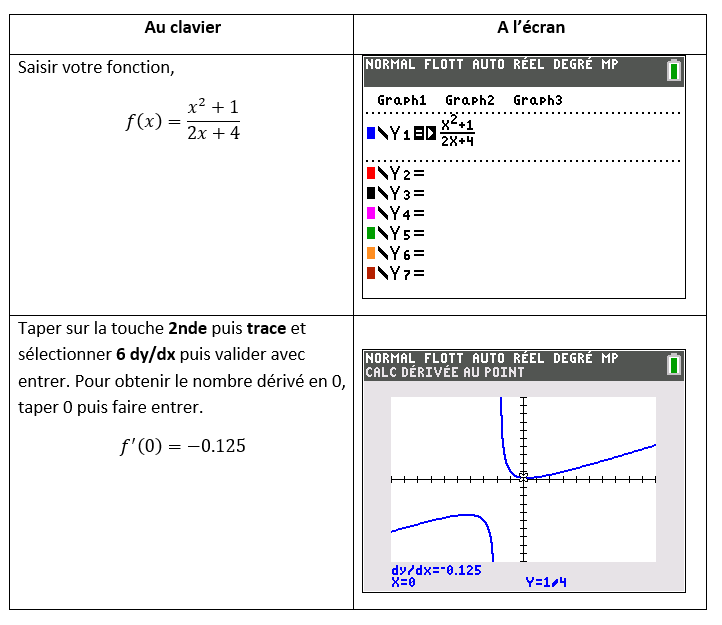
f(x)=\frac{x^2+1}{2x+4}
1) Démontrer que pour tout x appartenant à l’intervalle ]-2;+\infty[:
f'(x)=\frac{2x^2+8x-2}{(2x+4)^2}.
2) Déterminer le sens de variation de la fonction f sur ]-2;+\infty[.
3) Déterminer une équation de la tangente T à la courbe représentative de f au point d’abscisse 0.
4) Etudier la position relative de la courbe représentative de f et de la
droite d’équation y=x-2.
Exercice n°8
Une entreprise produit du tissu en coton. Celui-ci est fabriqué en 1 mètre de large et pour une
longueur x exprimée en kilomètre, x étant compris entre 0 et 10.
Le coût total de production en euros est donné en fonction de la longueur x
par la formule C(x)=15x^3-120x^2+500x+750.
1. a. Calculer le coût total de fabrication de 5 km de tissu.
b. Déterminer le coût moyen de fabrication d’un kilomètre de tissu lorsqu’on fabrique
5 km de tissu.
2. On rappelle que le coût moyen de production C_{M}(x) mesure le coût par unité produite.
On considère la fonction C_{M} définie sur l’intervalle ]0;10] par C_{M}(x)=\frac{C(x)}{x}=15x^2-120x+500+\frac{750}{x} .
a. Montrer que C_{M}'(x)=\frac{30(x-5)(x^2+x+5)}{x^2}
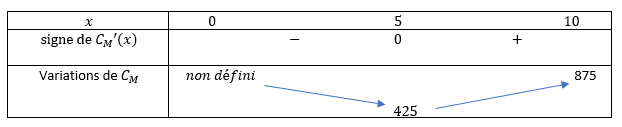
b. Étudier le signe de C_{M}'(x) et dresser le tableau de variation de la fonction C_{M} sur
l’intervalle ]0;10] .
c. Quel est le coût moyen minimal et pour combien de kilomètres de tissu est-il obtenu est-il obtenu ?
Exercice n°9
On considère la fonction définie sur [0;+\infty[ par f(x)=x^3+3x^2+3x+2.
- a. Montrer que pour x \in [0;+\infty[, f(x)=(x+2)(x^2+2x+1).
b. En déduire que C la courbe de f coupe l’axe des abscisses en un seul point.
2.a. Calculer f'(x) et montrer que f'(x)=3(x+1)^2.
2.b. Dresser le tableau de variations de f sur [0;+\infty[.
3. Déterminer l’équation de la tangente T à la courbe de f au point d’abscisse 0. Le point de coordonnées (-3;-7) appartient-il à T?