1. Equations de tangentes. Exercices.

ANALYSE, Dérivation, Equation réduite d'une tangente à une courbe en un point, Niveau première

Une page de Géogébra pour conjecturer ou valider l’équation réduite de la tangente.

Pour déterminer l’équation réduite d’une tangente à, par exemple, la courbe de la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^2-2x+6$ au point d’abscisse $2$ .

Saisir dans la colonne Algèbre située à gauche de l’écran : $f(x)=x^2-2x+6$ .

Créer le point de la courbe d’abscisse $2$ en cliquant sur le deuxième onglet en haut à partir de la gauche, sélectionner Point sur Objet et cliquer dans le repère sur le point de la courbe d’abscisse 2.

Tracer la tangente au point d’abscisse $2$ en cliquant sur le quatrième onglet en haut à partir de la gauche, sélectionner Tangentes et cliquer dans le repère sur le point de la courbe d’abscisse 2 et puis sur la courbe. La tangente apparaît et dans la colonne Algèbre apparaît :

g : Tangente (A,f)

$f(x)=2x+2$ .

Une page de calcul formel pour conjecturer ou valider le calcul de la dérivée.

Pour calculer, par exemple, la dérivée de la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^2-2x+6$ .

Saisir sur la ligne 1: $f(x)=x^2-2x+6$ .

Cliquer sur le neuvième onglet en haut à partir de la gauche.

Apparaît alors Dérivée: $f'(x)=2x-2$ .

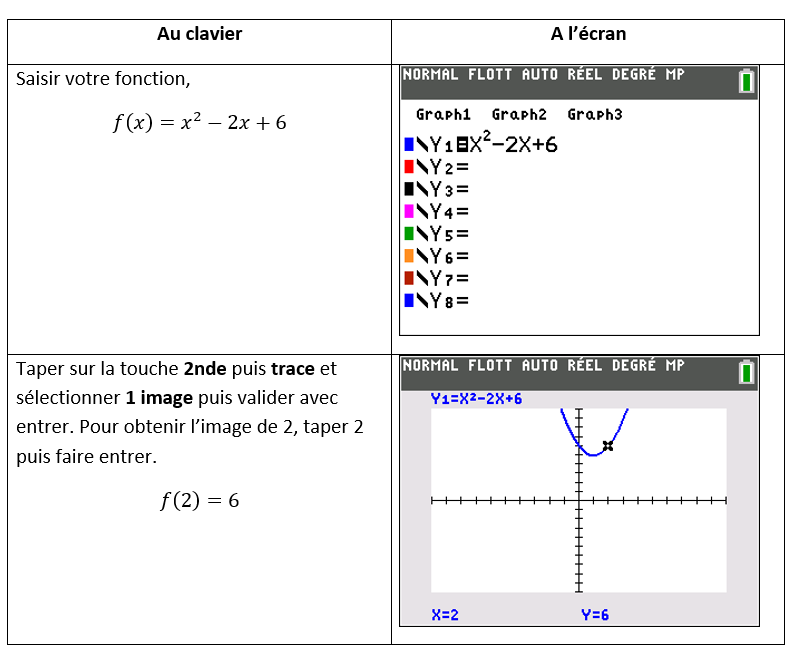
Pour déterminer l’image d’un nombre avec la calculatrice TI-83 Premium CE

Par exemple, déterminer $f(2)$ avec la calculatrice TI-83 Premium CE quand $f(x)=x^2-2x+6$ .

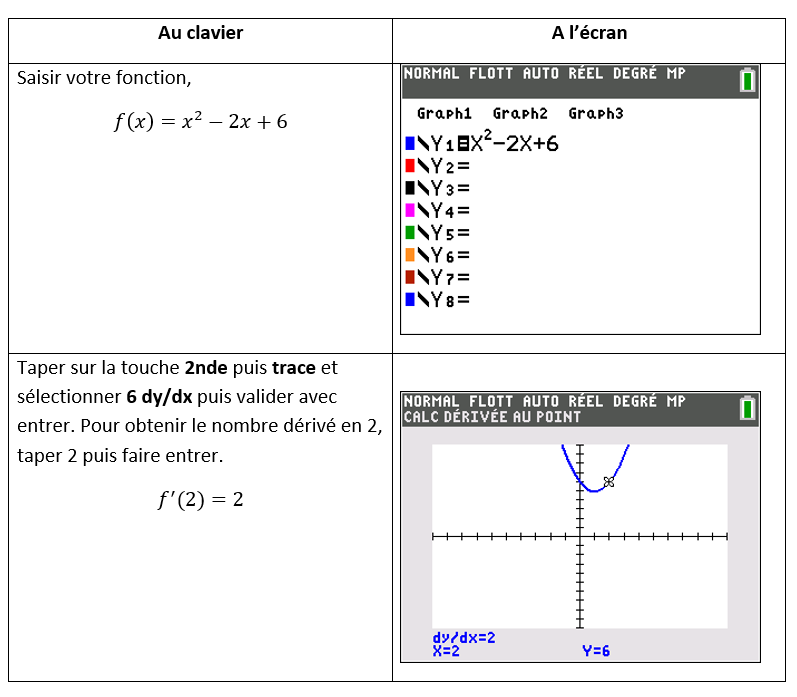
Pour déterminer un nombre dérivé avec la calculatrice TI-83 Premium CE

Par exemple, déterminer $f'(2)$ avec la calculatrice TI-83 Premium CE quand $f(x)=x^2-2x+6$ .

Exercice n°1:

Soit la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^2-2x+6$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $2$ .

Calculer $f(2)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(2)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $2$ .

Exercice n°2:

Soit la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^2-5x+4$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $1$ .

Calculer $f(1)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(1)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $1$ .

Exercice n°3:

Soit la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^3-5x+4$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $0$ .

Calculer $f(0)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(0)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $0$ .

Exercice n°4:

Soit la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=x^3-x^2+4$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $-1$ .

Calculer $f(-1)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(-1)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $-1$ .

Exercice n°5:

Soit la fonction $f$ définie sur $\mathbf{R}$ par $f(x)=2x^3-2x^2+6x$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $1$ .

Calculer $f(1)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(1)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $1$ .

Exercice n°6:

Soit la fonction $f$ définie sur $[0;+\infty[$ par $f(x)=x^2\sqrt{x}$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $2$ .

Calculer $f(2)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(2)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $2$ .

Exercice n°7:

Soit la fonction $f$ définie sur $[0;+\infty[$ par $f(x)=\sqrt{x}(2x+1)$ .

On se propose de déterminer l’équation de la tangente au point de la courbe d’abscisse $1$ .

Calculer $f(1)$ .

2.a. Calculer $f'(x)$

2.b. Calculer $f'(1)$

3. En déduire l’équation réduite de la tangente à la courbe au point d’abscisse $1$ .

$f(x)= x^2\sqrt{x}$ est dérivable sur $]0;+\infty[$

1.On veut calculer $f'(x)$ .

On répond à la question suivante : $f(x)$ est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions $u\times v$ avec $u(x)=x^2$ et $v(x)=\sqrt{x}$ .

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

$f(x)$ est	$f'(x)$ se calcule ainsi :
une somme $u+v$	$u’+v’$
le produit d’une constante $k$ par une fonction $u$ c’est-à-dire $ku$	$k\times u’$
un produit de deux fonctions $u\times v$	$u’\times v+u\times v’$
l’inverse d’une fonction $\frac{1}{u}$	$-\frac{u’}{u^2}$
un quotient $\frac{u}{v}$	$\frac{u’\times v-u\times v’}{v^2}$

2a.on veut calculer la dérivée $u'(x)$

$u(x)=x^2$ est une fonction de référence, on utilise la ligne carré du tableau n°2 ci-dessous

$u'(x)=2x$

2b.on veut calculer la dérivée $v'(x)$

$v(x)=\sqrt{x}$ est une fonction de référence, on utilise la ligne racine carrée du tableau n°2 ci-dessous

$v'(x)=\frac{1}{2\sqrt{x}}$

Fonction	$f(x)$	Dérivable sur…	$f'(x)$
constante	$f(x)=k$	$\mathbf{R}$	$f'(x)=0$
identité	$f(x)=x$	$\mathbf{R}$	$f'(x)=1$
carré	$f(x)=x^2$	$\mathbf{R}$	$f'(x)=2x$
cube	$f(x)=x^3$	$\mathbf{R}$	$f'(x)=3x^2$
inverse	$f(x)=\frac{1}{x}$	$\left]-\infty;0\right[\cup\left]0;+\infty\right[$	$f'(x)=-\frac{1}{x^2}$
racine carrée	$f(x)=\sqrt{x}$	$]0;+\infty[$	$f'(x)=\frac{1}{2\sqrt{x}}$

3. On calcule la dérivée $f'(x)$

On remplace $u$ par $x^2$ , $v$ par $\sqrt{x}$ , $u’$ par $2x$ et $v’$ par $\frac{1}{2\sqrt{x}}$ dans la formule $u’\times v+u\times v’$

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (x^2\sqrt{x})’\\f'(x)=(x^2)’\times{\sqrt{x}}+x^2\times{\sqrt{x}’} \\f'(x)=2x\times {\sqrt{x}}+{x^2}\times{\frac{1}{2\sqrt{x}}} \\f'(x)=2x\sqrt{x}+\frac{x^2}{2\sqrt{x}}

On peut s’arrêter là, on pourra utiliser cette forme pour calculer $f'(2)$ …Pour les plus curieux, poursuivez !

On peut simplifier le deuxième terme de la somme par $\sqrt{x}$

f'(x)=2x\sqrt{x}+\frac{x\sqrt{x}}{2}

On met au même dénominateur, ici 2.

f'(x)=2x\sqrt{x}\times{\frac{2}{2} }+\frac{x\sqrt{x}}{2} \\f'(x)=\frac{4x\sqrt{x}+x\sqrt{x}}{2}  \\f'(x)=\frac{5x\sqrt{x}}{2}

$f(x)= \sqrt{x}(2x+1)$ est dérivable sur $]0;+\infty[$

1.On veut calculer $f'(x)$ .

On répond à la question suivante : $f(x)$ est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions $u\times v$ avec $u(x)=\sqrt{x}$ et $v(x)=2x+1$ .

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

$f(x)$ est	$f'(x)$ se calcule ainsi :
une somme $u+v$	$u’+v’$
le produit d’une constante $k$ par une fonction $u$ c’est-à-dire $ku$	$k\times u’$
un produit de deux fonctions $u\times v$	$u’\times v+u\times v’$
l’inverse d’une fonction $\frac{1}{u}$	$-\frac{u’}{u^2}$
un quotient $\frac{u}{v}$	$\frac{u’\times v-u\times v’}{v^2}$

2a.on veut calculer la dérivée $u'(x)$

$u(x)=\sqrt{x}$ est une fonction de référence, on utilise la ligne racine carrée du second tableau

$u'(x)=\frac{1}{2\sqrt{x}}$

2b.on veut calculer la dérivée $v'(x)$

$v(x)=2x+1$ est une somme, on utilise la ligne n°1 du premier tableau

$v'(x)=(2x+1)’$

$\hspace{0.9cm}=(2x)’+(1)’$

$\hspace{0.9cm}=2(x)’+0$

$\hspace{0.9cm}=2\times1$

$\hspace{0.9cm}=2$

Fonction	$f(x)$	Dérivable sur…	$f'(x)$
constante	$f(x)=k$	$\mathbf{R}$	$f'(x)=0$
identité	$f(x)=x$	$\mathbf{R}$	$f'(x)=1$
carré	$f(x)=x^2$	$\mathbf{R}$	$f'(x)=2x$
cube	$f(x)=x^3$	$\mathbf{R}$	$f'(x)=3x^2$
inverse	$f(x)=\frac{1}{x}$	$\left]-\infty;0\right[\cup\left]0;+\infty\right[$	$f'(x)=-\frac{1}{x^2}$
racine carrée	$f(x)=\sqrt{x}$	$]0;+\infty[$	$f'(x)=\frac{1}{2\sqrt{x}}$

3. On calcule la dérivée $f'(x)$

On remplace $u$ par $\sqrt{x}$ , $v$ par $2x+1$ , $u’$ par $\frac{1}{2\sqrt{x}}$ et $v’$ par $2$ dans la formule $u’\times v+u\times v’$

Voilà ce qu’il faut écrire sur votre copie :

f'(x)=( \sqrt{x}(2x+1))’\\f'(x)=\sqrt{x}’\times{(2x+1)}+\sqrt{x}\times{(2x+1)’} \\f'(x)=\frac{1}{2\sqrt{x}}\times{(2x+1)}+\sqrt{x}\times{2} \\f'(x)=\frac{2x+1}{2\sqrt{x}}+2\sqrt{x}

On peut s’arrêter là..

1. Equations de tangentes. Exercices.

Sommaire

Une page de Géogébra pour conjecturer ou valider l’équation réduite de la tangente.

Une page de calcul formel pour conjecturer ou valider le calcul de la dérivée.

Pour déterminer l’image d’un nombre avec la calculatrice TI-83 Premium CE

Pour déterminer un nombre dérivé avec la calculatrice TI-83 Premium CE

Exercice n°1:

Exercice n°2:

Exercice n°3:

Exercice n°4:

Exercice n°5:

Exercice n°6:

Exercice n°7: