Sommaire
Exercice n°1
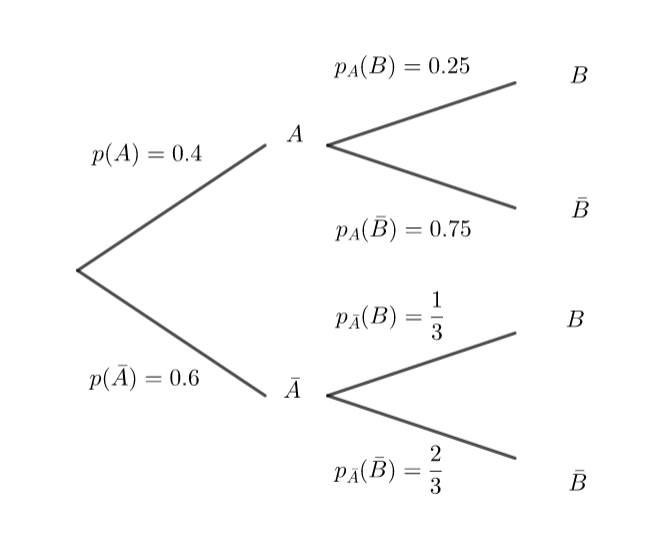
A et B sont deux évènements d’un univers \Omega
A | \bar A | TOTAL | |
B | 10\% | 20\% | 30\% |
\bar B | 30\% | 40\% | 70\% |
TOTAL | 40\% | 60\% | 100\% |
- En utilisant le tableau précédent, donner les probabilités suivantes
p(A), p(\bar A), p(A\cap B), p(\bar A\cap \bar B), p_A(B) et p_{\bar A}(\bar B)
2. Reproduire et compléter l’arbre pondéré ci-dessous .
Exercice n°2
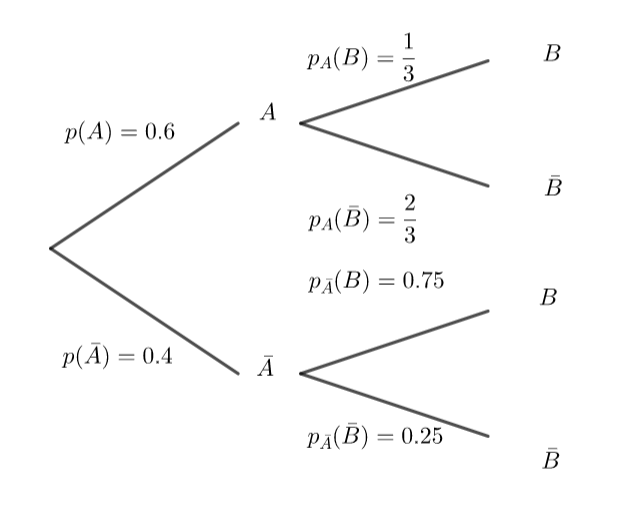
A et B sont deux évènements d’un univers \Omega
A | \bar A | TOTAL | |
B | 20\% | 30\% | 50\% |
\bar B | 40\% | 10\% | 50\% |
TOTAL | 60\% | 40\% | 100\% |
- En utilisant le tableau précédent, donner les probabilités suivantes
p(A), p(\bar A), p(A\cap B), p(\bar A\cap \bar B), p_A(B) et p_{\bar A}(\bar B)
2. Reproduire et compléter l’arbre pondéré ci-dessous .

Exercice n°3
A et B sont deux évènements d’un univers \Omega
Voici un arbre pondéré:
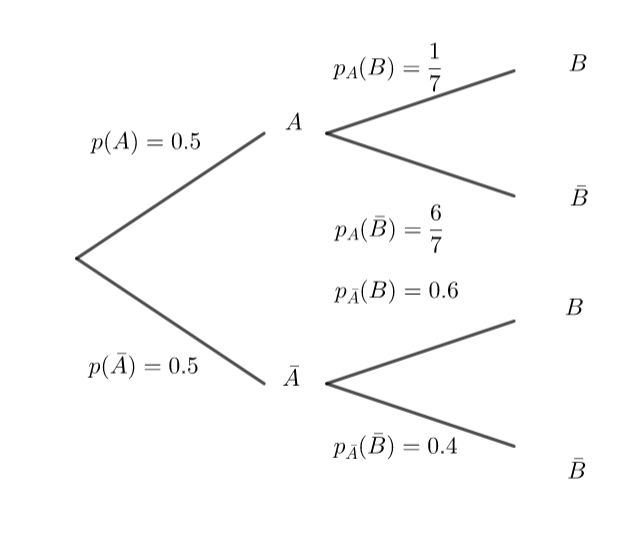
- Calculer p(A\cap B), p(A\cap \bar B), p(\bar A\cap B) et p(\bar A\cap \bar B).
2. Reproduire et compléter le tableau ci-dessous :
A | \bar A | TOTAL | |
B | |||
\bar B | |||
TOTAL | 1 |
Exercice n°4
A et B sont deux évènements d’un univers \Omega
Voici un arbre pondéré:
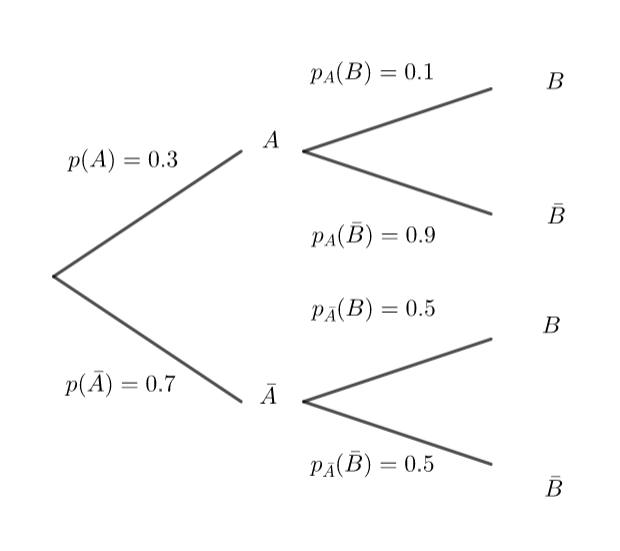
- Calculer p(A\cap B), p(A\cap \bar B), p(\bar A\cap B) et p(\bar A\cap \bar B).
2. Reproduire et compléter le tableau ci-dessous :
A | \bar A | TOTAL | |
B | |||
\bar B | |||
TOTAL | 1 |
Exercice n°5
A et B sont deux évènements d’un univers \Omega. p(A)=0.4 , p(B)=0.5 et p(A\cup B)=0.7
- Calculer p(A\cap B).
2. Les évènements A et B sont-ils incompatibles ?
3. Les évènements A et B sont-ils indépendants ?
Exercice n°6
A, B, C, D sont quatre évènements d’un univers \Omega
Voici un arbre pondéré:
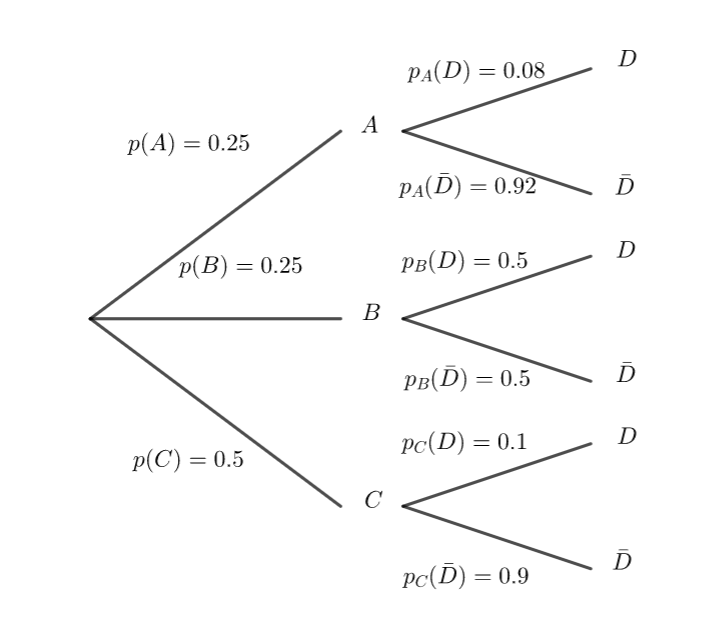
- Calculer p(A\cap D).
2. Calculer p( D).
3. Calculer p_D(A).
Exercice n°7
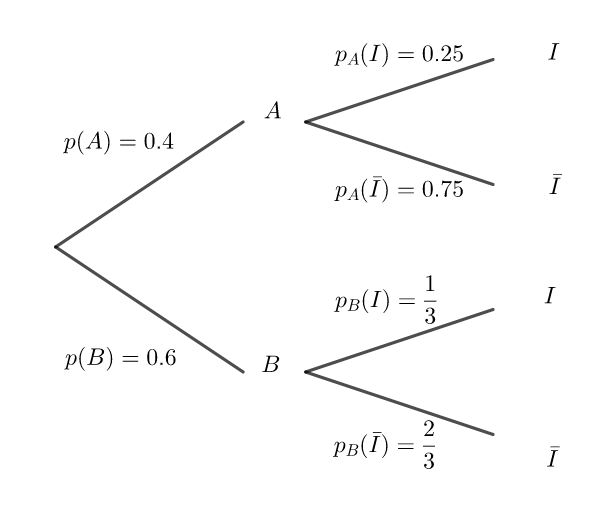
Une entreprise dispose d’un stock de guirlandes électriques. On sait que 40 % des guirlandes proviennent d’un fournisseur A et le reste d’un fournisseur B.
Un quart des guirlandes provenant du fournisseur A et un tiers des guirlandes provenant du fournisseur B peuvent être utilisées uniquement en intérieur pour des raisons de sécurité. Les autres
guirlandes peuvent être utilisées aussi bien en intérieur qu’en extérieur.
On choisit au hasard une guirlande dans le stock.
• On note A l’évènement « la guirlande provient du fournisseur A » et B l’évènement « la
guirlande provient du fournisseur B ».
• On note I l’évènement « la guirlande peut être utilisée uniquement en intérieur ».
1. Reproduire et compléter l’arbre pondéré ci-dessous.
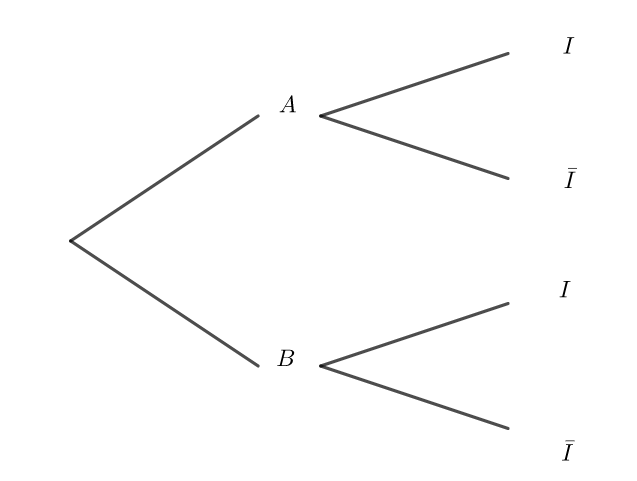
2. Montrer que la probabilité p(I) de l’évènement I est 0,3.
3. On choisit une guirlande pouvant être utilisée aussi bien en intérieur qu’en extérieur. Le
responsable de l’entreprise estime qu’il y a autant de chance qu’elle provienne du fournisseur A que du fournisseur B.
Le responsable a-t-il raison ? Justifier.
Exercice n°8
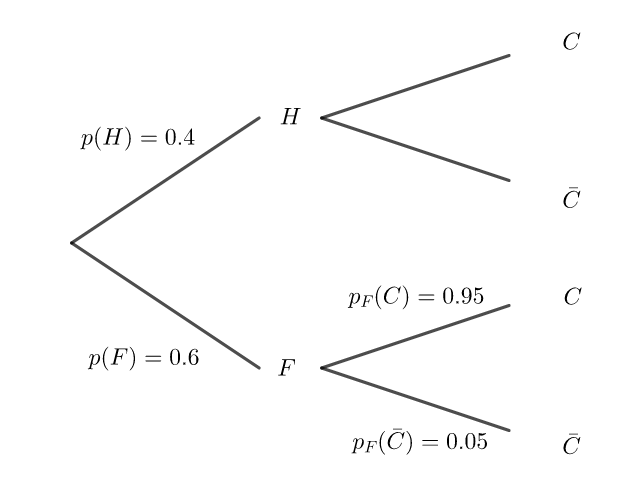
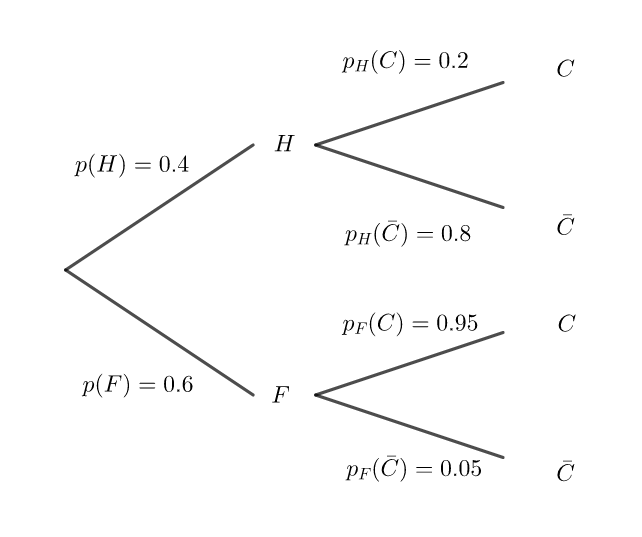
Un club de remise en forme propose, outre l’accès aux salles de musculation, des cours collectifs pour lesquels un supplément est demandé lors de l’inscription. Une fiche identifie chaque membre et son type d’abonnement : avec ou sans cours collectif.
Une étude sur les profils des membres de ce club a montré que :
40 % des membres sont des hommes.
65 % des membres sont inscrits aux cours collectifs.
Parmi les femmes, membres de ce club, seulement 5 % ne sont pas inscrites aux cours collectifs.
On choisit une fiche au hasard et on considère les évènements suivants :
— H : « la fiche est celle d’un homme »,
— F : « la fiche est celle d’une femme »,
— C : « la fiche est celle d’un membre inscrit à des cours collectifs ».
Rappel de notation : Si A et B sont deux évènements donnés, p(A) désigne la probabilité de A et
p_B(A) désigne la probabilité conditionnelle de A sachant B.
1. Préciser les probabilités suivantes : p(H) , p_F(\bar{C}) et p_F(C) puis les reporter sur l’arbre pondéré ci-dessous qu’on complètera au fur et à mesure.
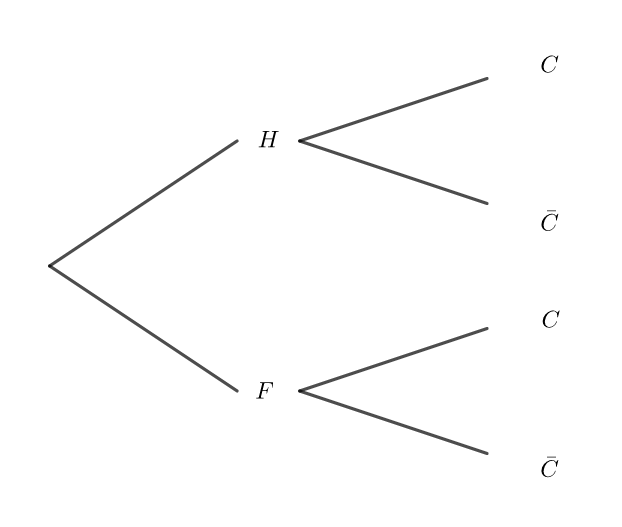
2. a. Déterminer p(F ∩C).
b. Montrer que p(H ∩C) = 0,08.
c. On tire la fiche d’un homme, quelle est la probabilité que celui-ci soit inscrit aux cours
collectifs ?
d. Compléter l’arbre pondéré de la question 1.