Définition
Soit X la variable aléatoire définie sur un univers \Omega et à valeurs dans \{1;2;3;…n\}.
On dit que X suit la loi uniforme sur \{1;2;3;…n\} si p(X=k)=\frac{1}{n} pour tout k \in \{1;2;3;…n\}
Remarque : ici les valeurs prises par X sont des valeurs isolées ( ici des nombres entiers) , on dit que X suit une loi discrète.
Propriété
Soit X la variable aléatoire qui suit la loi uniforme sur \{1;2;3;…n\}.
L’ espérance de X vérifie E(x)=\frac{n+1}{2}.
Démonstration de la propriété
Exercice n°1 :
Dans un bar, le serveur a remarqué qu’un de ses clients boit de façon équiprobable entre 1 et 5 cafés par jour.
- Donner la loi suivie par la variable aléatoire X donnant le nombre de cafés bus par jour par le client.
2. Calculer l’espérance de X. Interpréter le résultat.
Exercice n°2
Dans une urne, il y a 9 boules.
- Trois sont vertes et portent le n°2
- Deux sont rouges et portent le n°1
- Quatre sont bleues : trois sont numérotées 3 et une porte le numéro 1.
On considère la variable aléatoire X qui associe à la boule tirée le numéro lu sur la boule.
- Donner la loi suivie par la variable aléatoire X. Quelle est la nature de cette loi ?
2. Calculer l’espérance de X.
Exercice n°3 :
Une roue de loterie bien équilibrée est partagée en 6 parties égales. Chaque secteur est numéroté.
On fait tourner la roue.
Soit X la variable aléatoire qui prend la valeur indiquée sur le secteur angulaire quand la roue s’arrête.
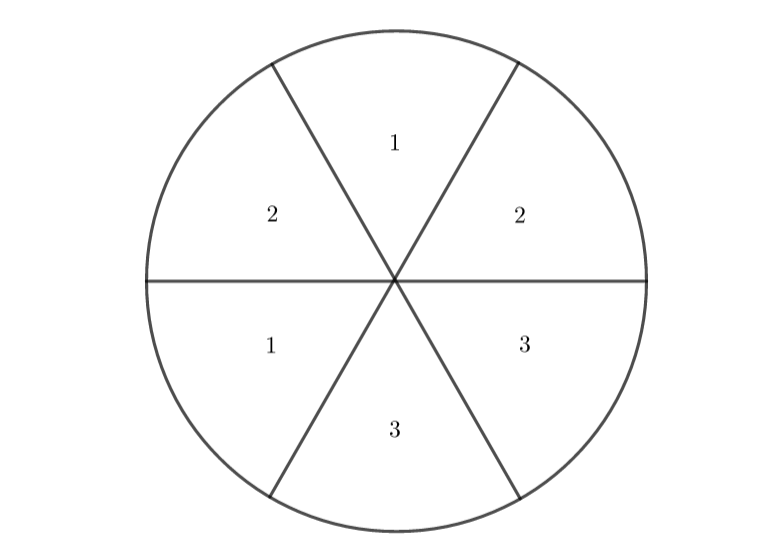
- Donner la loi suivie par la variable aléatoire X.
2. Combien de points un joueur peut-il espérer gagner en moyenne au cours d’une partie.
3. Pour pouvoir jouer, on doit miser 1 euro. Chaque point rapporte 40 centimes. le jeu est-il équitable ?