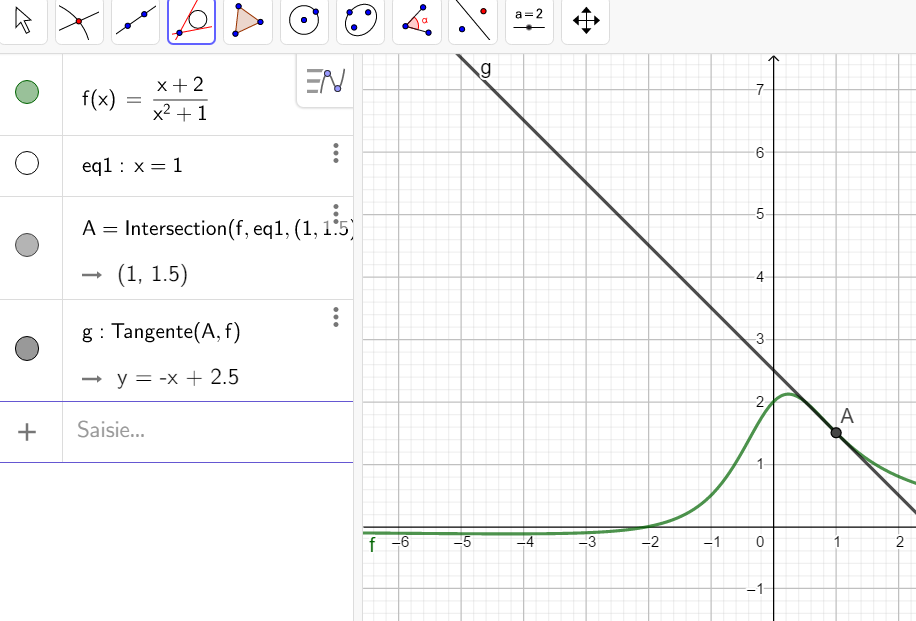
Déterminer par le calcul l’équation de la tangente à la courbe de la fonction f définie sur \mathbf{R} par
f(x)=\frac{x+2}{x^2+1} au point d’abscisse 1.
1.Je calcule f(1) en remplaçant tous les x par 1 dans
f(x)=\frac{x+2}{x^2+1}
f(1)=\frac{1+2}{1^2+1}\hspace{0.8cm}=\frac{3}{1+1}
\hspace{0.8cm}=\frac{3}{2}
Je vérifie le résultat de f(1) à la calculatrice
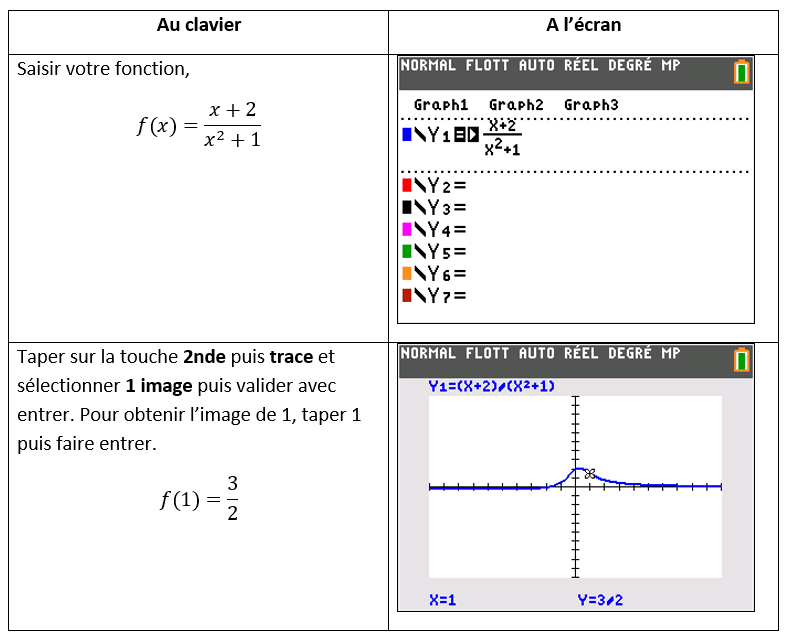
2.a.Je calcule f'(x)
f(x)=\frac{x+2}{x^2+1} est le quotient de deux fonctions , donc :
f'(x)=\frac{(x+2)'(x^2+1)-(x+2)(x^2+1)’}{(x^2+1)^2}\\ \hspace{0.8cm}=\frac{1\times (x^2+1)-(x+2)\times 2x}{(x^2+1)^2}\\ \hspace{0.8cm}=\frac{ (x^2+1)-(2x^2+4x)}{(x^2+1)^2}\\ \hspace{0.8cm}=\frac{ x^2+1-2x^2-4x}{(x^2+1)^2}\\ \hspace{0.8cm}=\frac{- x^2-4x+1}{(x^2+1)^2}2.b.Puis on calcule f'(1) en remplaçant tous les x par 1 dans f'(x)=\frac{- x^2-4x+1}{(x^2+1)^2}
f'(1)=\frac{- 1^2-4\times 1+1}{(1^2+1)^2}
\hspace{0.8cm}=\frac{-1-4+1}{(1+1)^2}
\hspace{0.8cm}=\frac{-4}{2^2}
\hspace{0.8cm}=\frac{-4}{4}
\hspace{0.8cm}=-1
Je vérifie le résultat de f'(1) à la calculatrice
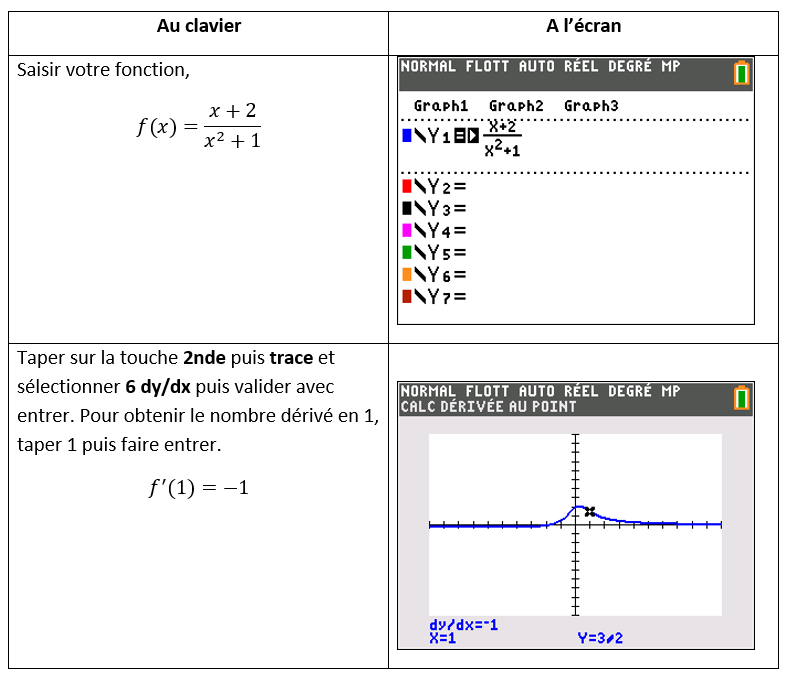
3.Je remplace a,f(a),f'(a) par 1,\frac{3}{2},(-1) dans y=f'(a)(x-a)+f(a)
y=(-1)(x-1)+\frac{3}{2}
y=-x+1+\frac{3}{2}
y=-x+\frac{2}{2}+\frac{3}{2}
y=-x+\frac{5}{2}
4.Je valide avec Géogébra.