logo

Exercice corrigé : somme de vecteurs.Niveau seconde.

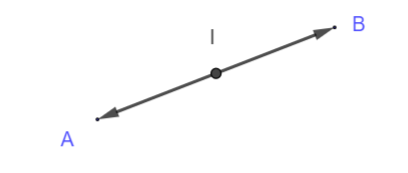
Exercice n°2

 Soient  A(4;2) et B(-2;6).

  1. Calculer les coordonnées de I le milieu de [AB] (utiliser la formule vue dans la partie coordonnées d’un point).

Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du milieu I en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le deuxième onglet en partant de la gauche et on sélectionne Milieu ou centre dans le menu déroulant. Dans le repère on clique gauche  sur le point A et sur le point B, le logiciel nomme le milieu C. Pour le renommer on clique droit sur C et on sélectionne Renommer dans le menu déroulant. On renomme le point avec la lettre I. On lit ses coordonnées dans la colonne Algèbre.

correction

2.a.Calculer les coordonnées du vecteur  \overrightarrow{IA}.

Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du vecteurs \overrightarrow{IA} en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le troisième onglet en partant de la gauche et on sélectionne Vecteur dans le menu déroulant. Dans le repère on clique gauche  sur le point I et sur le point A.  On lit ses coordonnées dans la colonne Algèbre.

correction

2.b.Calculer les coordonnées du vecteur  \overrightarrow{IB}.

Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du vecteurs \overrightarrow{IB} en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le troisième onglet en partant de la gauche et on sélectionne Vecteur dans le menu déroulant. Dans le repère on clique gauche  sur le point I et sur le point B.  On lit ses coordonnées dans la colonne Algèbre.

correction

2.c. Calculer les coordonnées du vecteur \overrightarrow{IA} +\overrightarrow{IB}.

correction

2.d. Le résultat de la question 2.c. vous semble-t-il cohérent ?

correction

©2020 – Math’O karé SAS

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(4;2) \hspace{0.4cm} B(-2;6)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {4+(-2)}{2}\hspace {2cm}y_I=\frac {2+6}{2}

x_I=\frac {2}{2}\hspace {2cm}y_I=\frac {8}{2}

x_I=1\hspace {2cm}y_I=4

Donc I(1;4)

Pour déterminer les coordonnées du vecteur \overrightarrow{IA}.

Je repère les coordonnées des points I et A.

\hspace{2.1cm}x_{I}\hspace{0.2cm}y_{I}\hspace{2cm}x_{A}\hspace{0.2cm}y_{A}

\hspace{1.8cm}I(1;4)\hspace{2cm}A(4;2)

J’écris la formule : \overrightarrow{IA}(x_{A}-x_{I};y_{A}-y_{I})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{IA}(4-1;2-4)

\overrightarrow{IA}(3;-2)

 

Pour déterminer les coordonnées du vecteur \overrightarrow{IB}.

Je repère les coordonnées des points I et B.

\hspace{2.1cm}x_{I}\hspace{0.2cm}y_{I}\hspace{2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}I(1;4)\hspace{2cm}B(-2;6)

J’écris la formule : \overrightarrow{IB}(x_{B}-x_{I};y_{B}-y_{I})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{IB}((-2)-1;6-4)

\overrightarrow{IB}(-3;2)

\hspace{0.6cm}\overrightarrow{IA}(3;-2)\\\hspace{0.6cm}\overrightarrow{IB}(-3;2)

Donc \overrightarrow{IA}+\overrightarrow{IB}(3+(-3);-2+2)

Donc \overrightarrow{IA}+\overrightarrow{IB}(0;0)

Comme I est le milieu de [AB] les vecteurs \overrightarrow{IA} et \overrightarrow{IB} sont opposés donc leur somme est égale au vecteur nul, \vec{0}.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.