La droite est définie par deux points A (5;3) et B(-1;6)
METHODE N°1:
Déterminer par le calcul une équation cartésienne de la droite (AB) où A(5;3) et B(-1;6) .
Il s’agit de déterminer une relation du type ax+by+c=0 vérifiée par les coordonnées (x;y) d’un point quelconque de la droite (AB) que l’on va nommer M . La figure géométrique suivante traduit la situation qui nous intéresse.
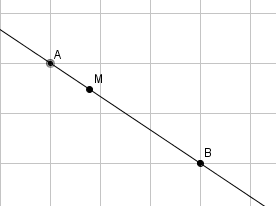
Pour caractériser la situation géométrique ci-dessus, nous allons utiliser trois langages différents : le langage des points et des droites, le langage des vecteurs et celui des coordonnées.
Langage des points et des droites
Langage des vecteurs
Langage des coordonnées
Les trois points A, B , M sont alignés.
Les vecteurs \overrightarrow {AB} et \overrightarrow {AM} sont colinéaires.
ou
Les vecteurs \overrightarrow {BA} et \overrightarrow {BM} sont colinéaires.
ou
Les vecteurs \overrightarrow {MA} et \overrightarrow {MB} sont colinéaires.
Les coordonnées des vecteurs \overrightarrow {AB} et \overrightarrow {AM} sont proportionnelles c’est-à-dire que det(\overrightarrow{AB};\overrightarrow{AM}) =0
ou
Les coordonnées des vecteurs \overrightarrow {BA} et \overrightarrow {BM} sont proportionnelles c’est-à-dire que det(\overrightarrow{BA};\overrightarrow{BM}) =0
ou
Les coordonnées des vecteurs \overrightarrow {MA} et \overrightarrow {MB} sont proportionnelles c’est-à-dire que det(\overrightarrow{MA};\overrightarrow{MB}) =0 .
1)On calcule les coordonnées du vecteur \overrightarrow{AB}
On n’hésite pas à repérer les coordonnées des points A et B ainsi
\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}
\hspace{0.2cm} A(5;3) \hspace{0.4cm} B(-1;6)
On calcule les coordonnées du vecteur \overrightarrow{AB} (x_{B}-x_{A};y_{B}-y_{A})
Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.
\hspace{4.5cm}\overrightarrow{AB} ((-1)-5;6-3) \hspace{4.5cm}\overrightarrow{AB} (-6;3)2) On calcule les coordonnées du vecteur \overrightarrow{AM}
On n’hésite pas à repérer les coordonnées des points A et M ainsi
\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{M} y_{M}
\hspace{0.2cm} A(5;3) \hspace{0.4cm} M(x;y)
On calcule les coordonnées du vecteur \overrightarrow{AM} (x_{M}-x_{A};y_{M}-y_{A})
Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.
\hspace{4.5cm}\overrightarrow{AM} (x-5;y-3)3) Je calcule le déterminant des deux vecteurs \overrightarrow{AB} et \overrightarrow{AM}
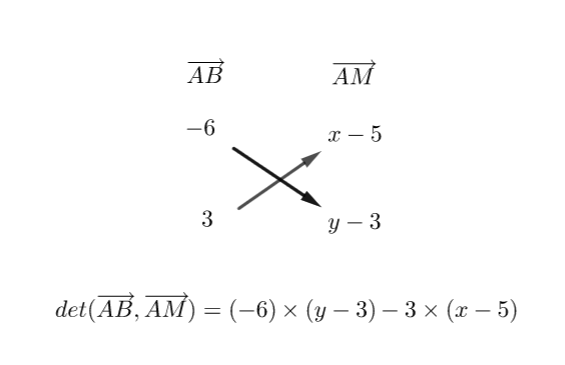
J’utilise la distributivité de la multiplication par rapport à l’addition pour développer les deux produits.
det(\overrightarrow{AB};\overrightarrow{AM}) =-6y+18-3x+15Je réduis la somme en ajoutant 18 et 15
det(\overrightarrow{AB};\overrightarrow{AM}) =-6y-3x+334) J’écris une équation cartésienne de la droite (AB)
Comme le déterminant des deux vecteurs \overrightarrow{AB} et \overrightarrow{AM} est nul alors -6y-3x+33=0. On prend soin de réécrire l’égalité en placant les x avant les y.
la droite (AB) admet -3x-6y+33=0 pour équation cartésienne.
METHODE N°2 :
Déterminer par le calcul une équation cartésienne de la droite D qui passe par A (5;3) et B (-1;6) .
Il s’agit de déterminer une relation du type ax+by+c=0.
On calcule les coordonnées du vecteur \overrightarrow{AB}
On n’hésite pas à repérer les coordonnées des points A et B ainsi
\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}
\hspace{0.2cm} A(5;3) \hspace{0.4cm} B(-1;6)
On calcule les coordonnées du vecteur \overrightarrow{AB} (x_{B}-x_{A};y_{B}-y_{A})
Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.
\hspace{4.5cm}\overrightarrow{AB} ((-1)-5;6-3) \hspace{4.5cm}\overrightarrow{AB} (-6;3)le vecteur \overrightarrow{AB} (-6;3) est un vecteur directeur de D .
On sait , d’après le cours , que le vecteur de coordonnées (-b;a) est un vecteur directeur de la droite D d’équation ax+by+c=0 .
Donc ici -b=-6 et a=3.
Ou encore b=6 et a=3.
Donc une équation cartésienne de D est de la forme 3x+6y+c=0.
Pour déterminer c, il suffit de remplacer x et y par les coordonnées du point A c’est-à-dire 5 et 3.
{3}\times{5}+{6}\times{3}+c=0On résout l’équation dont l’inconnue est c.
15+18+c=0\\33+c=0\\c=-33Une équation de la droite D est 3x+6y-33=0.
Remarque avec la méthode n°1, on obtient –3x-6y+33=0. Il s’agit bien sûr de la même droite D qui possède plusieurs équations cartésiennes qui se déduisent toutes les unes des autres en multipliant par un nombre ici -1.
Vérification à l’aide de Géogébra.
Placer le point A
Cliquer sur le deuxième onglet en haut à droite et sélectionner Point dans le menu déroulant. Cliquer dans le repère sur le point de coordonnées (5;3).
Placer le point B
Cliquer sur le deuxième onglet en haut à droite et sélectionner Point dans le menu déroulant. Cliquer dans le repère sur le point de coordonnées (-1;6).
Tracer la droite (AB)
Cliquer sur le troisième onglet en haut à droite et sélectionner Droite dans le menu déroulant. Cliquer dans le repère sur les points A et B. Une équation de la droite (AB) apparaît dans la colonne de gauche, cliquer droit sur l’équation et choisir l’équation ax+by+c=0.



