Exercice : Session 15 Mars 2021 Sujet 1
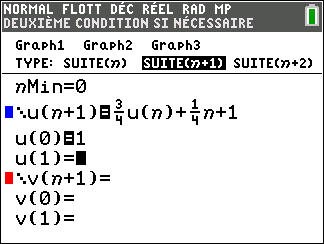
Soit (u_n) la suite définie sur \mathbf{N} par u_0=1 et u_{n+1}=\frac{3}{4}u_n+\frac{1}{4}n+1.
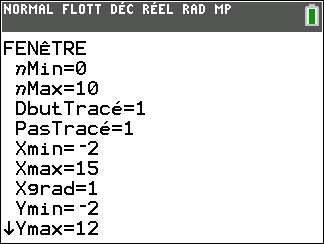
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
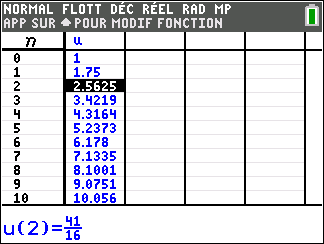
1. Calculer, en détaillant les calculs, u_1 et u_2.
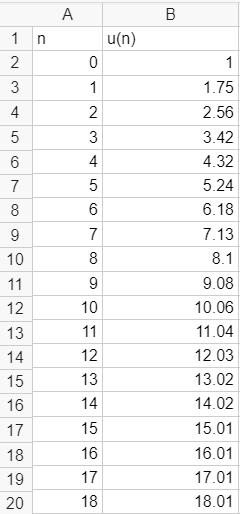
2.a. Quelle valeur doit-on saisir dans la cellule B2 et quelle formule, étirée ensuite vers le bas, doit-on écrire dans la cellule B3 de la feuille de calcul Géogébra ci-dessous pour obtenir les termes successifs de la suite (u_n) dans la colonne B ?
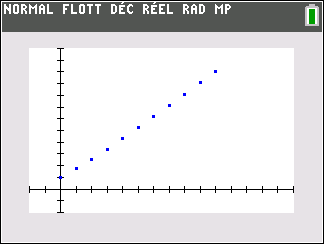
2.b. Conjecturer le sens de variation de la suite (u_n).
3. a. Démontrer par récurrence que, pour tout entier naturel n, on a : n\leq u_n\leq n+1.
3.b. En déduire, en justifiant la réponse, le sens de variation et la limite de la suite (u_n).
3.c. Démontrer que : lim_{n\to+\infty}\frac{u_n}{n}=1
4. On désigne par (v_n) la suite définie sur \mathbf{N} par v_n=u_n-n
a. Démontrer que la suite (v_n) est géométrique de raison \frac{3}{4}.
b. En déduire que, pour tout entier naturel n,on a : u_n=(\frac{3}{4})^n+n