Table des matières
Pour s’y retrouver dans les tirages
On tire k objets parmi les n objets d’un ensemble E.
Tirage successif (l’ordre compte)
Tirage simultané (l’ordre ne compte pas)
Avec remise
Les résultats sont des k-uplets, c’est-à-dire des listes ordonnées de k éléments de E (distincts ou non). Il y en a en tout
n^k
Il n’y a pas de tirage simultané avec remise.
Sans remise
Les résultats sont des k-uplets d’éléments distincts, c’est-à-dire des listes ordonnées de k éléments distincts de E ( dans des exercices anciens, on utilise le mot arrangement).
Il y en a en tout
n\times(n-1)\times…\times(n-k+1)
ou
\frac{n!}{(n-k)!}
Cas particulier : quand k=n, il s’agit de permutations de n objets et il y en a
n!
Les résultats sont des combinaisons de k d’éléments de E, c’est-à-dire des parties de k éléments de E. Il y en a
\binom{n}{k}
Combinaisons.
Exercice n°1
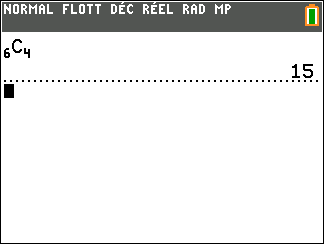
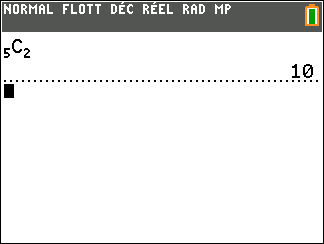
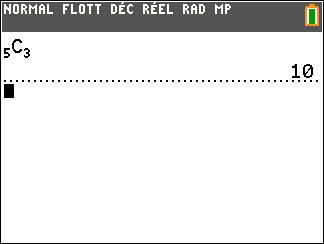
On tire simultanément deux boules dans une urne qui contient cinq boules numérotées de 1 à 5.
Combien y’a-t-il de tirages possibles ?
Exercice n°2
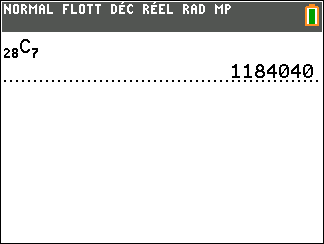
Un jeu de dominos contient 28 pièces. On tire sept dominos en début de partie.
Combien y’a-t-il de tirages de sept dominos possibles ?
Exercice n°3
Pour jouer à LOTO®, il vous suffit de cocher 6 numéros : 5 numéros sur une grille de 49 numéros et 1 numéro chance sur une grille de 10 numéros.
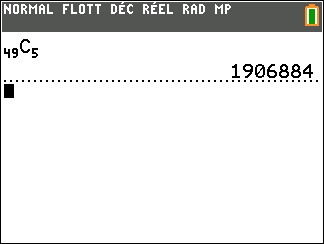
- Combien y’a-t-il de façons de cocher 5 numéros sur une grille de 49 numéros ?
2. Combien y’a-t-il de façons de cocher 1 numéro sur une grille de 10 numéros ?
3. En déduire le nombre de toutes les grilles qu’on peut former au loto.
Exercice n°4
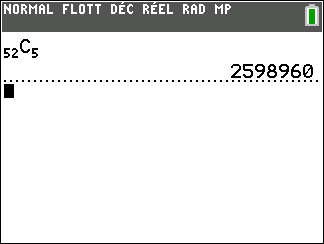
Pour jouer au poker, on utilise un jeu de 52 cartes. Une main est un ensemble de 5 cartes différentes.
- Combien y’a-t-il de mains différentes?
2. Une quinte flush est une main de cinq cartes de la même famille qui se suivent.
par exemple : \{as\heartsuit,roi\heartsuit,dame\heartsuit,valet\heartsuit,10\heartsuit \}
Combien y’a-t-il de quintes flush à coeur ?
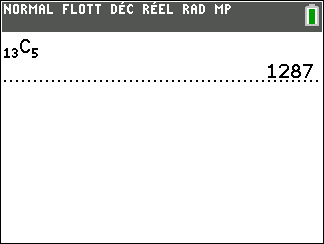
3. Une couleur est une main de 5 cartes de la même famille qui ne se suivent pas, si elles se suivent c’est une quinte flush.
Combien y’a-t-il de couleurs à coeur ?
Exercice n°5
Un sac contient 5 jetons verts (numérotés de 1 à 5) et 4 jetons rouges (numérotés de 1 à 4).
On tire simultanément et au hasard 3 jetons du sac.
1. Combien y’a-t-il de tirages différents au total ?
2. Combien y’a-t-il de tirages comportant 3 jetons verts ?
3. Combien y’a-t-il de tirages comportant au moins un jeton rouge ?
4. Combien y’a-t-il de tirages comportant exactement un jeton vert ?
Exercice n°6
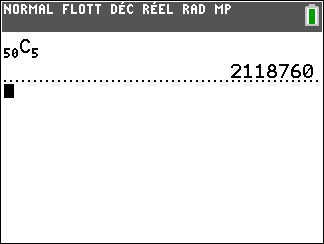
On sélectionne 5 personnes parmi 20 femmes et 30 hommes pour former une équipe.
1) De combien de façons peut-on constituer cette équipe de 5 personnes ?
2) Dans chacun des cas suivants, de combien de façons peut-on former cette équipe :
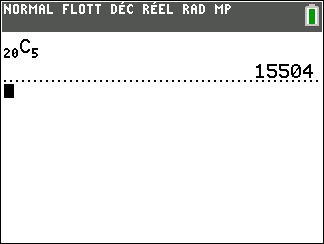
a) En ne sélectionnant que des femmes.
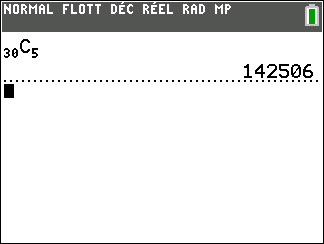
b) En ne sélectionnant que des personnes de même sexe.
c) En sélectionnant au moins une femme et au moins un homme.
Exercice n°7
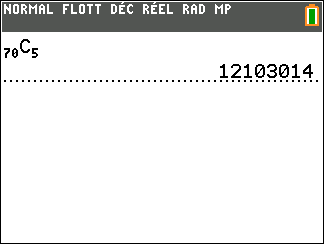
Dans un lycée, on compte 22 célibataires parmi les 70 professeurs. On désire faire un sondage : pour cela on choisit un échantillon de cinq personnes parmi les professeurs du lycée.
1) Quel est le nombre d’échantillons différents possibles ?
2) Quel est le nombre d’échantillons ne contenant aucun célibataire ?
3) Quel est le nombre d’échantillons contenant au moins un célibataire ?
Exercice n°8
Louis et Pierre sont membres d’un club de pétanque qui compte 15 personnes. Parmi ces 15 personnes, 3 doivent représenter le club au forum des associations.
1) Combien de groupes de 3 personnes peut-on constituer ?
2) Dans combien de ces groupes peut figurer Louis ?
3) Combien de groupes peut-on former de telle sorte que Louis et Pierre ne s’y retrouvent pas ensemble ?