Formules d’addition
Propriétés : formules d’addition
Pour tous réels a et b ,
cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
Exemple n°1
on se propose de calculer cos(\frac{\pi}{12}) et sin(\frac{\pi}{12}).
- Calculer \frac{\pi}{3}-\frac{\pi}{4}
\frac{\pi}{3}-\frac{\pi}{4}=\frac{\pi}{3}\times \frac{4}{4}-\frac{\pi}{4}\times \frac{3}{3}\\\frac{\pi}{3}-\frac{\pi}{4}=\frac{4\pi}{12}-\frac{3\pi}{12}\\\frac{\pi}{3}-\frac{\pi}{4}=\frac{\pi}{12}
2. En déduire
a. cos(\frac{\pi}{12})\\cos(\frac{\pi}{12})=cos(\frac{\pi}{3}-\frac{\pi}{4})
On remplace a par \frac{\pi}{3} et b par \frac{\pi}{4} dans cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
cos(\frac{\pi}{12})=cos(\frac{\pi}{3})cos(\frac{\pi}{4})+sin(\frac{\pi}{3})sin(\frac{\pi}{4})
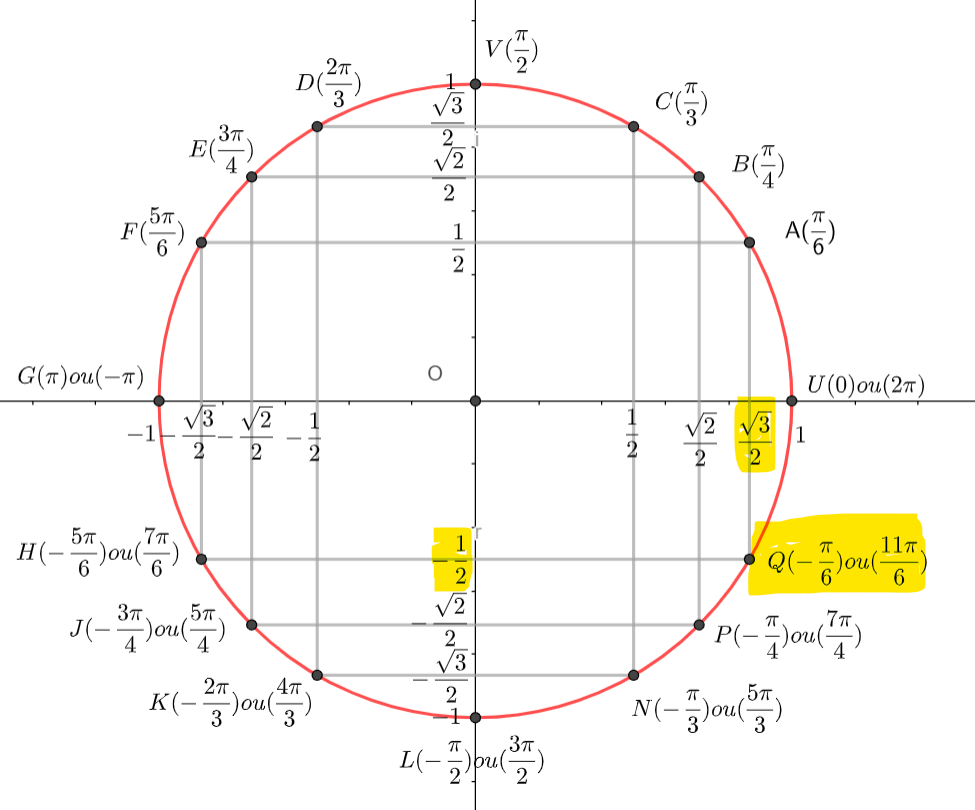
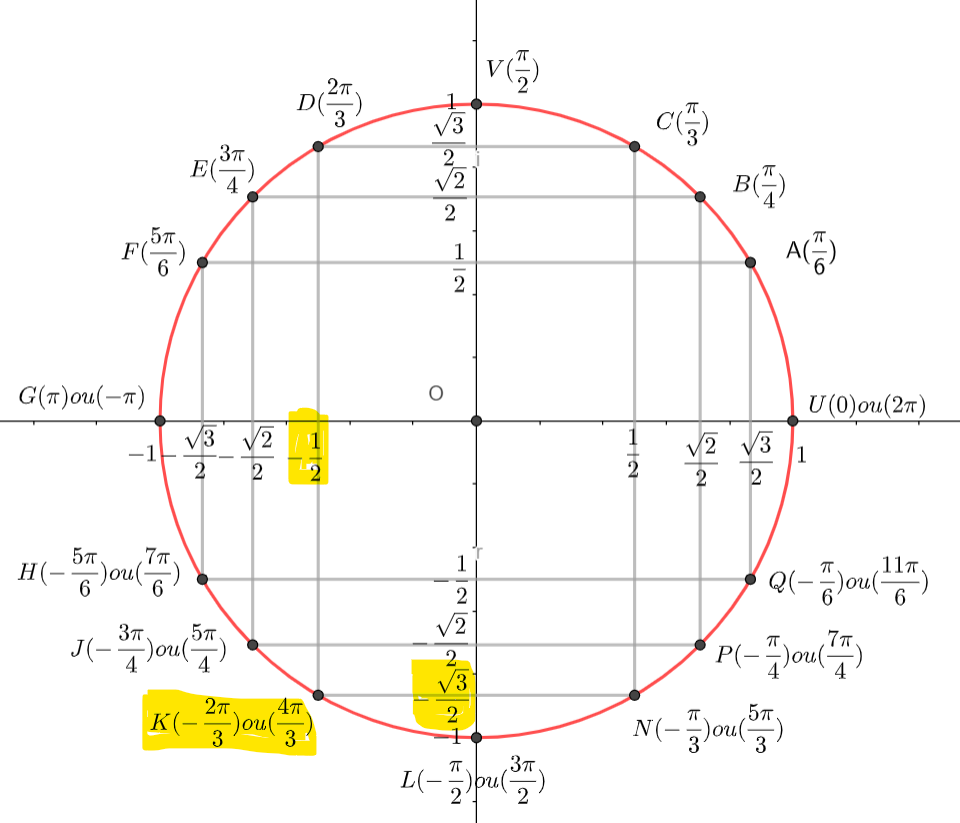
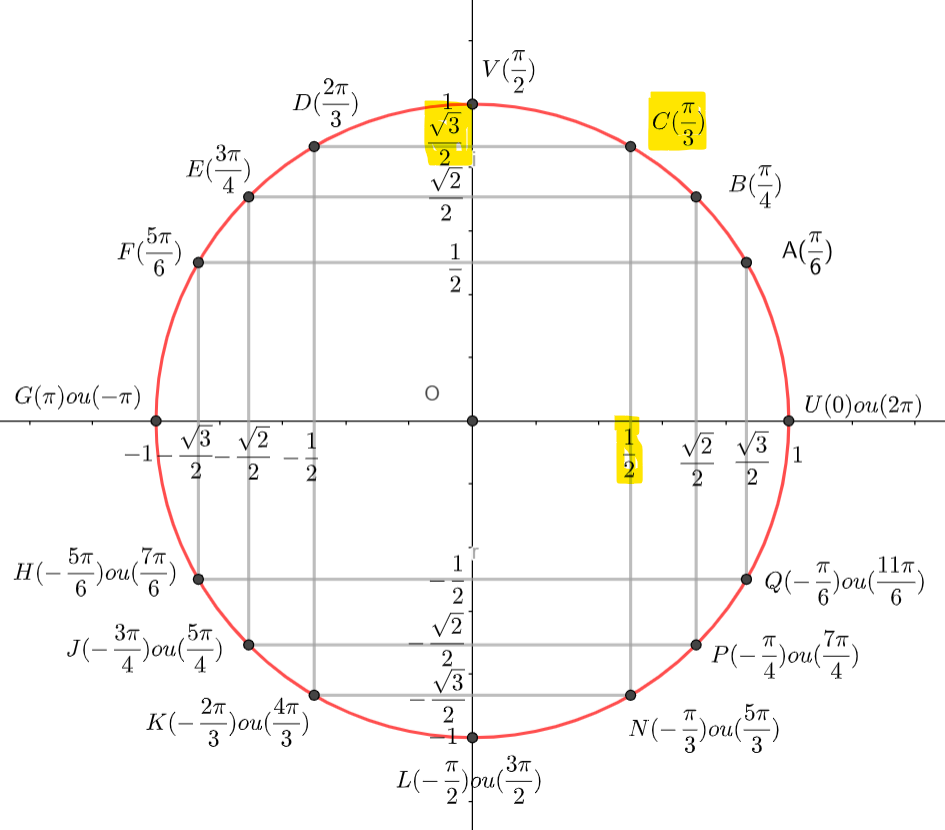
On utilise le tableau suivant pour poursuivre le calcul
cos(\frac{\pi}{12})=\frac{1}{2}\times \frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\times \frac{\sqrt{2}}{2}
cos(\frac{\pi}{12})= \frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}
cos(\frac{\pi}{12})= \frac{\sqrt{2}+\sqrt{6}}{4}
b. sin(\frac{\pi}{12})\\sin(\frac{\pi}{12})=sin(\frac{\pi}{3}-\frac{\pi}{4})
On remplace a par \frac{\pi}{3} et b par \frac{\pi}{4} dans sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
sin(\frac{\pi}{12})=sin(\frac{\pi}{3})cos(\frac{\pi}{4})-cos(\frac{\pi}{3})sin(\frac{\pi}{4})
On utilise le tableau suivant pour poursuivre le calcul
sin(\frac{\pi}{12})=\frac{\sqrt{3}}{2}\times \frac{\sqrt{2}}{2}-\frac{1}{2}\times \frac{\sqrt{2}}{2}
sin(\frac{\pi}{12})= \frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}
sin(\frac{\pi}{12})= \frac{\sqrt{6}-\sqrt{2}}{4}
Exercice n°1
on se propose de calculer cos(\frac{5\pi}{12}) et sin(\frac{5\pi}{12}).
- Calculer \frac{\pi}{6}+\frac{\pi}{4}
2. En déduire
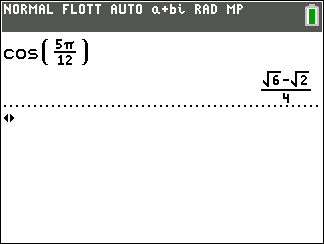
a. cos(\frac{5\pi}{12})
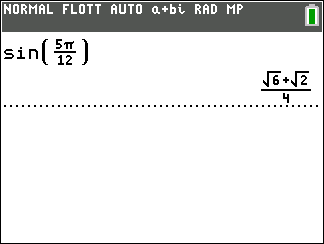
b. sin(\frac{5\pi}{12})
Exercice n°2
on se propose de calculer cos(\frac{7\pi}{12}) et sin(\frac{7\pi}{12}).
- Calculer \frac{\pi}{3}+\frac{\pi}{4}
2. En déduire
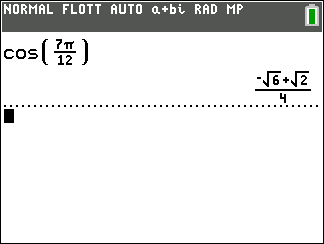
a. cos(\frac{7\pi}{12})
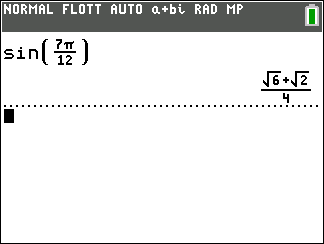
b. sin(\frac{7\pi}{12})
Formules de duplication
Propriété : formules de duplication
Pour tout réel a ,
cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)
sin(2a)=2sin(a)cos(a)
Exemple n°2
on se propose de calculer cos(\frac{\pi}{8}).
- Calculer 2\times \frac{\pi}{8}
2\times \frac{\pi}{8}=\frac{2\pi}{8}\\2\times \frac{\pi}{8}=\frac{\pi}{4}
2. En déduire cos(\frac{\pi}{8})\\cos(\frac{\pi}{4})=cos(2\times \frac{\pi}{8})
Dans le membre de droite, on utilise la propriété cos(2a)=2cos^2(a)-1 en remplaçant a par \frac{\pi}{8}.
cos(\frac{\pi}{4})=2cos^2(\frac{\pi}{8})-1
On écrit l’égalité dans l’autre sens.
2cos^2(\frac{\pi}{8})-1=cos(\frac{\pi}{4})\\2cos^2(\frac{\pi}{8})=cos(\frac{\pi}{4})+1
On utilise le tableau suivant pour poursuivre le calcul
2cos^2(\frac{\pi}{8})=\frac{\sqrt{2}}{2}+1\\2cos^2(\frac{\pi}{8})=\frac{\sqrt{2}}{2}+\frac{2}{2}\\2cos^2(\frac{\pi}{8})=\frac{\sqrt{2}+2}{2}\\cos^2(\frac{\pi}{8})=\frac{\sqrt{2}+2}{4}
Comme cos(\frac{\pi}{8}) est positif,
cos(\frac{\pi}{8})=\frac{\sqrt{\sqrt{2}+2}}{2}
Exercice n°3
on se propose de calculer cos(\frac{\pi}{12}).
- Calculer 2\times\frac{\pi}{12}
2. En déduire cos(\frac{\pi}{12})
Exercice n°4
On admet que cos(\frac{\pi}{5})=\frac{1+\sqrt{5}}{4}. Calculer cos(\frac{2\pi}{5}).
Argument et opérations
Propriétés : argument et opérations
Soient z et z' deux complexes non nuls,
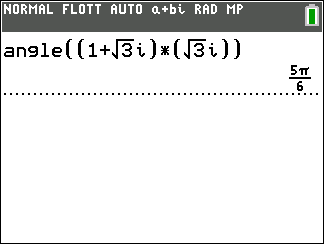
arg(z\times z')=arg(z)+arg(z')[2\pi]
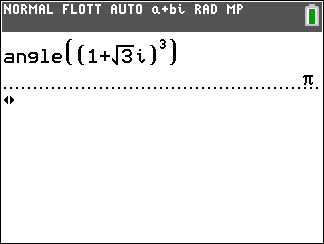
Pout tout entier naturel n , arg(z^n)=n\times arg(z)[2\pi]
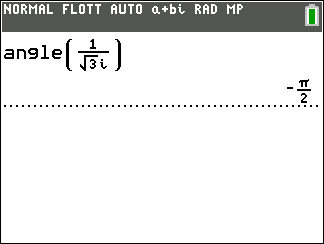
arg(\frac{1}{z})=-arg(z)[2\pi]
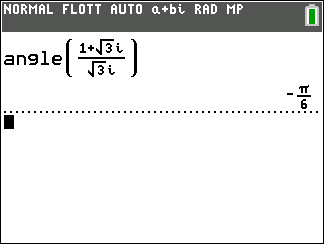
arg(\frac{z'}{z})=arg(z')-arg(z)[2\pi]
Exercice n°5
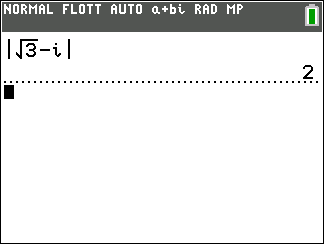
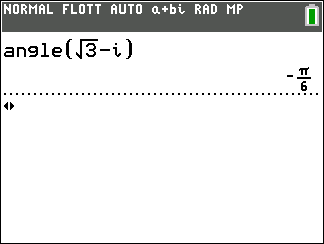
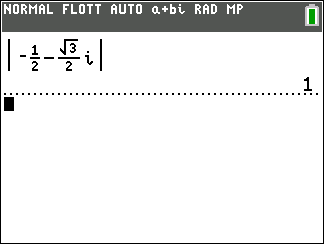
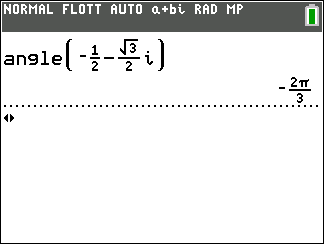
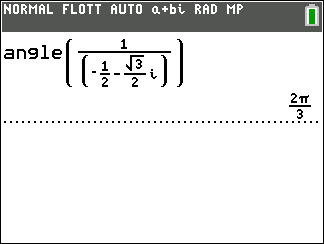
z_1=\sqrt{3}-i et z_2=-\frac{1}{2}-\frac{\sqrt{3}}{2}.
- Déterminer un argument de z_1 et de z_2
2. En déduire un argument dans chaque cas.
z_1\times z_2
z_1^6
\frac{1}{z_2}
\frac{z_1}{z_2}.
Exercice n°6
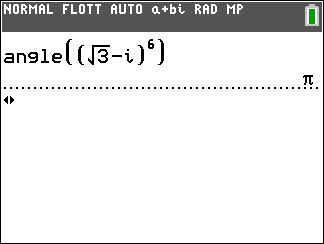
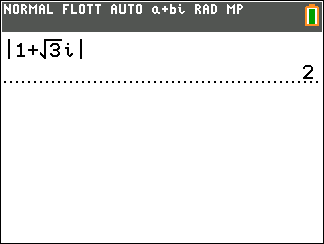
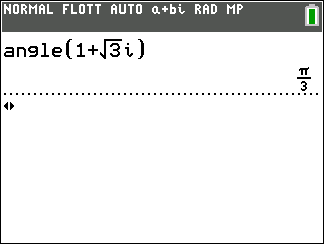
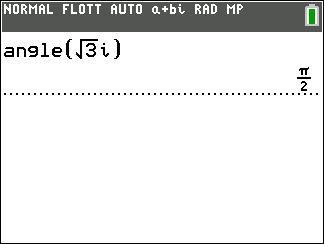
z_1=1+i\sqrt{3} et z_2=\sqrt{3}i.
- Déterminer un argument de z_1 et de z_2
2. En déduire un argument dans chaque cas.
z_1\times z_2
z_1^{3}
\frac{1}{z_2}
\frac{z_1}{z_2}.
Exercice n°7
Montrer que (3-3i)^{2408} est réel.