logo

TE. Complexes et géométrie : forme exponentielle.

Sommaire

Définition : forme exponentielle d’un nombre complexe

Définition

Tout nombre complexe non nul s’écrit sous la forme z=re^{i\theta} où r est le module de z et \theta un argument de z.

Cette écriture est appelée forme exponentielle de  z.

Exemple n°1

Soit le complexe 2+2i. On a |2+2i|=2\sqrt{2} et arg(2+2i)=\frac{\pi}{4} donc 2+2i=2\sqrt{2}e^{i\frac{\pi}{4}}.

Exemple n°2

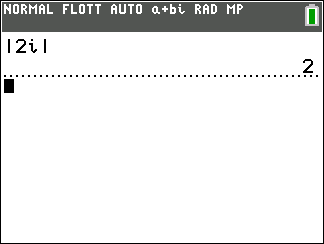
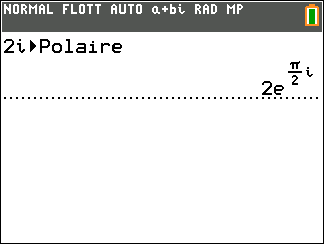
Soit le complexe i. On a |i|=1 et arg(i)=\frac{\pi}{2} donc i=e^{i\frac{\pi}{2}}.

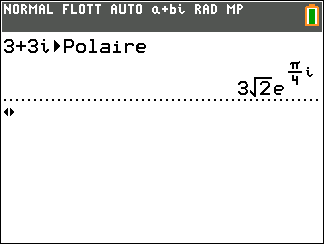
Exercice n°1 

Déterminer dans chaque cas le forme exponentielle de z.

z=-2-2\sqrt{3}i
correction
Je vérifie avec ma TI 83 Premium CE
z=3+3i
correction
Je vérifie avec ma TI 83 Premium CE
z=2i
correction
Je vérifie avec ma TI 83 Premium CE

Propriétés : calculs avec la forme exponentielle d’un nombre complexe

Propriétés

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

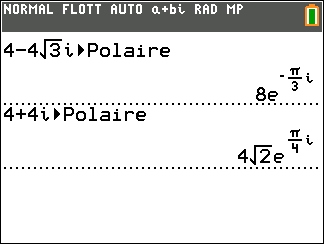
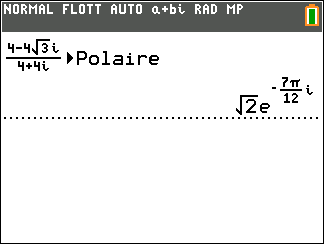
Exercice n°2

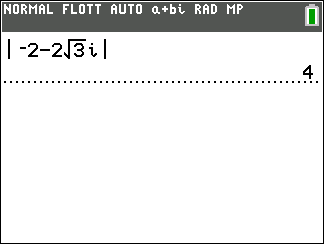
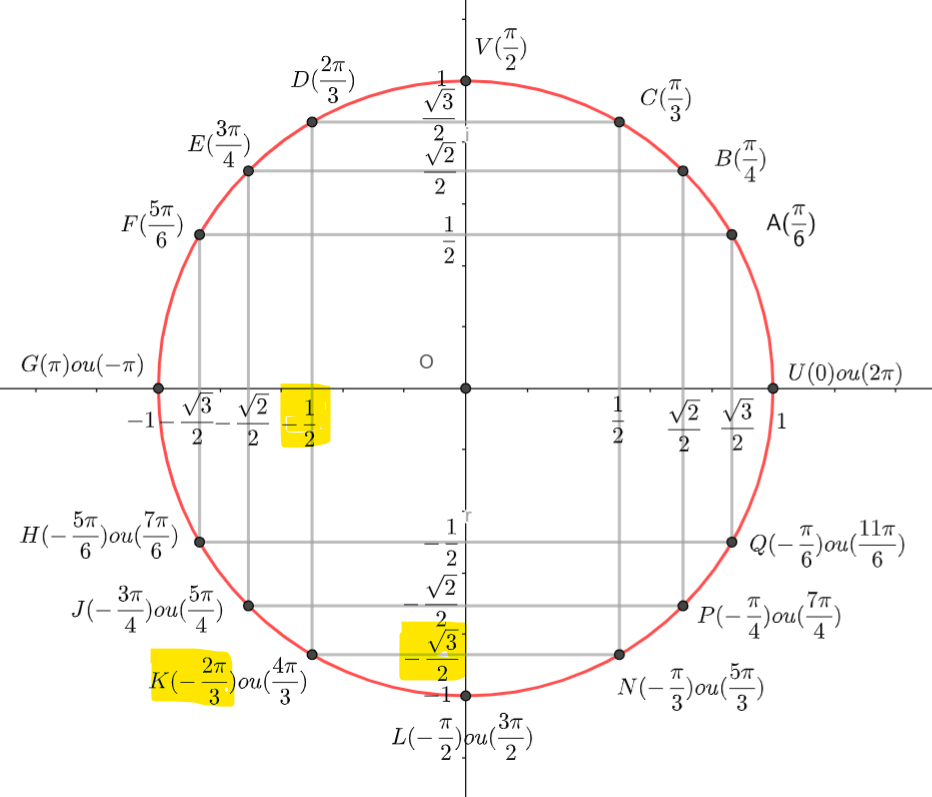
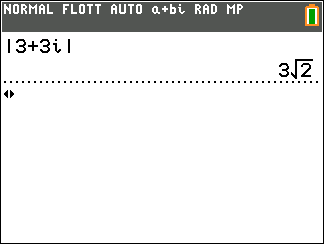
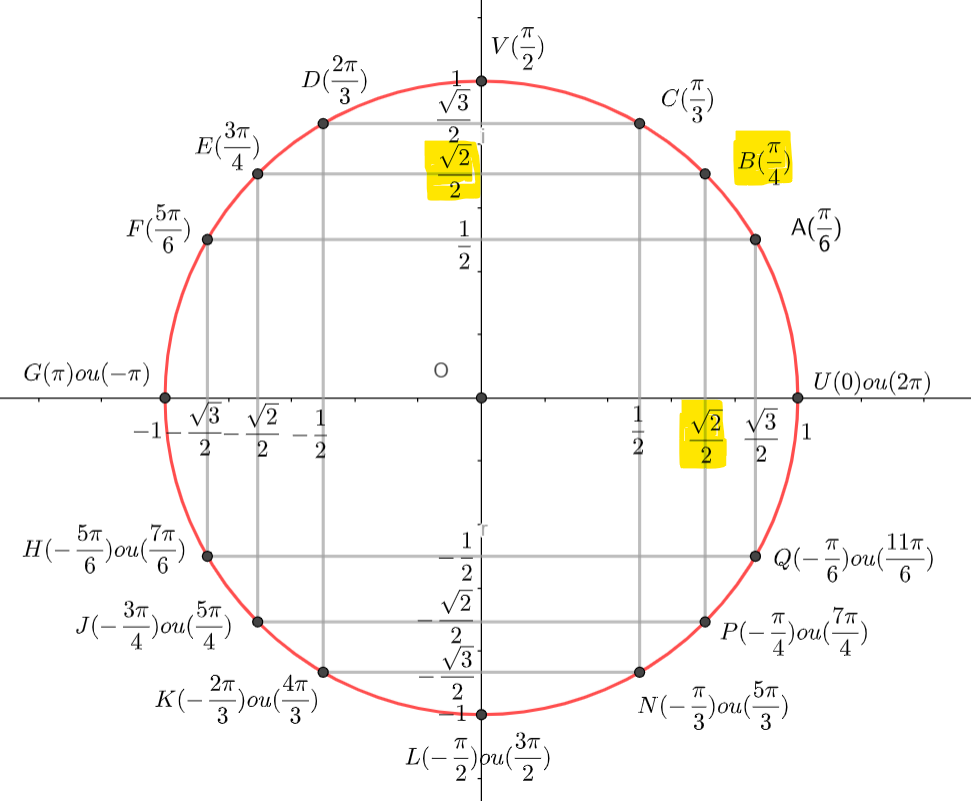
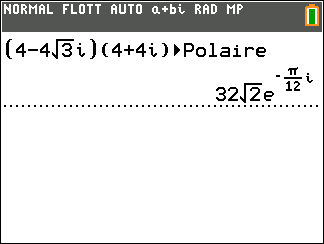
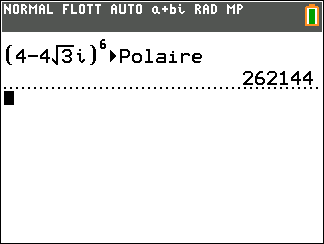
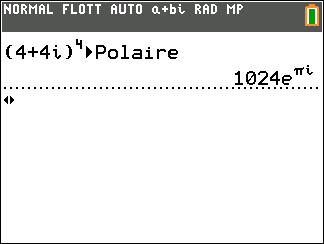
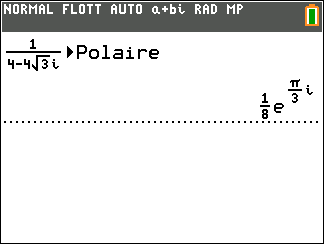
  1. A l’aide de la calculatrice, déterminer la forme exponentielle de z_1=4-4\sqrt{3}i et de z_2=4+4i
J'utilise ma TI 83 Premium CE

2. En utilisant les propriétés précédentes, déterminer la forme exponentielle dans chaque cas.

z_1\times z_2
correction
Je vérifie avec ma TI 83 Premium CE
z_1^6
correction
Je vérifie avec ma TI 83 Premium CE
z_2^4
correction
Je vérifie avec ma TI 83 Premium CE
\frac{1}{z_1}
correction
Je vérifie avec ma TI 83 Premium CE
\frac{1}{z_2}
correction
Je vérifie avec ma TI 83 Premium CE
\frac{z_1}{z_2}
correction
Je vérifie avec ma TI 83 Premium CE

Egalité de nombres complexes

Théorème 

Soient z=re^{i\Theta} et z’=r’e^{i\Theta’} deux nombres complexes sous forme exponentielle.

z=z’ \iff r=r’ et \theta=\theta'[2\pi]

Formule de Moivre

Théorème 

Pour tout \theta \in \mathbf{R} et pour tout n \in \mathbf{Z} , 

 (cos(\theta)+isin(\theta))^n=cos(n\theta)+isin(n\theta)

Formules d’Euler

Théorème 

Pour tout \theta \in \mathbf{R}  

 cos(\theta)=\frac{1}{2}(e^{i\theta}+e^{-i\theta}) et  sin(\theta)=\frac{1}{2i}(e^{i\theta}-e^{-i\theta})

Exercice n°3

Démontrer que pout tout réel x ,  cos(2x)sin^2(x)=-\frac{1}{4}cos(4x)+\frac{1}{2}cos(2x)-\frac{1}{4}

correction

Exercice n°4

Démontrer que pout tout réel x ,  sin(x)cos^2(x)=\frac{sin(3x)+sin(x)}{4}

correction

Exercice n°5

Démontrer que pout tout réel x ,  cos^3(x)=\frac{cos(3x)+3cos(x)}{4}

correction

©2020 – Math’O karé SAS

On veut écrire z=-2-2\sqrt{3}i sous forme exponentielle.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut -2 et b par la partie imaginaire de z qui vaut -2\sqrt{3} dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{(-2)^2+(-2\sqrt{3})^2}

\hspace{0.5cm}=\sqrt{4+(-2)^2\times(\sqrt{3})^2}

\hspace{0.5cm}=\sqrt{4+4\times 3}

\hspace{0.5cm}=\sqrt{16}

\hspace{0.5cm}=4

On peut vérifier avec la TI 83 Premium CE

2. On cherche un réel \theta tel que 

cos(\theta)=\frac{a}{|z|} et sin(\theta)=\frac{b}{|z|}

On remplace a par la partie rélle de z qui vaut -2 et b par la partie imaginaire de z qui vaut -2\sqrt{3} et |z| par 4 dans 

cos(\theta)=\frac{a}{|z|} et sin(\theta)=\frac{b}{|z|}.

cos(\theta)=-\frac{2}{4} et sin(\theta)=-\frac{2\sqrt{3}}{4}

Pour déterminer, par le calcul, une valeur de \theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\theta)=-\frac{2}{4}=-\frac{1}{2}

\Theta=cos^{-1}(-\frac{1}{2})

La  calculatrice donne \theta=\frac{2\pi}{3}

En réalité on obtient :

\theta=\frac{2\pi}{3} ou \theta=-\frac{2\pi}{3}

sin(\theta)=\frac{-2\sqrt{3}}{4}=-\frac{\sqrt{3}}{2}

\theta=sin^{-1}(-\frac{\sqrt{3}}{2})

La  calculatrice donne \theta=-\frac{\pi}{3}

En réalité on obtient :

\theta=-\frac{\pi}{3} ou \theta=\pi-(-\frac{\pi}{3})=\frac{4\pi}{3}=-\frac{2\pi}{3}[2\pi]

La solution commune aux deux équations est : \theta=-\frac{2\pi}{3}.

Donc arg(z)=-\frac{2\pi}{3}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place -\frac{1}{2} sur l’axe des abscisses, -\frac{\sqrt{3}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici -\frac{2\pi}{3}. attention il y a une infinité de mesures : -\frac{2\pi}{3}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=-\frac{2\pi}{3}[2\pi].

3. On en déduit la forme exponentielle

z=4e^{-i\frac{2\pi}{3}}

 

On veut écrire z=3+3i sous forme exponentielle.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut 3 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{3^2+3^2}

\hspace{0.5cm}=\sqrt{9+9}

\hspace{0.5cm}=\sqrt{18}

\hspace{0.5cm}=\sqrt{9\times 2}

\hspace{0.5cm}=\sqrt{9}\times \sqrt{2}

\hspace{0.5cm}=3\sqrt{2}

On peut vérifier avec la TI 83 Premium CE

2. On remplace a par la partie rélle de z qui vaut 3 et b par la partie imaginaire de z qui vaut 3 et |z| par 3\sqrt{2} dans 

cos(\theta)=\frac{a}{|z|} et sin(\theta)=\frac{b}{|z|}.

cos(\theta)=\frac{3}{3\sqrt{2}} et sin(\theta)=\frac{3}{3\sqrt{2}}\\cos(\theta)=\frac{1}{\sqrt{2}} et sin(\theta)=\frac{1}{\sqrt{2}}\\cos(\theta)=\frac{\sqrt{2}}{2} et sin(\theta)=\frac{\sqrt{2}}{2}

Pour déterminer, par le calcul, une valeur de \theta, il y a plusieurs méthodes :

méthode n°1 : on utilise les touches cos^{-1} et sin^{-1} de la calculatrice.

cos(\theta)=\frac{\sqrt{2}}{2}

\theta=cos^{-1}(\frac{\sqrt{2}}{2})

La  calculatrice donne \theta=\frac{\pi}{4}

En réalité on obtient :

\theta=\frac{\pi}{4} ou \theta=-\frac{\pi}{4}

sin(\theta)=\frac{\sqrt{2}}{2}

\theta=sin^{-1}(\frac{\sqrt{2}}{2})

La  calculatrice donne \theta=\frac{\pi}{4}

En réalité on obtient :

\theta=\frac{\pi}{4} ou \theta=\pi-(\frac{\pi}{4})

La solution commune aux deux équations est : \theta=\frac{\pi}{4}.

Donc arg(z)=\frac{\pi}{4}[2\pi].

méthode n°2 : on utilise le cercle trigonométrique ci-dessous 

On place \frac{\sqrt{2}}{2} sur l’axe des abscisses, \frac{\sqrt{2}}{2} sur l’axe des ordonnées et on lit l’angle correspondant, ici \frac{\pi}{4}. attention il y a une infinité de mesures : \frac{\pi}{4}+2k\pi.

A l’aide du cercle trigonométrique, on obtient :  arg(z)=\frac{\pi}{4}[2\pi].

3. On en déduit la forme exponentielle

z=3\sqrt{2}e^{i\frac{\pi}{4}}

 

 

On veut écrire z=2i sous forme trigonométrique.

1.On calcule le module de z

On remplace a par la partie rélle de z qui vaut 0 et b par la partie imaginaire de z qui vaut 2 dans 

|z|=\sqrt{a^2+b^2}.

|z|=\sqrt{0^2+2^2}

\hspace{0.5cm}=\sqrt{0+4}

\hspace{0.5cm}=\sqrt{4}

\hspace{0.5cm}=2

On peut vérifier avec la TI 83 Premium CE

2. On détermine l’argument de z=2i

Comme z=2i est un imaginaire avec une partie imaginaire positive, d’après les propriétés du cours,  on a :  arg(z)=\frac{\pi}{2}[2\pi].

3. On en déduit la forme exponentielle de  z=2i

z=2e^{i\frac{\pi}{2}}

 

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de z_1\times z_2.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

z_1\times z_2=8e^{-i\frac{\pi}{3}}\times 4\sqrt{2}e^{i\frac{\pi}{4}}\\\hspace{1.15cm}=8\times 4\sqrt{2}e^{i(-\frac{\pi}{3}+\frac{\pi}{4})}\\\hspace{1.15cm}=32\sqrt{2}e^{i(-\frac{\pi}{3}\times \frac{4}{4}+\frac{\pi}{4}\times \frac{3}{3})}\\\hspace{1.15cm}=32\sqrt{2}e^{i(-\frac{4\pi}{12}+\frac{3\pi}{12})}\\\hspace{1.15cm}=32\sqrt{2}e^{i(-\frac{\pi}{12})}

 

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de z_1^6.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

z_1^6=(8e^{-i\frac{\pi}{3}})^6\\\hspace{0.4cm}=8^6 e^{i6(-\frac{\pi}{3})}\\\hspace{0.4cm}=262144 e^{-2i\pi}

On peut éventuellement poursuivre

\hspace{0.4cm}=262144 \times 1\\\hspace{0.4cm}=262144

 

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de z_2^4.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

z_2^4=(4\sqrt{2}e^{i\frac{\pi}{4}})^4\\\hspace{0.4cm}=(4\sqrt{2})^4 e^{i4(\frac{\pi}{4})}\\\hspace{0.4cm}=1024 e^{i\pi}

 

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de \frac{1}{z_1}.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

\frac{1}{z_1}=\frac{1}{8e^{-i\frac{\pi}{3}}}\\\hspace{0.4cm}=\frac{1}{8}e^{-(-i\frac{\pi}{3})}\\\hspace{0.4cm}=\frac{1}{8}e^{i\frac{\pi}{3}}

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de \frac{1}{z_2}.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

\frac{1}{z_2}=\frac{1}{4\sqrt{2}e^{i\frac{\pi}{4}}}\\\hspace{0.4cm}=\frac{1}{4\sqrt{2}}e^{-i\frac{\pi}{4}}

On peut poursuivre

\hspace{0.4cm}=\frac{1}{4\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}} e^{-i\frac{\pi}{4}}\\\hspace{0.4cm}=\frac{\sqrt{2}}{4\sqrt{2}^2} e^{-i\frac{\pi}{4}}\\\hspace{0.4cm}=\frac{\sqrt{2}}{8} e^{-i\frac{\pi}{4}}

 

On a montré dans la question 1 que z_1=8e^{-i\frac{\pi}{3}} et  z_2=4\sqrt{2}e^{i\frac{\pi}{4}}.

On veut déterminer la forme exponentielle de \frac{z_1}{z_2}.

On utilise la formule en rouge.

Pour tous réels \theta et \theta’ , on a

re^{i\theta}\times r’e^{i\theta’}=rr’e^{i(\theta+\theta’)}

Pour tout n \in \mathbf{Z} , (re^{i\theta})^n=r^n e^{in\theta}

Pour tout k \in \mathbf{Z} , re^{i(\theta+2k\pi)}=re^{i\theta}

\frac{1}{re^{i\theta}}=\frac{1}{r}e^{-i\theta}=\overline{\frac{1}{r} e^{i\theta}}

\frac{re^{i\theta’}}{r’e^{i\theta}}=\frac{r}{r’}e^{i(\theta’-\theta)}

\frac{z_1}{z_2}=\frac{8e^{-i\frac{\pi}{3}}}{4\sqrt{2}e^{i\frac{\pi}{4}}}\\\hspace{0.4cm}=\frac{8}{4\sqrt{2}}e^{(-i\frac{\pi}{3}-i\frac{\pi}{4})}\\\hspace{0.4cm}=\frac{8}{4\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}e^{i(-\frac{\pi}{3}\times\frac{4}{4}-\frac{\pi}{4}\times\frac{3}{3})}\\\hspace{0.4cm}=\frac{8\sqrt{2}}{8}e^{i(-\frac{4\pi}{12}-\frac{3\pi}{12})}\\\hspace{0.4cm}=\sqrt{2}e^{-\frac{7\pi}{12}i}

 

 

On veut démontrer que pout tout réel x ,  cos(2x)sin^2(x)=-\frac{1}{4}cos(4x)+\frac{1}{2}cos(2x)-\frac{1}{4}.

On peut décider de montrer que les deux membres de l’égalité sont égaux à un même troisième.

On utilise les formules d’Euler, on remplace cos(2x) par \frac{e^{i2x}+e^{-i2x}}{2} et sin(x) par \frac{e^{ix}-e^{-ix}}{2i}

cos(2x)sin^2(x).

=\frac{e^{i2x}+e^{-i2x}}{2}\times (\frac{e^{ix}-e^{-ix}}{2i})^2.

On effectue la puissance , ici le carré.

=\frac{e^{i2x}+e^{-i2x}}{2}\times \frac{(e^{ix})^2-2(e^{ix})(e^{-ix})+(e^{-ix})^2}{4i^2}\\=\frac{e^{i2x}+e^{-i2x}}{2}\times \frac{e^{i2x}-2(e^{0})+(e^{-i2x})}{(-4)}\\=\frac{e^{i2x}+e^{-i2x}}{2}\times \frac{e^{i2x}-2+e^{-i2x}}{(-4)}\\= \frac{e^{i2x}e^{i2x}-e^{i2x}2+e^{i2x}e^{-i2x}+e^{-i2x}e^{i2x}-e^{-i2x}2+e^{-i2x}e^{-i2x}}{(-8)}\\=- \frac{e^{i4x}-2e^{i2x}+1+1-2e^{-i2x}+e^{-i4x}}{8}\\=- \frac{e^{i4x}-2e^{i2x}+2-2e^{-i2x}+e^{-i4x}}{8}\\= \frac{-e^{i4x}+2e^{i2x}-2+2e^{-i2x}-e^{-i4x}}{8}

On utilise les formules d’Euler, on remplace cos(4x) par \frac{e^{i4x}+e^{-i4x}}{2} et cos(2x) par \frac{e^{i2x}+e^{-i2x}}{2}

-\frac{1}{4}cos(4x)+\frac{1}{2}cos(2x)-\frac{1}{4}.

=-\frac{1}{4}\times \frac{e^{i4x}+e^{-i4x}}{2}+\frac{1}{2}\frac{e^{i2x}+e^{-i2x}}{2}-\frac{1}{4}\\=-\frac{1}{4}\times \frac{e^{i4x} +e^{-i4x}}{2}+\frac{1}{2}\frac{e^{i2x}+e^{-i2x}}{2}\times \frac{2}{2}-\frac{1}{4}\times \frac{2}{2}\\= \frac{-e^{i4x} -e^{-i4x}}{8}+\frac{2e^{i2x}+2e^{-i2x}}{8}-\frac{2}{8}\\= \frac{-e^{i4x} -e^{-i4x}+2e^{i2x}+2e^{-i2x}-2}{8}

Donc cos(2x)sin^2(x)=-\frac{1}{4}cos(4x)+\frac{1}{2}cos(2x)-\frac{1}{4}.

 

On veut démontrer que pout tout réel x,  sin(x)cos^2(x)=\frac{sin(3x)+sin(x)}{4}.

On peut décider de montrer que les deux membres de l’égalité sont égaux à un même troisième.

On utilise les formules d’Euler, on remplace cos(x) par \frac{e^{ix}+e^{-ix}}{2} et sin(x) par \frac{e^{ix}-e^{-ix}}{2i}

sin(x)cos^2(x).

=\frac{e^{ix}-e^{-ix}}{2i}\times (\frac{e^{ix}+e^{-ix}}{2})^2.

On effectue la puissance , ici le carré.

=\frac{e^{ix}-e^{-ix}}{2i}\times \frac{(e^{ix})^2+2(e^{ix})(e^{-ix})+(e^{-ix})^2}{4}\\=\frac{e^{ix}-e^{-ix}}{2i}\times \frac{e^{i2x}+2(e^{0})+(e^{-i2x})}{4}\\=\frac{e^{ix}-e^{-ix}}{2i}\times \frac{e^{i2x}+2+e^{-i2x}}{4}\\= \frac{e^{ix}e^{i2x}+e^{ix}2+e^{ix}e^{-i2x}-e^{-ix}e^{i2x}-e^{-ix}2-e^{-ix}e^{-i2x}}{8i}\\= \frac{e^{i3x}+2e^{ix}+e^{-ix}-e^{ix}-2e^{-ix}-e^{-i3x}}{8i}\\= \frac{e^{i3x}+e^{ix}-e^{-ix}-e^{-i3x}}{8i}

On utilise les formules d’Euler, on remplace sin(3x) par \frac{e^{i3x}-e^{-i3x}}{2i} et sin(x) par \frac{e^{ix}-e^{-ix}}{2i}

\frac{sin(3x)+sin(x)}{4}.

=\frac{\frac{e^{i3x}-e^{-i3x}}{2i}+\frac{e^{ix}-e^{-ix}}{2i}}{4}\\=\frac{\frac{e^{i3x}-e^{-i3x}+e^{ix}-e^{-ix}}{2i}}{4}\\=\frac{e^{i3x}-e^{-i3x}+e^{ix}-e^{-ix}}{8i}

Donc sin(x)cos^2(x)=\frac{sin(3x)+sin(x)}{4}.

 

 

On veut démontrer que pout tout réel x ,  cos^3(x)=\frac{cos(3x)+3cos(x)}{4}.

On peut décider de montrer que les deux membres de l’égalité sont égaux à un même troisième.

On utilise les formules d’Euler, on remplace cos(x) par \frac{e^{ix}+e^{-ix}}{2}.

cos(x)^3.

=(\frac{e^{ix}+e^{-ix}}{2})^3.

On effectue la puissance , ici le cube. 

=\frac{(e^{ix}+e^{-ix})^3}{2^3}

On utilise (a+b)^3=a^3+3a^2b+3ab^2+b^3.

=\frac{(e^{ix})^3+3(e^{ix})^2(e^{-ix})+3(e^{ix})(e^{-ix})^2+(e^{-ix})^3}{2^3}\\=\frac{e^{i3x}+3e^{i2x}e^{-ix}+3e^{ix}e^{-i2x}+e^{-i3x}}{8}\\=\frac{e^{i3x}+3e^{ix}+3e^{-ix}+e^{-i3x}}{8}

On utilise les formules d’Euler, on remplace cos(3x) par \frac{e^{i3x}+e^{-i3x}}{2} et cos(x) par \frac{e^{ix}+e^{-ix}}{2}

\frac{cos(3x)+3cos(x)}{4}.

=\frac{\frac{e^{i3x}+e^{-i3x}}{2}+3(\frac{e^{ix}+e^{-ix}}{2})}{4}.

=\frac{\frac{e^{i3x}+e^{-i3x}+3e^{ix}+3e^{-ix}}{2}}{4}\\=\frac{e^{i3x}+e^{-i3x}+3e^{ix}+3e^{-ix}}{8}

Donc cos^3(x)=\frac{cos(3x)+3cos(x)}{4}.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.