Sommaire
Existence et unicité d’une décomposition
Propriété
Tout entier naturel n\geq 2 est premier ou produit de nombres premiers.
Méthode n°1 : pour décomposer un nombre en produit de facteurs premiers par le calcul.
On se propose de décomposer 3150 en produit de facteurs premiers. Encore faut-il connaître les nombres premiers.
Voici les premiers 2,3,5,7,11,13,17,19,23,… .
Le plus simple est de diviser 3150 par 2 puis continuer à diviser par 2 si c’est possible, on passe ensuite à 3 et on continue jusqu’à temps de tomber sur 1.
Voici comment procéder :
3150
1575
525
175
35
7
1
2
3
3
5
5
7
On obtient alors la décomposition suivante : 3150=2\times3^2\times5^2\times7
Méthode n°2 : pour décomposer un nombre en produit de facteurs premiers avec Géogébra.
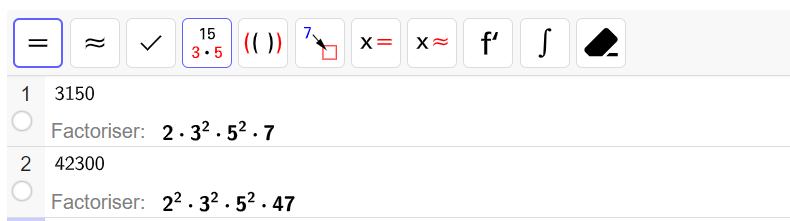
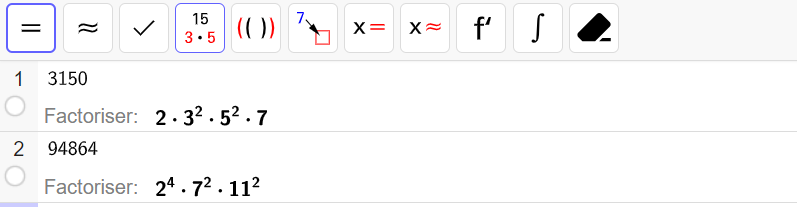
Saisir 3150 sur la ligne n°1.
Cliquer sur le quatrième onglet en haut à gauche, s’affiche alors Factoriser : 2.3^2.5^2.7.
Utiliser cette page active Géogébra pour vérifier les décompositions obtenues dans cet article.
Propriété
La décomposition en produit de facteurs premiers de tout entier naturel n\geq 2 est unique.
Exercice n°1
Décomposer les nombres suivants en produit de facteurs premiers. Utiliser la page Géogébra au-dessus pour conjecturer le résultat.
Exercice n°2
- Décomposer les nombres suivants en produit de facteurs premiers. Utiliser la page Géogébra au-dessus pour conjecturer le résultat.
2.a. En déduire une simplification de \frac{375}{165}
2.b. En déduire une factorisation de 375a+165b.
2.c. En déduire le PGCD de 375 et 165 .
Exercice n°3
- Décomposer les nombres suivants en produit de facteurs premiers. Utiliser la page Géogébra au-dessus pour conjecturer le résultat.
2.a. En déduire une simplification de \frac{1764}{504}
2.b. En déduire une factorisation de 1764a+504b.
2.c. En déduire le PGCD de 1764 et 504.
Diviseurs d’un entier naturel non premier
Propriété
Soit un entier n\geq 2 tel que n=p_1^{\alpha_1}p_2^{\alpha_2}p_3^{\alpha_3}…p_r^{\alpha_r} est premier ou produit de nombres premiers.
Les diviseurs positifs de n sont de la forme n=p_1^{{\alpha_1}’}p_2^{{\alpha_2}’}p_3^{{\alpha_3}’}…p_r^{\alpha_r’} avec 0\leq {\alpha_1}’\leq{\alpha_1} , 0\leq {\alpha_2}’\leq{\alpha_2} , 0\leq {\alpha_3}’\leq{\alpha_3} , … , 0\leq {\alpha_r}’\leq{\alpha_r}.
Méthode : pour déterminer tous les diviseurs d’un nombre entier naturel.
On se propose de déterminer tous les diviseurs de 98.
Etape n°1 : Décomposer 98 en produit de facteurs premiers
98
49
7
1
2
7
7
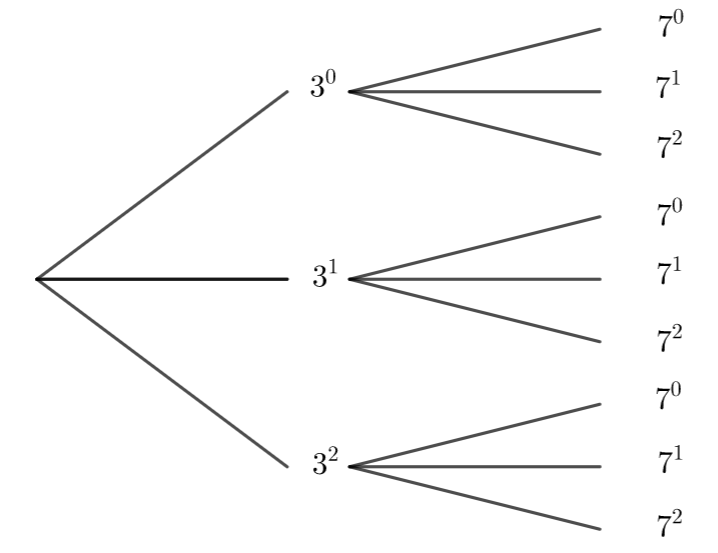
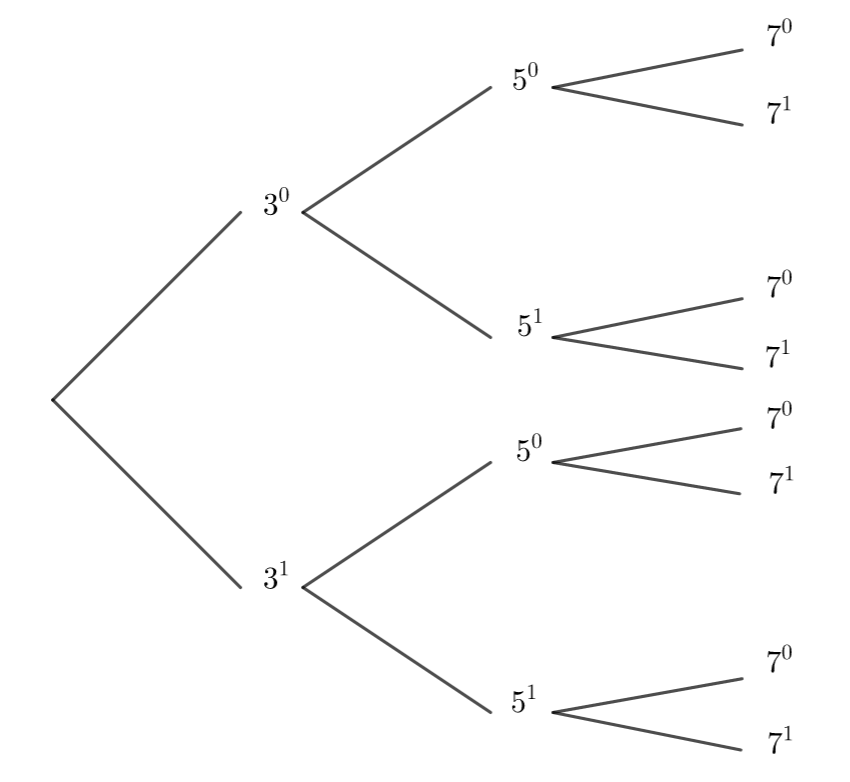
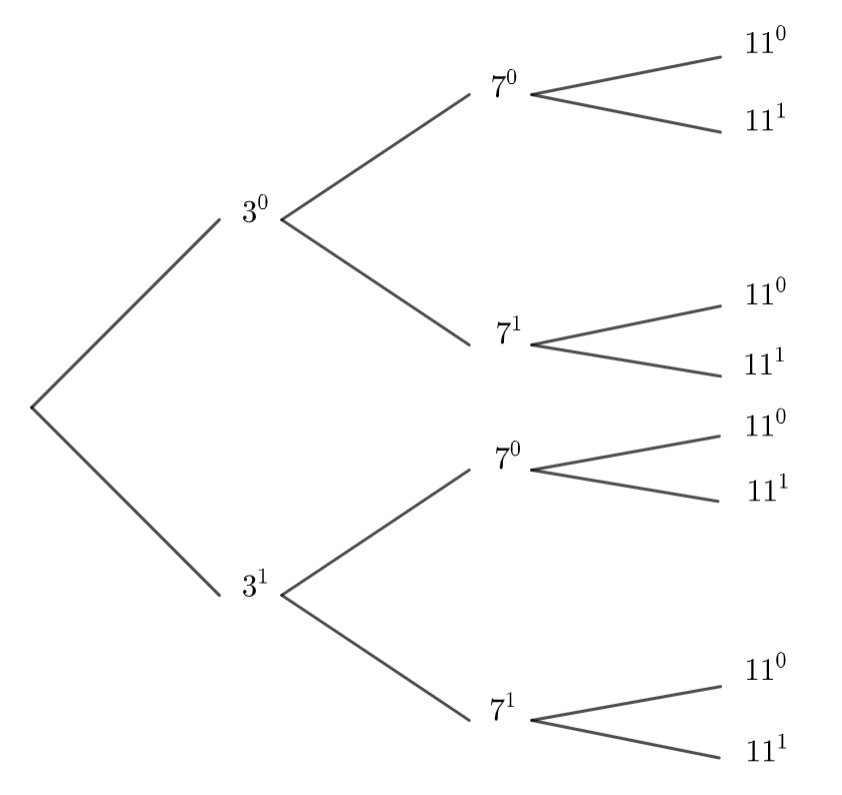
Etape n°2 : Représenter les diviseurs comme des chemins dans un arbre.
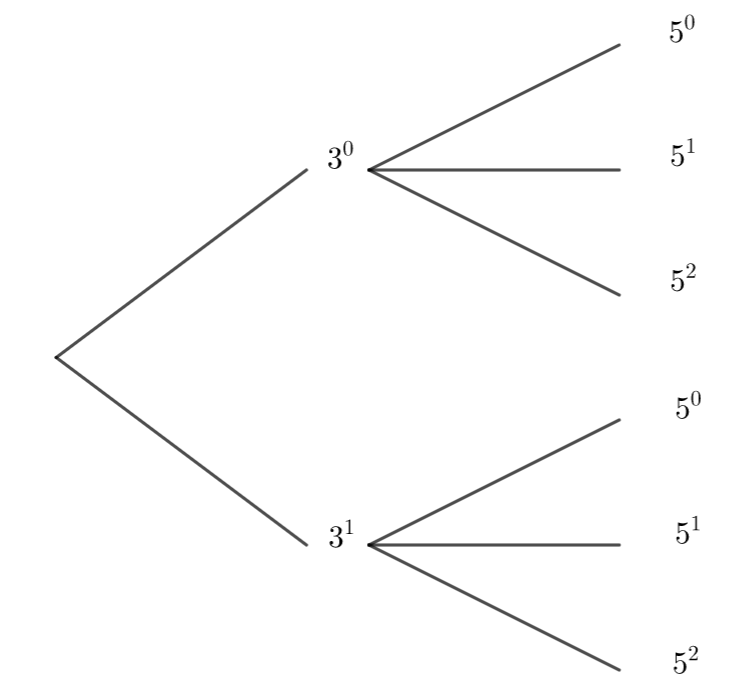
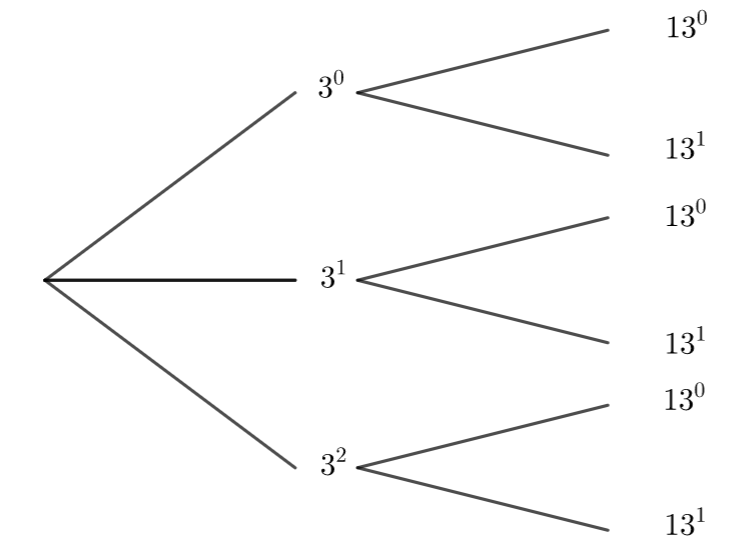
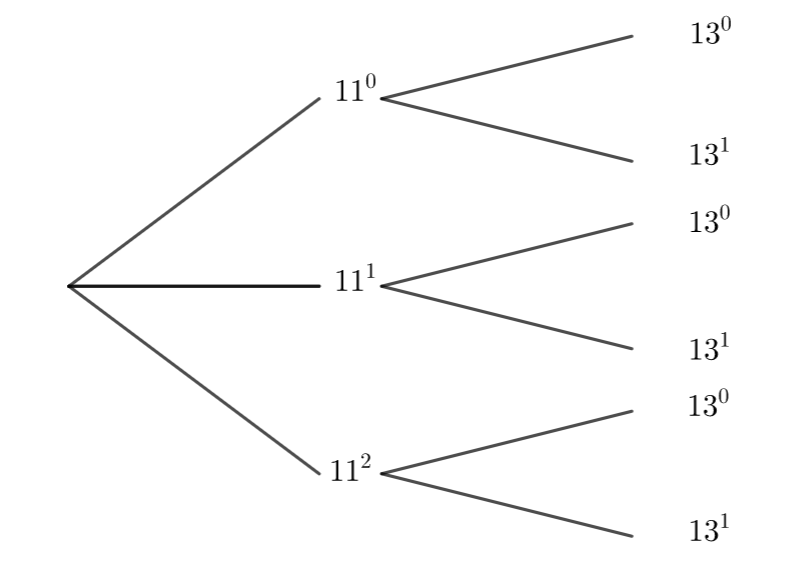
D’après la propriété, les diviseurs de 98=2\times 7^2 s’écrivent 2^{\alpha}\times 7^{\beta} avec 0\leq {\alpha}\leq 1 et 0\leq {\beta}\leq 2.
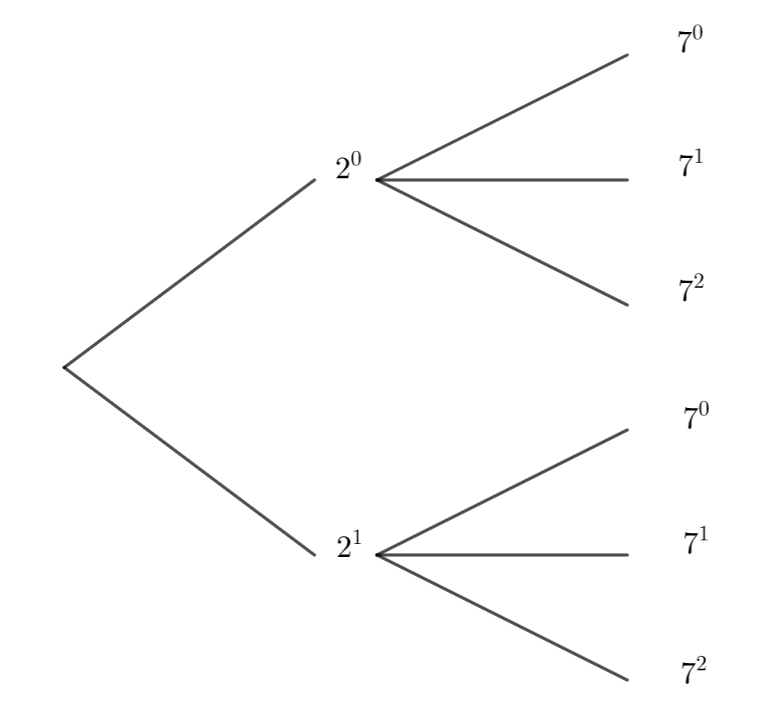
et 2^{1}\times 7^{2}=2\times 49=98
Les diviseurs de 98 sont : 1,2,7,14,49,98.
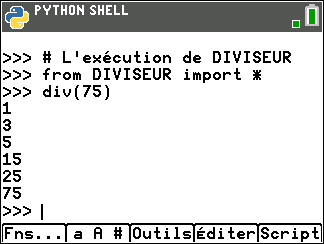
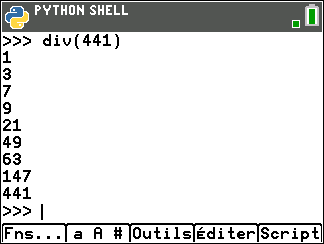
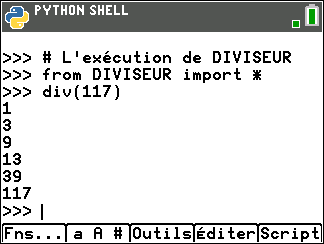
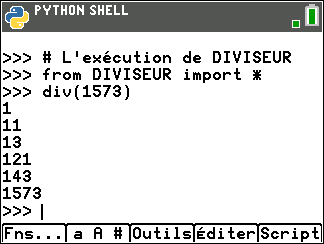
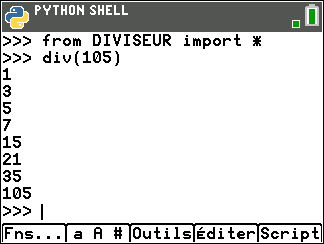
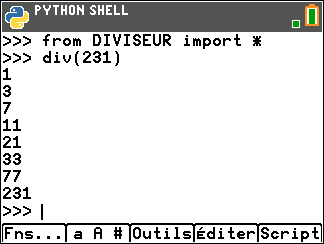
On peut vérifier le résultat en utilisant le programme DIVISEUR écrit en langage Python dans le niveau seconde du site MATH’O KARE
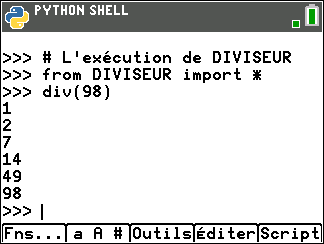
Pour ceux qui ne l’ont pas dans leur TI 83 Python, cliquer sur le bouton ci-dessous et écrire le programme.
Exercice n°4
Déterminer tous les diviseurs des nombres suivants
Exercice n°5
Utiliser la page Géogébra ci-dessus pour obtenir la décomposition en produit de facteurs premiers et déterminer le nombre de diviseurs positifs des nombres suivants sans les calculer.